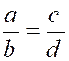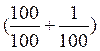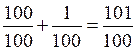|
|
|
|
Les suites et
ensembles de nombres |
ENVIRONNEMENT du dossier:
|
Cours sur le rapport
géométrique et sur les proportions géométriques ; |
DOSSIER
: Vocabulaire
et définitions d’expressions utilisées en mathématiques associées au mot
« géométrique »
A savoir :
· « Rapport
géométrique »
· Proportion géométrique.
· Suite géométrique
(découverte)
|
|
||
|
|
On appelle
« rapport géométrique » de « a » à « b » , ou simplement « rapport » de « a »
à « b » , l’expression « a : b » ou |
|
|
|
||
|
|
La dénomination de
« progression géométrique » vient de l’usage qu’ont fait de ces
proportions les géomètres de l’ Antiquité. EUCLIDE , il y a vingt trois
siècle ( 2012) , dans ses immortelles « Eléments de Géométrie »
, a donné une théorie des proportions d’une extrême profondeur et d’une
absolue rigueur. Il part de cette définition : « Quatre grandeurs
continues ( Euclide n’en considère pas d’autres) sont proportionnelles, si
entre ces quantités « a ; b ; c ; d », les relations
« Ma > Nb » et
« Mc>Nd » s’entraînent l’une l’autre
réciproquement , ou encore les relations « Ma = Nb » et « Mc =
Nd », ou enfin « Ma < Nb » et
« Mc <Nd » , « M » et
« N » étant des nombres quelconques. Quant à la notation ,
les Français adoptent la forme fractionnaire « |
|
|
|
|
|
|
|
|
|
|
Découverte .Sur Les SUITES ou PROGRESSIONS GEOMETRIQUES. |
|
|
|
|
Exemple : La population d’une grande ville
française est de un million d’habitants (on se considère en l’
année 1) .Elle augmente de 1 % par an. Questions : · Quelle
est l’augmentation de la population en l’année « 2 » ? · Quelle
est la population totale à la fin de l’année 2 ? · Par
combien faut-il multiplier la population de l’année 1 pour avoir la
population de l’année 2 ? |
|
|
|
Première étape : |
Deuxième
étape |
Troisième
étape : |
|
|
|
U 2
= la somme de 100% de la population
plus 1% de la population |
On factorise : |
On remplace la
donnée statistique « 100
% » par la fraction : |
Et « 1% » par la fraction : |
|
Population en l’année 2 ( U 2 ) |
U 2
= 100 % de 1 000 000 + 1% de 1 000 000 |
U 2
= 1 000 000 ( 100 % + 1 % ) |
|
|
|
|
|
U 2
= 1 000 000 ( |
On calcule : que l’on remplace par la valeur
décimale : 1,01 |
|
En
conclusion : U 2 = 100 %
de 1 000 000 + 1% de 1 000 000 devient le calcul :
1 000 000 h x 1,01 =
1 010 000 habitants
Vérification : Ce qui correspond bien à la somme
de : 1000 000 h plus
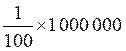 h
soit 1 000 000 h + 10 000 h = 1 010 000 h
h
soit 1 000 000 h + 10 000 h = 1 010 000 h
On se propose de
compléter le tableau suivant :
|
|
|
Population |
|
|
|
Population en
l’année 1 ( U 1 ) |
U 1 = 1
fois 1 000 000 ou 100 % de
1 000 000 |
|
|
|
|
Population en
l’année 2 ( U 2 ) |
U 2
= 100 % de 1 000 000 + 1% de 1 000 000 |
U 2
= 1 000 000 ( 100 % + 1 % ) |
1 000 000
h x 1,01 = 1 010 000 habitants |
|
|
Population en
l’année 3 ( U 3 ) |
U 3 =
1 010 000 + 1% de 1 010 000 |
U 2
= |
|
|
|
Population en
l’année 4 ( U 4 ) |
|
|
|
|
|
Population en
l’année 5 ( U 5 ) |
|
|
|
|
|
Population en
l’année 6 ( U 6 ) |
|
|
|
|
|
|
|
|
|
|
|
Population en
l’année « n » ( U n ) |
|
|
|
|
Calcul de U 3 = 1 010 000 + 0,01 de 1 010 000 :
1 000 000 h ![]() x 1,01 x 0, 01 =
x 1,01 x 0, 01 =