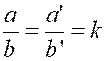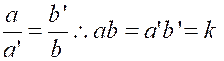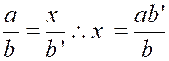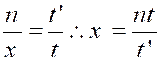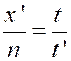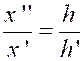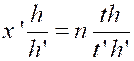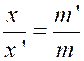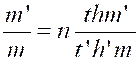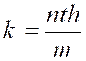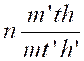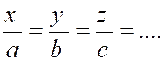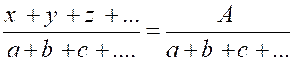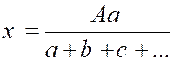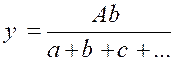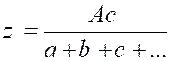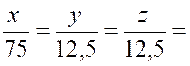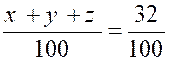Info +notion++

LES GRANDEURS PROPORTIONNELLES.

Info ++

Deux grandeurs « A » et « B » sont « directement proportionnelles » , ou simplement « proportionnelles » , ou « en raison directe » l’une de l’autre, lorsque deux valeurs quelconques de l’une sont dans le même rapport que les deux valeurs correspondantes de l’autre.

Deux grandeurs « A » et « B » sont « inversement proportionnelles » , ou « en raison inverse » l’une de l’autre, lorsque deux valeurs quelconques de l’une sont dans le même rapport inverse  que les deux valeurs correspondantes de l’autre.

Exemples :

Série N°1 : sur des situations proportionnelles.

·       Le salaire d’un ouvrier est généralement , par convention, proportionnel au nombre de ses journées de travail.

·       La quantité de vivres nécessaire à l’approvisionnement d’un navire est évidemment en proportion avec la durée du voyage à entreprendre.

·       En physique , on établit que la masse d’un corps homogène est en raison direct  de son volume.

·       En géométrie : on démontre que la circonférence , l’air et le volume d’une sphère sont respectivement proportionnels à la longueur du rayon de la sphère, au carré de cette longueur et au cube de cette longueur.

Série 2 : sur des situations inversement proportionnelles.

·       Le temps nécessaire à une escouade  d’ouvrier pour couler une dalle de béton est , en général, inversement proportionnel au nombre d’ouvriers employés.

·       En physique , on établit que le volume d’un corps est en raison inverse de sa densité.

·       En physique encore , on démontre que l’intensité de la lumière reçue par une surface donnée est en raison inverse du carré de la distance entre cette surface et la source de la lumière : à «  2 ; 3 ; 4 ;…n » mètres de cette source , la surface est «  4 ; 9 ; 16 ; …..n² » fois moins éclairée qu’à un mètre.

·       En algèbre et en arithmétique , on n’a pas à démontrer la proportionnalité , directe ou indirecte , des grandeurs considérées dans une question : cette proportionnalité est un fait acquis à l’avance , soit qu’elle résulte d’une convention, soit qu’elle s’impose évidemment par la force même des choses, soit qu’elle ait été établie ailleurs par une démonstration spéciale.

Autre cas : Une grandeur peut être , à la fois , proportionnelles directement à certaines grandeurs et proportionnelle inversement à certaines autres.

Exemple : Le temps nécessaire pour le creusement d’une tranchée est , à la fois , en raison directe de la longueur de la tranchée et en raison inverse du nombre d’ouvriers employés.

Les proportions.

On établit en arithmétique ces deux principes :

·       Pour que deux grandeurs soient proportionnelles l’une à l’autre, il faut et il suffit qu’elles varient dans le même rapport ; c'est-à-dire que si l’une devient « n » fois plus grande qu’elle n’était, l’autre devienne aussi « n » fois plus grande.

·       Pour que deux grandeurs soient inversement proportionnelles l’une à l’autre, il faut et il suffit qu’elles varient dans le rapport inverse ; c'est-à-dire que si l’une devient « n » fois plus grande qu’elle n’était, l’autre devienne aussi « n » fois plus petite qu’elle n’était.

·       On prouve aussi, en arithmétique que si « deux grandeurs sont proportionnelles », le rapport de leurs valeurs correspondantes est constante :

Et que si « deux grandeurs sont inversement proportionnes », le produit de leurs valeurs correspondantes est constante :

Il est utile de remarquer que cette constante est , dans l’un et l’autre cas , la valeur numérique de « a » lorsque « b » devient égal à l’unité.

Info +++

Règle de trois.

La règle de trois simple  a pour objet de fournir le terme inconnu d’une proportion dont les autres termes sont donnés. Elle s’applique aux questions dont voici l’énoncé général est :

« Connaissant deux valeurs « a » et « b » de deux grandeurs directement ou inversement proportionnelles « A » et « B » , trouver la valeur « x » de la première grandeur « A » qui correspond à une nouvelle valeur « b’ » attribuée à l’autre grandeur « B ».

Exemples :

N°1 : On achète pour « a » euros « b » mètres d’étoffe, combien coûteront « b’ » mètres ?

Admettant la proportionnalité entre le prix  et la longueur , on a :

N°2 : Il a fallu « n » ouvriers pour exécuter en « t » jours un certain ouvrage , combien d’ouvriers  eût-il fallu pour exécuter en « t’ » jours ?.

Si l’on admet que le nombre des ouvriers et le nombre des journées varie en raison inverse , on a :

La  «  règle de trois composée »  a pour objet  le calcul d’une quantité qui entre comme terme inconnu dans plusieurs proportions à trois termes connus. Cette règle sert à résoudre des problèmes du type général suivant :

Exemple :

Il a fallut « t » jours à « n » ouvriers, travaillant « h » heures par jour, pour exécuter un terrassement de «  m » mètres cubes ; combien d’ouvriers faudra-t-il pour exécuter en « t’ » journées de « h’ » heures un terrassement de « m’ » mètres cubes ?

Formons le tableau des éléments de la question :

« t » jours

« n » ouvriers

« h » heures

«  m » mètres

« t’» jours

« x » ouvriers

« h’ » heures

« m’ » mètres

Ramenons la question à une suite de règles de trois simples.

Soit « x’ » le nombre d’ouvriers nécessaire pour exécuter en « t’ » jours l’ouvrage primitif, la journée de travail restant de « h » heures ; on a   d’où « x’ = n ».

Soit « x’’ » le nombre d’ouvriers nécessaire pour exécuter en « t’ » jours l’ouvrage primitif , à raison de « h’ » heures de travail par jour ; on a «   » ; d’où « x’’=   »

Soit « x » le nombre d’ouvriers nécessaire pour exécuter en « t’ » journées de « h’ » heures le nouvelle ouvrage de « m’ » mètres cubes , on a «  » , d’où  « x =  » .

On voit que , dans la règle de trois composée, l’inconnue est égale au produit de la valeur primitive de même espèce qu’elle, par les rapports, les uns directs , les autres inverses, entre les valeurs nouvelles et les valeurs primitives des autres grandeurs , -rapports directs , si ces grandeurs sont directement proportionnelles à l’inconnue, rapports inverses, si ces grandeurs lui sont inversement proportionnelles.

Info ++

Réduction à l’ UNITE.

Les questions qui se ramènent aux règles de trois peuvent se traiter par la « réduction » à l’unité. Dans cette méthode , on calcule préalablement la valeur de la grandeur de même espèce que l’inconnue qui correspond à l’hypothèse où toutes les autres grandeurs deviennent égales à l’unité ; en d’autres termes, on détermine la « constante (k)  » qui permet d’établir une relation générale entre les grandeurs considérées.

Exemples :

N°1 : On achète pour « a » euros « b » mètres d’étoffe, combien coûteront « b’ » mètres ?

« b » mètres coûtent « a » euros ;

« 1 » mètre coûte «  » euros ;

« b’ » mètres coûtent « b’ x  » euros  , d’où  « x =  »

N°2 :Il a fallut « t » jours à « n » ouvriers, travaillant « h » heures par jour, pour exécuter un ouvrage  de «  m » mètres cubes ; combien d’ouvriers faudra-t-il pour exécuter en « t’ » journées de « h’ » heures un terrassement de « m’ » mètres cubes ?

« n » ouvriers en « t » journées de « h » heures font « m » mètres cubes.

« n t » ouvriers en « 1  » journées de « h » heures font « m » mètres cubes.

« n t h » ouvriers en « 1  » journées de « 1 » heures font « m » mètres cubes.

«  » ouvriers en « 1  » journées de « 1 » heures font « 1 » mètre  cube.

On obtiendra « x » en multipliant par « m’ » et en divisant par « t’ » et par « h’ » la constante «  » ; il viendra «  x =

Info ++++

Partages proportionnels.

++Info =

Partager une quantité « A » en parties «  x ; y ;z ;.. »proportionnelles à des quantités données «  a ; b ; c ; .. » c’est la partager en parties telles que les rapports respectifs entre ces parties et ces quantités données soient égaux, c’est – à – dire en sorte que l’on ait :

«  x + y + z + ..= A  »   ;  «  »

En vertu des propriétés des suites de rapports égaux  (info +++)   on a :

«  »  =   «  » ;

d’ où :   ;  ;

Exemple : Trouver la composition de 32 kg de poudre de guerre , sachant que la poudre est un mélange de 75 parties , sur 100, de salpêtre ou azotate de potasse ,, de 12,5 partie de soufre et de 12,5 partie de charbon .

Solution :  ;   donc : x= 24 ; y = 4 ; z = 4

Remarquons qu’en vertu de ces formules on peut , sans altérer les résultats , multiplier ou diviser à l’avance par une même quantité les quantités données « a ; b ; c »  

Refaire les exercices du cours……