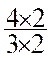Pré requis:

Lecture : Transformation d’une fraction

Fraction : nomenclature

Géométrie : les opérations sur un ou des segments en général , et en particulier : la fraction d’un segment.

ENVIRONNEMENT du dossier:

Index warmaths.fr

AVANT : nomenclature

COURS

APRES : Transformation d’une fraction 2°) Fractions algébriques

Complément d’Informations sur la fraction

TITRE : Propriétés des fractions

Travaux ; devoirs				Corrigé
TEST	Contrôle	évaluation	Fiches d’activités en arithmétique	Contrôle	évaluation

COURS

Les propriétés des fractions :

A) Multiplication du numérateur par un nombre : INFO +++

Soit la fraction , si je multiplie le numérateur par 4 , on obtient .

La fraction a été multipliée par 4 ; en effet : les parties de l’unité n’ont pas changé de valeur , mais nous en avons 4 fois plus ; on énonce :

« Lorsqu’on multiplie une fraction par un nombre on multiplie le numérateur de la fraction par un nombre .On dit que « la fraction est multipliée par ce nombre ».

B) Division du numérateur par un nombre . INFO+++

Dans l’exemple précédent , si je divise le numérateur par 4 ,j’obtient . La fraction est divisée par 4 , en effet , les parties n’ont pas changé , ce sont toujours des « tiers » , mais nous en avons 4 fois moins .

Donc «  lorsque l’on divise une fraction par un nombre on divise le numérateur de la fraction par ce nombre ».

C) Multiplication du dénominateur : INFO ++++

Prenons la fraction , si je multiplie le dénominateur par 4 j’obtient et la fraction est divisée par 4 . Dans les deux cas le nombre des parties , quatre , est la même , mais dans le second , ce sont des douzièmes , quatre fois plus petits , par conséquent :

lorsque l’on multiplie le dénominateur d’une fraction par un nombre , la fraction est divisée par ce nombre .

D) division du dénominateur : INFO +++

Si je divise le dénominateur de par 4 , j’obtient , mais comme les tiers sont quatre fois plus grands que les douzièmes , la fraction a été multipliée par 4 ; donc : Lorsqu’on divise le dénominateur d’une fraction par un nombre , la fraction est multipliée par ce nombre .

E ) Multiplication et division des deux termes par un même nombre .

Si l’on multiplie les deux termes 4 et 3 de par un même nombre , 2 par exemple  , nous obtenons = . Nous avons deux fois plus de parties , ( 8 au lieu de 4) , mais ces parties sont deux fois plus petite , donc la fraction n’a pas changée de valeur .

Si je divise au contraire les deux termes de par deux , j’obtient =j’ai deux fois moins de parties , mais ces parties sont deux fois plus grandes . Donc « lorsqu’on multiplie ou qu’on divise les deux termes d’une fraction par un même nombre , la fraction ne change pas de valeur ».

F ) Conséquences :

1°) On rend une fraction 2 ;3 ;4 ;.. fois plus grande , soit en multipliant son numérateur par 2 ;3 ;4 ;.., ce qui est toujours possible ; soit en divisant son dénominateur par 2 ;3 ;4 ;…, lorsque l’opération peut s ‘effectuer.

2°) On rend une fraction 2 ;3 ;4 ;.. fois plus petite , soit en multipliant son dénominateur par 2 ;3 ;4 ;.., ce qui est toujours possible ; soit en divisant son numérateur par 2 ;3 ;4 ;…, lorsque l’opération peut s ‘effectuer.

3°) On peut simplifier les termes d’une fraction en divisant le numérateur et le dénominateur par un même nombre . INFO ++++

4°) On peut réduire les fractions à un même dénominateur en multipliant les deux termes de chacune par un nombre déterminé, (ce nombre étant le dénominateur de l’autre ou des autres ) INFO ++++

INFORMATIONS COMPLEMENTAIRES :

Liste à consulter sur	INFO plus ++++
1. Simplification de fractions
2. Réduction des fractions au même dénominateur.
3. Opérations sur les fractions :Addition ; Soustraction ; Multiplication ; Division
4. Fractions décimales
5. Fraction d’un nombre
6. Fraction de fraction
7. Inverse d’une fraction
8. Activités problèmes
9. Problèmes amusants

TRAVAUX AUTO FORMATIFS.

CONTROLE:

Compléter les phrases suivantes :

D) Multiplication du numérateur par un nombre : INFO +++

« Lorsqu’on multiplie une fraction par un nombre ……………

E) Division du numérateur par un nombre . INFO+++

Lorsque l’on divise une fraction par un nombre on divise …………………..

F) Multiplication du dénominateur : INFO ++++

lorsque l’on multiplie le dénominateur d’une fraction par un nombre , …………………..

G ) division du dénominateur : INFO +++

: Lorsqu’on divise le dénominateur d’une fraction par un nombre , …………………..

H ) Multiplication et division des deux termes par un même nombre .

Lorsqu’on multiplie ou qu’on divise les deux termes d’une fraction par un même nombre , …………………………….. .

K ) Conséquences :

1°) On rend une fraction 2 ;3 ;4 ;.. fois plus grande , soit ……………………..

2°) On rend une fraction 2 ;3 ;4 ;.. fois plus petite , ……………………………

3°) On peut simplifier les termes d’une fraction en ……………………………

4°) On peut réduire les fractions à un même dénominateur en ……………………

EVALUATION:

Pour chaque cas donner un exemple numérique.