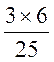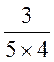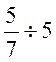DOSSIER : FRACTION d’un SEGMENT de DROITE

I ) Fraction d’une longueur

II )  FRACTION de l’ UNITE

III  )   Lecture d’une fraction

I V )  Comparaison des fractions  avec l’unité

V  ) FRACTIONS DECIMALES

PROPRIETES FONDEMMENTALES DES FRACTIONS CONSEQUENCES :

VI )  Fractions « égales »

V II ) SIMPLIFICATION de FRACTIONS

V III  ) REDUCTION DES FRACTIONS AU MEME DENOMINATEUR :

IX  )  COMPARAISON DES FRACTIONS ENTRES ELLES.

X )  OPERATIONS SUR LES FRACTIONS : ( addition ; soustraction ; multiplication ;division)

COURS

I ) Fraction d’une longueur

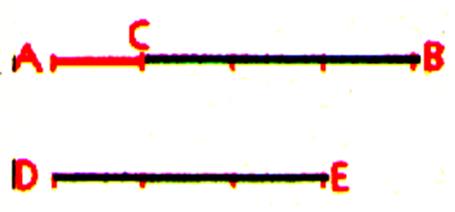
Exercice : soit un segment de droite AB ;

A ) Nous partageons ce segment  de droite quatre parties égales  ou encore nous divisons la longueur  de ce segment par 4 ; chacune des parties obtenues est dite le quart de la longueur AB , on écrit :

AC =de AB

B ) Faisons la somme de trois de ces parties ce qui revient à multiplier par 3 l’une de ces parties : la longueur du segment DE ainsi obtenue est les trois quarts de la longueur AB :

DE = de AB .

Nous avons fait deux opérations :

1°)nous avons divisé une longueur AB par un nombre entier « 4 » .

2°)Nous avons multiplié l’une des parts ainsi obtenues par un nombre entier « 3 ».

cette double opération se traduit par la notation : de AB  ou

elle indique que l’on a pris une fraction d’un segment de droite AB.

Dans la fraction  :

« 4 » est appelé  « le dénominateur » de la fraction : il indique en combien de fois de parties égales la longueur AB a été divisée.

« 3 »  est appelé « le numérateur » de la fraction : il indique par quel nombre entier on a multiplié l’une des parts ainsi obtenues.

« 4 » et « 3 » sont encore les deux termes de la fraction.

II )  FRACTION de l’ UNITE

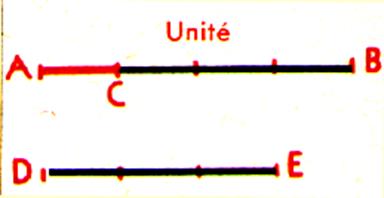
Dans l’exercice  précédent  nous avons  supposé que AB était une longueur quelconque , mais si AB est l’unité de longueur « 1 »,  est alors une fraction de l’unité   .

On écrit alors que DE =   ( sous entendu de l’unité « 1 »)

 représente la mesure de DE  si nous prenons AB comme unité .

 est un nombre qui porte le nom de « nombre fractionnaire » , ou fraction.

III  )   Lecture d’une fraction

Voir : « fraction nomenclature »

I V )  Comparaison des fractions  avec l’unité

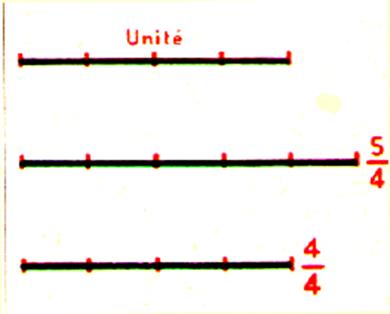
Dans l’exercice précédent la longueur DE étant plus petite  que l’unité la fraction  est elle même plus petite que l’unité .

On remarque que le numérateur est plus petit que le dénominateur.

Si au lieu de prendre  de l’unité  nous en prenons les  il est évident que le segment obtenu est plus grand que l’unité et  la fraction  est elle même plus grande que l’unité : son numérateur est plus grand que son dénominateur .

Enfin l’unité peut être  représentée par la fraction  ; le numérateur et le dénominateur sont égaux.

En résumé :

Numérateur < dénominateur            ®                  fraction < unité

Numérateur > dénominateur            ®                fraction > unité

Numérateur  = dénominateur               ®                  fraction  = unité

V  ) FRACTIONS DECIMALES

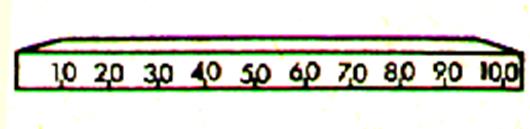
Si nous prenons un mètre rigide en divisé en dix parties égales , chacune de ces parties  ou décimètre représente le dixième de mètre et sept  de ces parties , (par exemple) , représentent les sept dixièmes du mètre ; le nombre qui représente ces sept dixièmes  de longueur s’écrit :  

Si chaque décimètre est à son tour divisé en dix parties égales , chacune de ces nouvelles parties  ou centimètre représente un centième de mètre  et trois de ces parties représentent les trois centièmes de mètre , le nombre correspondant s’écrit :

 Remarque :  ;  sont des fractions décimales .

Nous avons donc deux sortes de  fractions :

Si  le dénominateur est égal à 10 ; 100 ; 1000  , la fraction est décimale …….Pour en savoir plus ! ! !

si le dénominateur est un nombre entier quelconque (autre que 2 ; 5 ou un multiple de 2 et ou 5 )la fraction est dite «ordinaire » 

PROPRIETES FONDEMMENTALES DES FRACTIONS CONSEQUENCES

VI )  Fractions « égales »

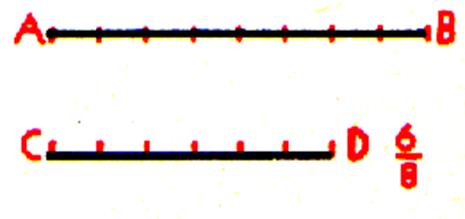
Pour prendre les d’un segment AB , il faut d’abord diviser ce segment en 8 parties égales , puis prendre 6 de ces parties.

CD =  de AB

Si au lieu de diviser en 8 parties , nous le partageons en 16 parties égales , la même longueur CD contiendra  12 de ces parties au lieu de 6 , il est évident que les fractions   et  sont égales , puisqu’elles mesurent  une même longueur , nous pouvons écrire :

 =  =

une fraction ne change pas de valeur si l’on multiplie ses deux termes par un même nombre.

Voir « fractions équivalentes »

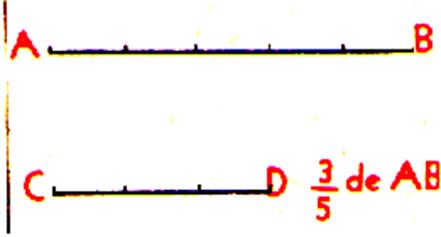
Si maintenant nous partageons AB en 4 parties égales , la même longueur  CD contiendra 3 de ces parties :

CD =   de AB

Il est bien évident encore que :

 =  =

NOTA : une fraction ne change pas de valeur , si l’on divise ses deux termes par un  même nombre.

V II ) SIMPLIFICATION de FRACTIONS

Pour en savoir plus ! ! !

Simplifier une fraction , c’est obtenir une fraction égale à la fraction donnée mais dont les deux termes sont plus petits que ceux de  cette fraction.

Lorsque nous écrivons  =  nous avons simplifié la fraction.

Règle : pour simplifier une fraction , on divise ses deux termes par un même nombre.

Remarque : si les deux termes de la fraction ne peuvent être divisés par un même nombre , on dit que la fraction est « irréductible » ;  est irréductible.

V III  ) REDUCTION DES FRACTIONS AU MEME DENOMINATEUR :

Pour en savoir plus ! !

Soient les deux fractions  et , on peut écrire :

 =  =       ;  ==

on dit que les deux fractions  et  sont réduite au même dénominateur.

Règle : pour réduire deux fractions au même dénominateur    on multiplie les deux termes de chacune d’elles par le dénominateur de l’autre .

Remarques : dans l’exemple précédent  , on a pris comme dénominateur commun le produit des dénominateurs ; dans certains cas , on a intérêt à prendre comme dénominateur commun un dénominateur plus petit.

Exemple : soit à réduire au même dénominateur , les fractions     et   au lieu de prendre comme dénominateur  commun 8  6 = 48 , il est plus simple de prendre comme dénominateur  commun « 24 ».

  =    et      =

IX  )  COMPARAISON DES FRACTIONS ENTRES ELLES.

Pour en savoir plus ! !

Premier cas :

Les deux fractions ont le même dénominateur :

Soit à comparer  et   un schéma nous permet d’écrire que   < 

En résumé : si deux fractions ont le même dénominateur  , la plus grande est celle qui a le plus grand numérateur.

Deuxième cas :

les deux fractions ont le même numérateur :

Soit à comparer  et  , un schéma nous permet d’écrire :  <   

En résumé : si deux fractions ont le même numérateur   , la plus grande est celle qui a le plus petit dénominateur .

Troisième cas :

Les deux fractions n’ont ni le même dénominateur ni le même numérateur : on commence  par les réduire au même dénominateur , puis on compare entre elles les fractions ainsi obtenues .

Exemple soit à comparer :  et

On réduit les deux fractions au même dénominateur.

 =  =    ; et   = =

or   <   donc   <

X )  OPERATIONS SUR LES FRACTIONS

ADDITION de  fractions :

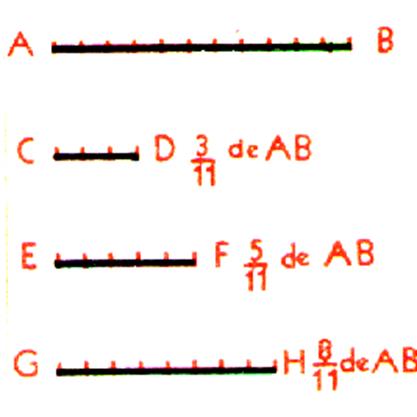
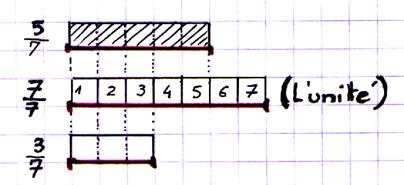
Soit un segment de droite AB et deux segment CD et EF tels que :

CD = 3 onzièmes de AB  =  de AB

EF = 5 onzièmes de AB  =  de AB

Si nous faisons la somme de ces deux segments , nous trouvons :

GH = 8 onzièmes de AB =  de AB

Nous pouvons écrire :

3 onzièmes de AB + 5 onzièmes de AB = 8 onzièmes de AB .

 de AB + de AB  =  de AB

Pour en savoir plus ! ! ! ! !

La somme de deux fractions qui ont le même dénominateur est une fraction qui a pour dénominateur  le dénominateur commun  aux deux fractions et pour numérateur la somme  de leurs numérateurs.

Remarque : si deux  fractions sont quelconques , on les simplifie. S’il y a lieu , puis on les réduit au même dénominateur.

Pour en savoir plus ! ! ! !

Exemple :

+= ?    devient  après simplification += ?

réduction au même dénominateur :

+=  devient   +

opération : + =

SOUSTRACTION de deux fractions :

Un segment mesure  de mètre ; vous en effacez les de mètre  .Quelle est la longueur restante ?

pour en savoir plus ! ! ! ! !

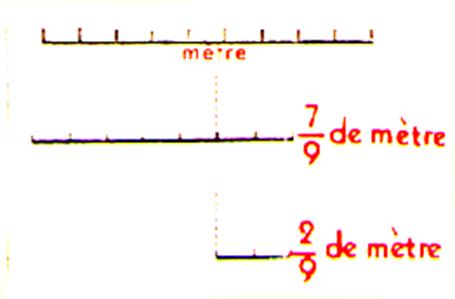
Nous représentons graphiquement les longueurs données. Le graphique nous montre immédiatement que la longueur restante est  de mètre :

7 neuvièmes de mètre – 5 neuvièmes de mètre  = 2 neuvièmes de mètre 

on peut écrire :

 de mètre - de mètre =  de mètre 

ou encore :

 - =

La différence de deux fractions qui ont le même dénominateur est une fraction qui a pour  dénominateur le dénominateur commun  et pour  numérateur  la différence des deux numérateurs.

CAS: lorsque les deux fractions sont quelconques on les simplifie , s’il y a lieu , puis on les réduit au même dénominateur.

Exemple :

Effectuer - = ?

On simplifie : - = ?

On réduit au même dénominateur :

- = ?  devient - = ?

calcul : - = 

Pour en savoir plus ! !

Multiplication de deux fractions

Pour en savoir plus ! ! !

Multiplication par un nombre entier :

Un brodeur a exécuté en une journée les   d’un tapis. Quelle fraction de la longueur totale exécute – t – il  en 6 jours ?

La fraction cherchée est  6

Ou

+++++=  ;

soit du tapis .

Le produit d’une fraction par un nombre entier est une fraction qui a pour numérateur le produit du numérateur de la fraction par le nombre entier et pour dénominateur le dénominateur de la fraction donnée.

Pour en savoir plus ! ! ! !

DIVISION par un nombre entier

Pour en savoir plus ! ! !

Soit diviser par 4 les  d’un segment donné :

Nous représentons les du segment AB , soit CD le segment obtenu , il s’agit de partager CD en quatre parties égales.

           Si au lieu de partager AB en cinq parties égales , nous l’avions partagé en  5  4 =20 parties égales  , il est évident  que le segment EF  qui contient 3 de ces parties  est 4 fois plus petit que le segment CD , or

EF = de AB .

Donc :  : 4 =  =

Le quotient d’une fraction par un nombre entier est une fraction qui a pour numérateur , le numérateur de la fraction donnée et pour dénominateur le produit du dénominateur de cette fraction par le nombre entier.

Remarque générale  :  sauf quelques cas particuliers , on a toujours intérêt , lorsque cela est possible , à simplifier les fractions avant même d’effectuer les opérations sur ces fractions.

TRAVAUX AUTO – FORMATIFS.

CONTROLE:

Voir cas par cas ; aller  aux dossiers   « pour en savoir plus ! ! !» 

EVALUATION:

Exercices :

N°1

N°2

N°3

N°4

N°5

PROBLEMES

N°1

N°2

N°3

N°5

J’ai acheté Les  d’un mètre de tissu ; j’ai dépensé 240 Euros , calculer le prix du mètre de ce tissu.

N°6

Pour faire un gâteau au chocolat une cuisinière a utilisé 150 grammes de chocolat  , à 72 F. le kilo ; du beurre à 60 F. le kilo et du sucre en poudre à 10,40 F. le kilo. Calculer le prix de revient du gâteau sachant que le poids du beurre  est le tiers du poids de chocolat et le poids du sucre les  5 /6  du poids chocolat.

Il faut en outre 3 œufs à 12 F la douzaine    et 75 grammes de farine a 8 F le kilo . Avec ce gâteau on peut servir 8 personnes , calculer le prix de revient d’une part.

N°7

Pour faire du savon on utilise la formule suivante :

  On obtient à l’aide de ces proportions 12 morceaux de savon.

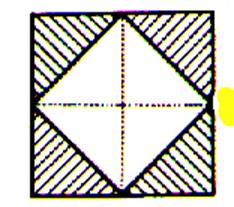
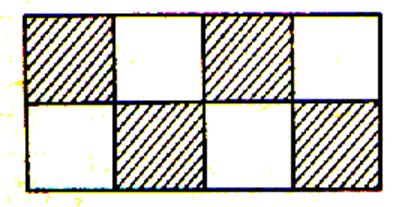
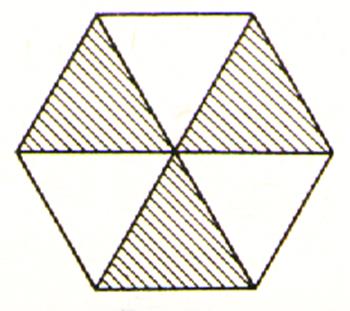
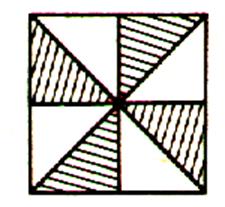
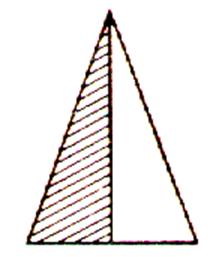
Quel est le poids de l’un d’eux sachant qu’à la cuisson le mélange perd 1/5 de son poids ?

N°8

Dans chacune des figures suivantes  , dites quelle fraction de la surface totale représente chacune des parties hachurées ?

N°9

La préparation d’un plat demande deux heures . On compte 1 /8 du temps total pour l’épluchage des légumes , ¼ du temps total pour la cuisson à feu vif  et le reste du temps pur la cuisson à feu doux.

Quelle fraction du temps total représente la cuisson à feu doux ? évaluer ce temps en minutes .

N°10

Une somme  de 20850 F a été partagée entre trois personnes . La première a eu 11 250 F et la part de la deuxième vaut  le 1/3 de la part de la troisième .Calculer les deux dernières parts.

N°11

Un bénéfice est égal au 12 /25  du prix d’achat. Quelle fraction du prix d’achat  représente le prix de vente ? Quel est le prix de vente si le prix d’achat est égal à 5 000F ?

Un segment de droite mesure 270 mm. Partagez – le en trois  parties  de manière que le deuxième segment soit les 2/3 du premier et que le troisième soit égal à la demi- somme  des deux  premiers segments
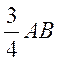
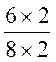
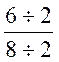
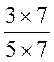
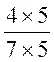
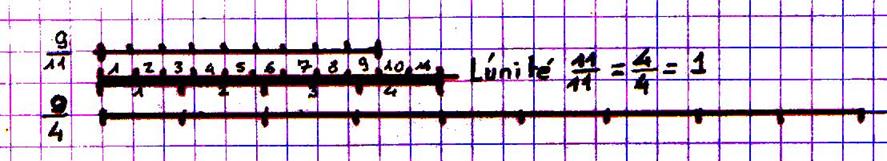
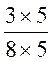
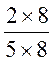