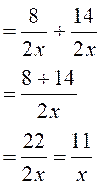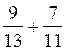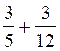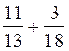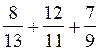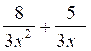Définition de l’objectif :       Addition de deux fractions ayant des dénominateurs différents :    exemple    ()

   L’addition deux fractions n’ayant pas le même dénominateur ne se fait pas ; il faut transformer  chaque fraction en fraction équivalente ,mais en prenant soin de  donner à chaque nouvelle fraction  le même dénominateur ,de telle sorte qu’elles aient « un dénominateur commun , on dit communément aussi « réduire au même dénominateur».

Modèle mathématique: =    ne se fait pas

Remarques:

  En calcul numérique on peut se satisfaire de la solution suivante (mais à condition de savoir rendre irréductible une fraction: (Cette méthode ne pourra pas être applicable au calcul algébrique)

        Pour pouvoir obtenir un résultat on transforme les fraction en fractions équivalentes dont on donnera un dénominateur égal au produit des dénominateurs.

Ici le dénominateur commun sera  «  bd »

on transforme  la première fraction :

on transforme la deuxième fraction :

On transforme l’égalité de départ:* :                =

On peut maintenant effectuer l addition des deux fractions:     =

Procédure permettant de  contourner le problème de ne pouvoir additionner (ou soustraire) des fractions de dénominateur différent:

(Ce travail se fait en 6 étapes )

a)  Rendre irréductible les fractions.

b) Calculer le plus petit dénominateur commun.(PPDC des dénominateurs)  ( dit aussi « ppcm »)

c) Transformer chaque fraction rendue irréductible en fraction équivalente (de dénominateur égal au PPDC calculer précédemment)

                * faire la vérification .

d) Rendre compte

              poser l’égalité  dont le premier membre est l’addition de départ et le second membre est la nouvelle addition.

e) Faire l’addition des nouvelles fractions: (voir procédure concernant l’addition de fractions de même dénominateur.)

f)  Rendre compte sous forme d’égalité:

                l’addition de départ égale au résultat obtenu précédemment.

Exemple d’application:

EXERCICE résolu  :   Calculer    

1°)  rendre  irréductible les deux fractions.

2°)  Calculer le Plus Petit Dénominateur Commun :des deux dénominateurs (7  et 11 ).

             Le PPCM de ( 7 ; 11 ) est   égal à   7 fois11  =   77

3°) .

a) Transformation de la première fraction en fraction équivalente de dénominateur  égal à 77  :

Calcul du « k » =  77 : 7  ;  « k » =11 

Ce qui donne              ( fraction équivalente à  3 / 7 )

b) Transformation de la deuxième fraction en fraction équivalente de dénominateur égal à 77

On calcule « k »=  77 : 11 =  7  (on doit donc multiplier le numérateur par 7)

Ce qui donne:

              4° )  Rendre compte sous forme d’une égalité:

                5 °) Calcul de l’addition:

==

               6°) Conclusion:

= 

ALGEBRE:

TRAVAUX AUTO FORMATIFS.

CONTROLE:

1°)  Dans quel cas est - il impossible d’effectuer l’addition de deux fractions?

2°)   Combien y a-t-il d’étapes à franchir pour pouvoir transformer deux fractions de dénominateur différent en vu de faire une addition (ou une soustraction) de ces deux fractions transformées en fraction équivalente de même dénominateur.

3°)   Citer les 6 étapes (dans l’ordre chronologique ) permettant de pouvoir parvenir à un résultat concernant l’addition de deux fractions de dénominateur différent.

EVALUATION:

1°)Faire les additions suivantes :

a) =                b )  =               c )  = ;

2 °)     idem

a ) =

3°) mettre au même dénominateur :

 =

3°) Idem

a)  =    

b)    b)      =
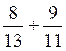
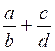
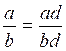
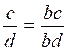
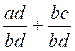
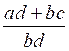
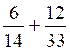
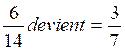
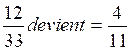
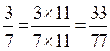
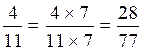
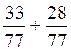
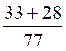
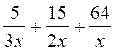
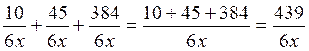
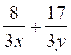
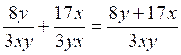
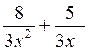
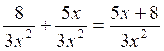
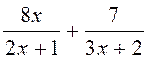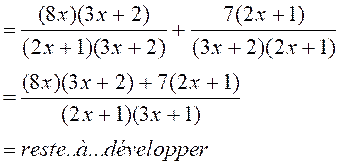
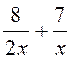