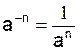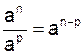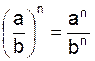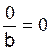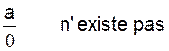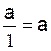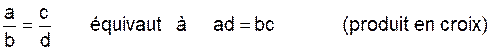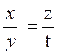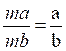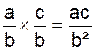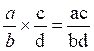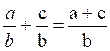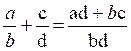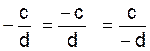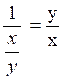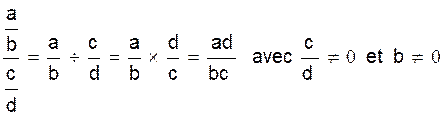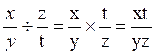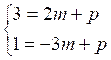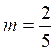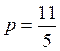Classes : BEP / SECONDE. / niveau IV

Pré requis:

L’ensemble des Réels

Arithmétique : les 4 opérations (révisions)

Les opérations avec les décimaux relatifs : Addition - Soustraction – Multiplication – Divisions – Rationnels

ENVIRONNEMENT du dossier:

Index

AVANT : Les D relatifs

COURS

APRES : 1°) Les égalités et …… 2°) suite sur les relation d’ordre, intervalles,…. 3°) Préparation concours.

Complément d’Info : Le calcul numérique. Programme de la classe de seconde.

TITRE : RESUME 1 : TRAVAUX NUMERIQUES (niveau 4 : 3^è/seconde).

I) Les ensembles

II) Opérations

III) Les règles de calculs.

IV ) Puissance d’un réel « a » non nul

V) Notations "scientifique" et "ingénieur" .

VI) Opérations sur les quotients.

VII) Opérations sur les radicaux .

Les opérations avec les nombres Réels.

Travaux ; devoirs			Corrigé
TEST	Contrôle	évaluation	Contrôle	évaluation

Ici : ► Liste des pré requis : travaux et cours joints : Interdisciplinarités : (matière concernée)

COURS

Un nombre peut - être désigné de diverses façons. Lorsqu'on cherche une manière simple de désigner un nombre défini par une certaine écriture, c'est en fait cette écriture que l'on simplifie, et non le nombre donné sans ambiguïté par l'énoncé. Lorsqu'une écriture contient des lettres, et désigne un nombre, chaque fois que les lettres sont remplacées des nombres, on appelle cette écriture "expression algébrique" . Ex: 2x+5y- z

Info +

I ) Rappels : LES ENSEMBLES

Info +

( Info basiques sur les ensembles )

On retiendra que :

N désigne l’ensemble des nombres entiers naturels.

Z désigne l’ensemble des nombres entiers relatifs

D désigne l’ensemble des nombres décimaux

Q désigne l’ensemble des nombres rationnels.

R désigne l’ensemble des nombres réels. ( les réels non rationnels sont dit irrationnels.

En résumé : N Ì Z Ì D Ì Q Ì R

Info

II ) OPERATIONS

Info +

L’addition vérifie les propriétés suivantes :

Quels que soient les réels « a », « b », et « c »

	A vérifier avec des nombres.
a + b = b +a
a + ( b + c ) = ( a + b ) +c
a + 0 = a

Il existe un seul réel qui , ajouté à “a” donne « 0 » : c’est l’opposé de « a », que l’on note « -a »

( on n’a plus de soustraction : on ajoute au premier l’opposé du second)

La multiplication vérifie les propriétés suivantes :

Quels que soient les réels « a », « b », et « c »

	A vérifier avec des nombres.
a b = b a
a ( b c) = ( ab )c
a ´ 1 = a

Si « a » est différent de « 0 », il existe un seul réel qui , multiplié par « a », donne « 1 » : c’est l’inverse de « a » que l’on note :

Remarques :

►le réel « 0 » n’ a pas d’inverse. ( ce qui fait dire que l’on ne peut pas diviser par « 0 »)

►On n’a plus de division : on multiplie le « numérateur » ou « dividende » par l’inverse du « dénominateur » ou « diviseur ».

La multiplication est distributive par rapport à l’addition c’est à dire que :

Quels que soient les réels « a », « b », et « c » on a «  a ( b + c ) = a b + ac »

Info ----

III ) REGLES DE CALCUL

Info ++++

►Soit « a » , « b » , « c », et « d » et « x » des réels.

Par définition, on pose :

a - b = a + ( -b)

et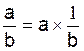

► Un produit de deux nombres est nul si , et seulement si, l'un au moins des deux nombres est nul.

Si ab = 0 alors obligatoirement , a = 0 ou b = 0 .

Si a ¹ 0 , alors a x = b équivaut à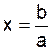

►Quels que soient les nombres "a" et"b" :

	À vérifier avec des nombres
- ( -a) = a
a (-b) = - (a b) = (-a)b ; (-a)(-b) = a b
( - a ) b = a ( - b ) = - a b
-(a + b) = (-a) + (-b) = (par simplification) = -a -b
- ( a - b ) = -a + b
a + x = b équivaut x = b - a

►voir ci dessous les «  Identités Remarquables » . 

Info

IV ) PUISSANCE D’un réel « a » non nul

Info +

Quel que soit le nombre non nul a, et quel que soit l'entier "n":

	A vérifier avec des nombres.
· si n > 2, a ^n = a × a × …× a ( n facteurs "a")
· si n =1 ; a^1 = a
· si n =0 ; a^0 = 1
· si n > ou < 0 ; 0^n = 0
· si n < 0 ; si a ¹ 0

Quels que soient les nombres non nuls "a" et "b" , et quels que soient les entiers relatifs "n" et "p":

	A vérifier avec des nombres
a^n a ^p = a ^n +p
(a b)^n = a^n b ^n ; o u , (a b) ^p = a ^p b ^p
(a ^n) ^p = a ^n p

Les I.R. ( Identités Remarquables) Quels que soient les nombres "a" et "b":

(info cours)	A vérifier avec des nombres.
(a + b)² = a² +2ab + b²
(a -b) ² = a²-2ab+b²
(a + b)(a -b) = a² -b²

Remarque : il est plus facile de « développer » que de « factoriser » . Mais il est indispensable de savoir factoriser, pour, par exemple, savoir simplifier une fraction algébrique ou pour résoudre une équation.

V) Notations "scientifique" et "ingénieur" .

Notation des décimaux:

%  Scientifique : a× 10ⁿ avec 1< a < 10

%  Ingénieur : a ×10^p avec 1< a < 1000 et "p" multiple de "3"

Info .

RELATIONS D’ ORDRE

Info +

Relation d’ordre avec les décimaux relatifs.

Un réels « x » non nul est soit strictement positif ( on écrit x> 0) soit strictement négatif ( on écrit x < 0)

Le produit de deux réels de même signe est strictement positif.

Le produit de deux réels de signe contraire est strictement négatif.

La relation d’ordre est la relation «  ³ » par définition : x ³ y équivaut à x- y ³  0

La relation d’ordre est une inégalité simple et elle en possède les propriétés.

Autres Propriétés de la relation : ³

Quelque soient les réels « x » « y » , « z » , on a :

x ³  x	A vérifier avec des nombres
Si x ³ y et y ³  x alors y = x
Si x ³  y et y³ z alors x ³  z
x ³  y équivaut à x + z ³  y + z
Si x ³  y et z ³ 0 , alors x z ³  y z
Si x ³ y et z £ 0 , alors x z £ y z

Et

Si x< y et a<b alors x+a < y+b

Si : x < y et t > 0 ; x t < y t

Si x < y et t < 0 ; x t > y t

Info	Les INTERVALLES

Soient « a » et « b » des réels tels que a £ b

Un intervalle est l’ensemble R , noté ] - ¥ ; + ¥ [

ou l’un des sous ensemble suivants :

Ensemble des réels « x » tels que	Noté	Exemples :
a £ x £ b	[ a ; b ]
a £ x < b	[ a ; b [
a < x £ b	] a ; b ]
a < x < b	] a ; b [
a £ x	[ a ; + ¥ [
a < x	] a ; + ¥ [
x £ b	] - ¥ ; b ]
x < b	] - ¥ ; b [

L’intervalle [ a , b ] a pour centre 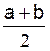et pour rayon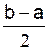

Lorsque a £ c £ b , on dit que « a » et « b » encadrent « c ».

Info+

Les encadrements sont des doubles inégalités ; Ils ont les mêmes propriétés que les inégalités simples : addition membre à membres des encadrements de même sens…….

Mais , comme pour les inégalités simples , on n’ a pas le droit de les soustraire ni de les diviser . Lorsque l’on veut encadrer une différence «  a - b » , on commence par encadrer (-b) puis la somme « a + (-b) , c’est à dire « a - b »

De même, pour encadrer un quotient , on encadre puis le produit , c’est à dire

D’un encadrement, on peut déduire un autre encadrement en agrandissant celui de départ, jamais en le diminuant.

Avant

VI) OPERATIONS SUR LES QUOTIENTS.

Après

Quels que soient les réels « a » , « b », « c » et « d » et tels que « b » et « d » soient non nul :

·

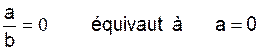
· n'a pas de signification pour b= 0

·En considérant des nombres a, b, c, m, n, x, y, z , t tous non nuls:

« égalité »
	Vraie si x t = y z
Simplification :
« produit »
Somme :
Savoir placer le signe « - »
Inverse
Quotient :

Info---

VII ) OPERATIONS SUR LES RADICAUX.

Info +++

·Racine carré : équivalences d'écritures : = = : lire: racine carrée de "x"

·Cas général : =

(Touches de la calculatrice : ; ; ; )

· Si a > 0, est le nombre positif tel que ()² = a

· L'équation x² = 5 admet deux solutions: et -

"3" est la racine carrée de "9" ; -3 son opposée.

(+3) et (-3) sont la racine carrée de (+9)

· pour l’équation x² = a , d’inconnue « x » (info +)

- elle n’a pas de solution si a < 0

- elle a pour seule solution « 0 » si a = 0

- elle a deux solutions et - si a > 0

· Règles de calcul

-si "a" "e 0 , = a ; (voir = )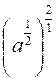

- ;

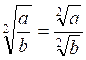
Où "a" et "b" désignent deux nombres positifs.

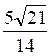= = (le dénominateur est sans radical)

·ConséquencesLvoir les IR)

( + ) ( - ) = a - b

(a+)² = a² + 2a + b

( - ) ² = a -2+b

· Ordre:

si 0 < a < b alors <

Info ++

EQUATIONS - INEQUATIONS

Et encore +

Info ---

Développer et Factoriser

Une expression algébrique dépendant d'une variable "x" , peut se présenter sous forme d'une somme ou d'un produit.

Suivant le problème que l'on cherche à résoudre , on aura intérêt à présenter (dans la mesure du possible) la même expression algébrique tantôt sous forme d'un produit, tantôt sous forme d'une somme.

· Pour présenter une expression algébrique sous forme d'une somme, on dispose des règles de calcul sur les nombres : "On développe" l'expression. Il est toujours possible, et simple de développer une expression, et une fois le développement effectué et réaliser, il est "d'usage" de "réduire" en effectuant les opérations chaque fois que possible, et "d'ordonner" l'expression obtenue, en rangeant les termes dans l'ordre des exposants de la variable.

· Pour présenter une expression sous forme d'un produit, on "essaye" de "factoriser". Il n'est pas toujours simple ni même possible, parfois, de factoriser une expression algébrique donnée. Par exemple, on ne factorise par une somme de carrés.

EQUATION DU 1^er DEGRE A UNE INCONNUE " x"

· L'équation de la forme a + x = b a pour solution unique x = b - a

· L'équation de la forme a x = b a pour solution unique x =

· Le principal cas particulier : "l'équation produit".

Exemple : (a x +b ) (c x - d )

On utilise dans ce cas le propriété suivante : un produit est nul si et seulement si l'un au moins des facteurs est nul.

Ainsi pour le produit (a x +b ) (c x - d ) est nul si (a x +b )= 0 ou (c x - d )= 0

Exemple algébrique ( 3x -1 ) ( (x-3) = 0

si le facteur (3x-1) = 0 (alors la solution est x = 1/3) ou le facteur (x-3) = 0 (alors la solution est x = 3 )

On conclut que : l'équation ( 3x -1 ) ( (x-3) = 0 admet deux solutions : 1/3 et 3.

Remarque : = 0 ; signifie A = 0 et B ¹ 0

SYSTEMES D' EQUATIONS A DEUX INCONNUES ( x ; y )

· Résolution par substitution.

Soit à résoudre le système défini par : (I)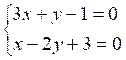

On a successivement (II)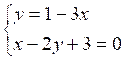

Dans la deuxième équation on remplace "y"par "1-3x" (III)

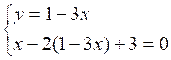
On développe et réduit dans la deuxième équation (IV)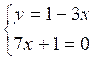

On en déduit "x" dans la deuxième équation: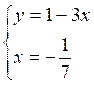

On remplace x = -1/7 dans la première équation : 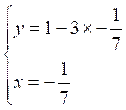d'où y = 1 + =

La seule solution du système 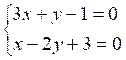est le couple de point :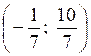

· Résolution par combinaison

Soit à résoudre le système défini par :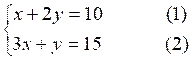

"cas 1" On multiplie l'équation (1) par -3 et "cas 2" puis l'équation (2) par -2

On obtient -3x -6y = -30

Ce qui donne :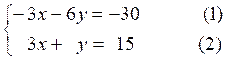

On additionne (1) + (2) soit -3x +3x -6y+y= -30 +15 ; -5y = -15 ; y = 3

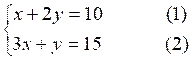On multiplie l'équation (2) par -2 ; on obtient -6x -2y = -30

-2 fois 3x + -2 fois y = -2 fois 15 ce qui donne -6x -2y = -30

on additionne (2) avec (1)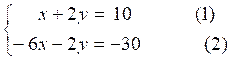

On addition l'équation (1) avec (2) ; on obtient -5x -0y = -20 ; x = 4

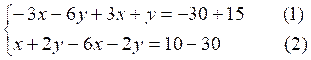soit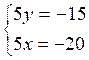

d'où l' unique couple de nombres solution ( 4 ; 3 )

· Résolution graphique du système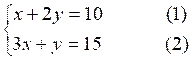

Il suffit de tracer les deux droites d'équations :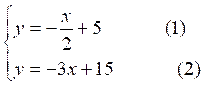

Le couple de nombres"solution" sont les coordonnées du point d'intersection des deux droites sont l'abscisse et l'ordonnée.

DROITES - FONCTIONS AFFINES -(inclus la fonction linéaire)

INFO+

Avant

· EQUATION D'UNE DROITE

Après

a) On connaît les coordonnées de deux points A et B :

Point : A ( 2;3) et point :B ( -3;1)

L'équation de la droite passant par le point A et B ; (AB) est de la forme y = m x +p. (1)

Des couples de points, on établit un système de deux équations:

On a

Après résolution on obtient : ;

On remplace dans (1) ce qui nous donne :

b) On connaît le coefficient directeur et un point :

L'équation de la droite est de la forme:

y = mx +p on donne m=-3 , A ( -1 ; 2)

On a y= -3x + p et +2 = 3+ p

D'où p = -1 et y = -3x -1

Avant

RESOLUTION D'UN SYSTEME D ' EQUATIONS INTERSECTION DE DEUX DROITES "D" et "D' "

Après

·.Il faut résoudre le système par les deux équations. (3 cas)

- Les droites sont sécantes, le système admet une solution.

- Les droites D et D' sont parallèles, le système n'a pas de solution. (aucun point commun).

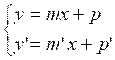si m=m' et p ¹ p' alors D // D'

- Les droites sont "confondues" (parallèles superposées), le système admet une infinité de solutions.

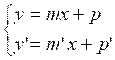si m=m' et p = p' alors D = D'

* Si mm' = -1 alors D ^ D'

Dans un repère orthonormal, deux droites sont orthogonales lorsque le produit de leur coefficients directeurs est égal à -1.

Avant

INEQUATIONS (système)

Après

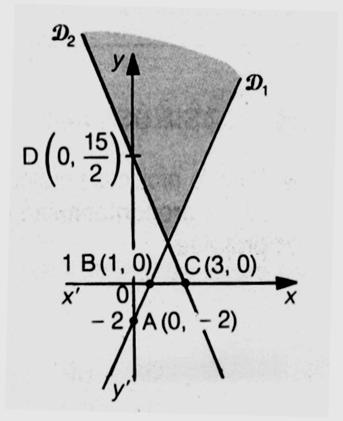
· RESOLUTION GRAPHIQUE D' UN SYSTEME D' INEQUATIONS A DEUX INCONNUES.

Présentation à partir de l'exemple: (I)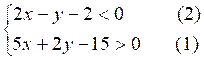

On traite et l'on trace l'équation (2) :

2x -y -2 = 0 ; y = 2x - 2 (droite D)

On traite et l'on trace l'équation (1) :

5x + 2y - 15 = 0 ; 2y = -5x - 15 ; y = -2,5 x - 7,5 (droite D')

Pour le point O (0 ; 0)

· 2 ´ 0 - 0 - 2= -2 ; -2 < 0 appartient à la région défini par (1)

· 5× 0 + 2 ´ 0 -15 = -15 < 0 ; 0 n'appartient pas à la région défini par (2)

La région colorée en gris est la zone contenant les solutions.

Fin du rappel : Retour vers liste

CONTROLE:

Cliquer ici

EVALUATION:

Cliquer ici.