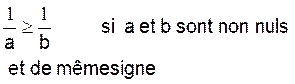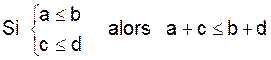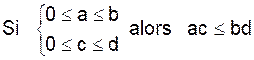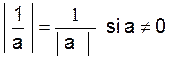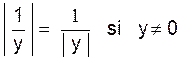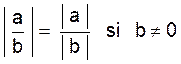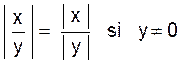Pré requis:
|
|
|
|
Les opérations avec les décimaux relatifs : Addition - Soustraction – Multiplication – Divisions –
Rationnels |
|
ENVIRONNEMENT du
dossier:
AVANT :
|
APRES :
|
Complément d’Info :
|
||
|
|
|
|
|
|
TITRE
: RESUME : TRAVAUX NUMERIQUES (
3è / seconde).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Travaux ; devoirs
|
|
Corrigé
|
|||
|
|
Contrôle |
évaluation |
|||
|
Interdisciplinarités : (matière concernée) |
||||||||
|
F |
H |
Géo. |
Vie quotidienne et vie familiale |
Autres : |
Sciences et technique
|
Physique Chimie Electricité |
Statistique. |
|
COURS
Un nombre peut - être
désigné de diverses façons. Lorsqu'on cherche une manière simple de désigner un
nombre défini par une certaine écriture, c'est en fait cette écriture que l'on
simplifie, et non le nombre donné sans ambiguïté par l'énoncé. Lorsqu'une
écriture contient des lettres, et désigne un nombre, chaque fois que les
lettres sont remplacées des nombres, on appelle cette écriture "expression algébrique" . Ex: 2x+5y-![]() z
z
|
I ) Rappels : LES ENSEMBLES |
On retiendra que :
N désigne l’ensemble
des nombres entiers naturels.
Z désigne l’ensemble des nombres entiers relatifs
D désigne l’ensemble
des nombres décimaux
Q désigne l’ensemble
des nombres rationnels.
R désigne l’ensemble
des nombres réels. ( les réels non rationnels sont dit
irrationnels.
En résumé : N Ì Z Ì D Ì Q Ì
R
|
Info . |
II
) RELATIONS D’ ORDRE |
Relation
d’ordre avec les décimaux relatifs.
Un réels « x » non nul est soit
strictement positif (
on écrit x> 0) soit strictement négatif ( on écrit x < 0)
Le produit de deux réels de même signe est
strictement positif.
Le produit
de deux réels de signe contraire est strictement négatif.
La relation d’ordre est la relation « ³ » par
définition : x
³ y équivaut à
x- y ³
0
La relation d’ordre est une inégalité simple et elle en possède les propriétés.
Autres Propriétés
de la relation : ³
Quelque soient
les réels « x » « y » ,
« z » , on a :
|
|
A
vérifier avec des nombres |
|
|
|
|
Si |
|
|
|
|
|
Si x ³
y et
y³ z alors x ³
z |
|
|
|
|
|
|
|
|
|
|
|
Si |
|
|
|
|
|
Si |
|
Et
|
Si
x< y et a<b alors |
|
|
Si :
|
|
|
Si |
|
Soit « a » ,
« b » , « c » et « d » quatre nombres réels
|
|
a £ b équivaut à |
A vérifier avec des nombres. |
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
||||||
|
|
|
|
||||
|
|
|
|
||||
|
|
||||||
|
|
|
|||||
Soient « a » et « b » des réels
tels que a £
b
Un intervalle est l’ensemble R ,
noté ] - ¥ ; + ¥ [
ou l’un des sous ensemble suivants :
|
Ensemble des réels « x » tels que |
Noté |
Exemples : |
|
|
|
|
|
|
[ a ; b [ |
|
|
|
] a ; b ] |
|
|
|
] a ; b [ |
|
|
|
|
|
|
|
[ a ; + ¥ [ |
|
|
|
] a ; + ¥ [ |
|
|
|
] - ¥ ; b ] |
|
|
|
] - ¥ ; b [ |
|
L’intervalle
[ a , b ]
a pour centre 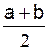 et pour rayon
et pour rayon 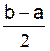
|
|
Lorsque |
►Les
encadrements sont des doubles inégalités ; Ils ont les mêmes propriétés
que les inégalités simples : addition membre à membres des encadrements de même sens…….
Mais ,
comme pour les inégalités simples , on n’ a pas le droit de les soustraire ni
de les diviser . Lorsque l’on veut encadrer une différence « a - b » , on commence par encadrer (-b) puis la somme
« a + (-b) , c’est à dire « a - b »
De même, pour
encadrer un quotient ![]() , on encadre
, on encadre ![]() puis le produit
puis le produit ![]() , c’est à dire
, c’est à dire ![]()
D’un encadrement, on peut déduire un autre
encadrement en agrandissant celui de départ, jamais en le diminuant.
►
« x » étant un nombre rationnel ou irrationnel ;
« x » peut être exprimé en valeur « a ± r » où « a » est une valeur approchée
de « x » à « r » prés
Ainsi :
« x » peut être compris entre
« a » et « a+r » soit
a £ x £ a + r
On
dira que : « a »
est une valeur approchée par défaut de « x » à « r près »
Ainsi :
« x » peut être compris entre
« a - r » et « a »
soit a -r £ x £ a
On
dira que : « a »
est une valeur approchée par excès de « x » à « r près »
Nous pouvons écrire l’encadrement ![]() , ce qui signifie que « a » est une valeur
approchée de « x » à « r près »
, ce qui signifie que « a » est une valeur
approchée de « x » à « r près »
|
Valeur absolue. |
Pour tous réels « a » et « b » , la valeur absolue
de « a » se note : ![]()
Dans l’intervalle [ a , b
] où
« a » et « b » encadrent un nombre « c » ,
la distance de « a » à
« b » se note : d
( a, b)
|
Pour tous réels « a »
et « b » |
A vérifier avec des nombres |
|
Pour tous réels « x »
et « y » |
A vérifier avec des nombres |
|
|
|
|
|
|
|
Si a ³0 ; |
|
Si x ³ 0 ,
alors |
|
|
|
Si a £0 ; |
|
Si x £ 0 ,
alors |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = b ou a = -b |
|
x = y ou x = - y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Suite à ce
qui a été vu dans « l’encadrement »
Pour tout réel « a » et tout réel positif
« r » , les énoncés suivants sont
équivalents :
|
|
|
|
d ( x, a) = r |
d ( x
, a ) £ r |
|
x = a - r ou x = a + r |
a- r £ x £ a + r |
|
x Î [ a - r , a + r ] |
x Î [ a - r , a + r ] |
|
|
Distance
. |
Attention : Ne pas confondre « mesure
algébrique d’un bipoint » et « distance entre deux bipoints. »
La distance
entre des réels « x » et « y » est , par
définition :
|
|
d ( x , y )
= |
|
Sur la droite D
de repère ( O , ![]() ) soient A et B les points d’abscisses
respectives x = ( - 3) et y = (+ 4) . On a d (x , y ) =
AB tel que d ( -3 ; +4) = AB
) soient A et B les points d’abscisses
respectives x = ( - 3) et y = (+ 4) . On a d (x , y ) =
AB tel que d ( -3 ; +4) = AB
Exemple : tracer une droite graduée et placer A , O et B.
|
INEQUATIONS
(système) |
||
|
|
|
·
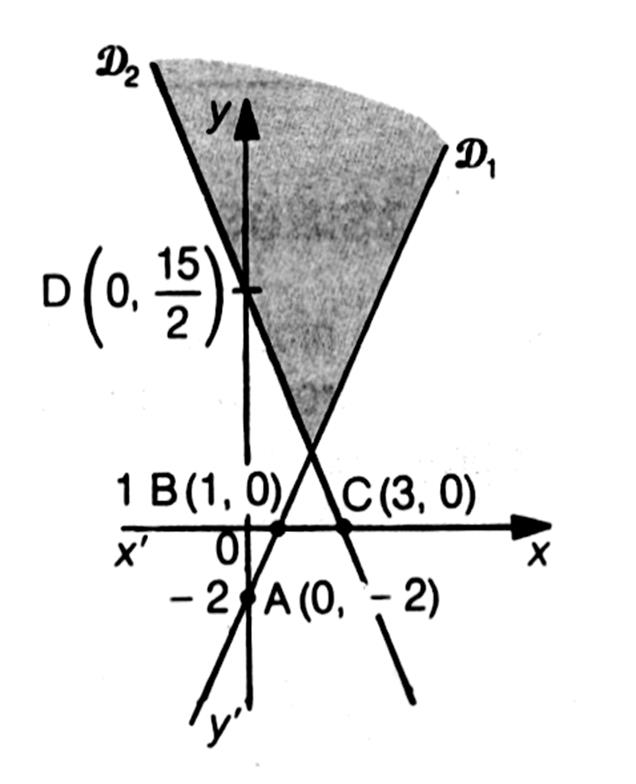
RESOLUTION GRAPHIQUE D' UN SYSTEME D' INEQUATIONS A DEUX INCONNUES.
Présentation à partir de l'exemple: (I) 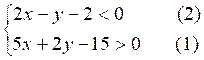
On traite et l'on trace l'équation
(2) :
2x -y
-2 = 0
; y = 2x - 2 (droite D)
On traite et l'on trace l'équation (1) :
5x + 2y - 15
= 0 ;
2y = -5x - 15 ; y = -2,5 x - 7,5
(droite D')
Pour le point O (0 ; 0)
· 2 ´
0 - 0 - 2= -2 ; -2 < 0 appartient à la région défini par
(1)
·
5× 0 + 2
´ 0 -15 = -15
< 0 ; 0 n'appartient pas à la région défini par (2)
La région colorée en gris est la zone contenant les
solutions.
|
Fin du rappel :
Retour vers liste |
|
|
Cliquer ici |
|
Cliquer ici. |