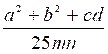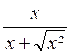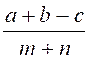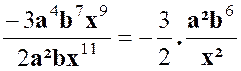|
|
|
ENVIRONNEMENT du dossier :
|
Objectif précédent |
DOSSIER : N°2 : ALGEBRE (Généralités)
définitions :
|
|
1°) Nombre algébrique : définition ; nombres algébriques égaux, nombres algébrique opposés. |
|
|
|
2°) Expression
algébrique : |
|
|
a)
Monômes entiers. |
|
|
|
|
b) Polynômes
entiers en « x ». (appelés aussi : sommes algébriques de
monômes) |
|
|
|
c ) Somme
algébrique de polynômes entiers en
« x ». |
|
|
|
d )Expressions algébriques
équivalentes. |
|
|
|
3°) Calcul
algébrique. |
|
|
COURS |
Interdisciplinarité |
|
|
Evaluation niveau
II |
|
|
Evaluation niveau
III |
|
|
1°)
Nombre algébrique : a) Définition Nombre algébrique (dit aussi : nombre relatif) : Un nombre
algébrique est un nombre arithmétique
précédé du signe plus ou moins . Voir "nombre
relatif" Un nombre algébrique est formé de deux
parties 1°) Un nombre arithmétique
, qui constitue sa valeur absolue (ce nombre arithmétique peut être
entier , décimal ou
fractionnaire. 2°)Un signe
, qui indique le sens de la grandeur mesurée ,
Précédé du signe + , le nombre est dit
positif : + 5 ; +2,8 ; +
Précédé du signe - , le nombre est dit
négatif : - 5
; - 2,8 ; - le nombre arithmétique qui figure
dans un nombre algébrique s’appelle sa « valeur absolue » b) Nombres
algébriques égaux : Deux
nombres algébriques sont égaux s'ils ont même valeur absolue et le même signe . Exemples : + 0,25 et + c) Nombres algébriques opposés: Deux nombres algébriques sont opposés s'ils ont la même valeur
absolue et sont de signes contraires . +7 ; -7 Ce sont des nombres relatifs de signes contraires Voir
"somme de nombres algébriques" Commentaire
:
La forme simplifiée d’une somme
algébrique est une expression
algébrique. En algèbre
,il n’est donné à traiter que
des expressions algébriques. |
|
|
|
|
|
|
|
|
|
|
|
2°) Les expressions
algébriques. |
|
|
|
Une expression algébrique est un
« assemblage » de lettres et de nombres par l’indication des
symboles d’opérations. Les expression
algébriques se présentent souvent sous une forme extrêmement compliquée. On doit , avant toute
chose , opérer des modifications d’écriture, ayant pour but de donner à
l’expression sa forme la plus simple. |
|
|
|
a)
Définition d’une expression
algébrique: Une expression algébrique est
un ensemble de nombres relatifs et de variables sur lesquels sont indiquées
des opérations à effectuer. Commentaire : La
forme simplifiée d’une somme
algébrique est une expression
algébrique. En algèbre, il n’est donné à traiter que des expressions
algébriques. Une expression algébrique est
un ensemble de lettres et de nombres reliés entre eux par les signes des opérations arithmétiques élémentaires,
de telle manière que, si l’on remplace chaque lettre par un nombre ,
les règles de l’arithmétique permettent
d’effectuer les opérations indiquées . Le résultat final du calcul est
dit la valeur numérique de l’expression pour les valeurs particulières données aux lettres .
On dit aussi :
Une expression algébrique est un ensemble de nombres (donnés
explicitement ou représentés par des lettres ) reliés par les signes des six
opérations. Exemples : |
|
|
2ax2
-8bx |
|
a - |
|
|
|
b ) Les expressions algébriques rationnelles. |
|
|
|
Lorsque l’expression est rationnelle , c'est-à-dire ne comporte pas l’indication
d’extraction de racines , de racines carrées ,par exemple, le but de
simplification d’écriture est acquis par l’application méthodique des
méthodes à voir dans le module
« calcul algébrique » Une expression algébrique
est dite "rationnelle" quand elle ne contient pas de lettres sous
un radical. Dit autrement: une expression algébrique est dite rationnelle lorsque , parmi les opérations à effectuer sur les nombres représentés par des lettres , il
n'y a aucune extraction de racine. Une expression rationnelle ne
comporte que des additions, soustractions, multiplications et divisions. |
|
|
|
c ) Expression algébrique irrationnelle: Une expression algébrique est dite
"irrationnelle" quand elle
contient une ou des lettres
sous un radical. (parmi les opérations à effectuer sur
les nombres représentés par des lettres , il y a une
extraction de racine.) Exemples : |
|
|
|
d ) Expression algébrique
rationnelle entière : Une expression algébrique rationnelle est dite "entière" lorsque , parmi les opérations à effectuer sur les nombres
représentées par des lettres , il n'y a pas de division. Exemple : ( a 2
+ b 2 ) (c 2 + d 2 ) |
|
|
|
e ) Expression algébrique
rationnelle fractionnaire : Une
expression algébrique rationnelle est
dite "fractionnaire" lorsque , parmi les
opérations à effectuer sur les nombres représentées par des lettres , il a une division. Exemple
: |
|
|
3°) Monômes entiers. |
|
|||
|
|
Le monôme est la plus simple des
expressions algébriques. Un monôme entier est constitué par un produit dont
les facteurs sont des puissances de la lettre (ou des lettres) sur laquelle
on décide de fixer son attention. D’autres
facteurs numériques ou littéraux interviennent aussi et constituent le
« coefficient » , lorsqu’on les a
ressemblés en un seul facteur. « - 3 a ² b ² x 5 » ; « Dans le
second , le coefficient est Le « degré » d’un monôme entier
par rapport à un lettre déterminée ,
est l’exposant de cette lettre. Ainsi :
« - 3 a ² b ² x 5 » est de degré « 5 » par
rapport à « x ». Le « degré » d’un monôme entier
par rapport à l’ensemble des lettres , est
la somme des exposants de ces lettres. Ainsi :
« - 3 a ² b ² x 5 » est de degré global : «
2 +2+ 5 = 9 » Si une
lettre n’a pas d’exposant, c’est comme si cet exposant était égal à un. On appelle
« mon^mes semblables », des monômes qui
ne différent que par leurs coefficients. Exemple « - 3 a ² b ² x 5 »
et « La somme
(algébrique) de deux ou plusieurs mon^mes sembles
est un monôme dont le coefficient est la somme des coefficients des monômes
donnés : Exemples 1 : « 17 x ²
- 13 x² + 11 x² = ( 17 – 13 + 11 ) x²
= 15 x² » Exemple
2 : « - 3 a ² b ² x 5 + · La multiplication de deux ou
plusieurs monômes entiers est tributaire de la règle de l’addition des
exposants. ( voir @ cours …) « - 3 a ² b ² x 5 .
4 a b 3 x 9 = - 12 a 3 b 5 x 14
» · Le quotient de deux monômes
s’opère par la règle de la soustraction des exposants. ( voir @ cours …)
|
|
||
|
|
Polynômes
entiers en « x ». |
|
||
|
|
On désigne
sous ce nom les sommes algébriques de monômes dans lesquels on a précisé que
l’on veut les envisager par rapport à la lettre « x » : |
|
||
|
|
|
P( x ) = 3 x 7- 8 x5 + 11 x 4 - P( x ) = - 5 a x 3 + |
|
|
|
|
|
|
||
|
|
L’ordonnation du polynôme est
l’écriture de ses différents termes par ordre d’exposants croissants ( ou décroissants) de la lettre « x », après
groupement des mêmes puissances de « x » , ou « réduction ». C’est le
cas des polynômes ordonnés suivant les puissances décroissantes de la lettre
« x », qui est le cas habituel. Le degré
du polynôme est la valeur de l’exposant le plus élevé de la lettre
« x ». Le polynôme : P (x) = 3 x 7 – 8 x 5
+ 9 a x + b. est du 7ème degré. |
|
||
|
|
|
|
||
|
|
On notera que dans
d’autres théories , un polynôme est seulement représenté par la suite
classé de ses cœfficients : P = ( 3 ; - 8 ; 9 a ;
b) pour l’exemple ci-dessus . Dans un
polynôme en « x » , la lettre
« x » qui peut prendre telle valeur numérique que l’on voudra ,
s’appelle « inconnue » , ou « la variable » . Le terme
qui ne contient pas « x » ( s’il y en a un
) s’appelle le terme « constant » : il est de degré zéro. |
|
||
|
|
|
|
||
|
|
d) Somme algébrique de polynômes entiers en « x ». (simplification ;
ordonnation ; …) |
|
||
|
|
|
|
||
|
|
Les
polynômes donnés sont écrits entre parenthèses ,
à la suite les uns des autres, les parenthèses étant précédées du signe de
l’opération ( addition ou soustraction) à effectuer. |
|
||
|
|
|
|
||
|
|
Procédure : 1°)
supprimer les parenthèses. 2°)
Réduire les monômes semblables , en même temps on
réalise l’ordonnation. |
|
||
|
|
Exemple :On donne 3 polynômes : P ; P ‘ ; P ’ ’ |
|
||
|
|
|
|
|
|
Nombres irrationnels ?
|
|
|
Rappel :
« Variable » : |
|
|
|
Définition d’une variable: Une variable
est une lettre, elle représente , généralement ,en sciences physique ,une
quantité qui peut prendre diverses valeurs. |
|
|
|
Voir : @
Expression et somme
algébrique. |
|
|
|
Expressions
algébriques équivalentes. On dit que deux expressions algébriques sont
"équivalentes" (ou identiques )
lorsque , en remplaçant dans les deux expressions chaque lettre par un même
nombre arbitraire , et en effectuant tous les calculs indiqués , on obtient
toujours deux résultats égaux. Ainsi,
considérons les deux expressions a 3 - b3 et
( a - b ) ( a2 -2ab + b2
) Elles sont
équivalentes parce que si l'on
remplace "a" par un nombre quelconque et "b" par un nombre quelconque
et si , dans ces conditions , on calcule la valeur
numérique de a3 - b3
et la valeur numérique de ( a - b ) ( a2 -2ab + b2
) On trouve
deux nombres égaux Exemple :
Remplaçons "a"
par « 5 » et "b" par « 2 » dans
les expressions a 3
- b3 et ( a - b ) ( a2
-2ab + b2 ) a3
- b3 = 53 - 23 = 125
- 8 = 117 ( a - b ) ( a2 -2ab +
b2 ) = ( 5 -2 ) ( 52-2 si nous remplaçons "a" par 10 , "b" par 1 : a3 - b3= 999 ( a - b ) ( a2 -2ab +
b2 ) = 9 On trouve
une nouvelle fois le même nombre . |
|
|
|
|
|
|
|
Le calcul algébrique a pour but de
remplacer certaines expressions
algébriques données par des expressions équivalentes . Pour cela il faudra maîtriser les
connaissances dispensées en FACTORISATION et DEVELOPPEMENT
. |
|
|
|
TRAVAUX AUTO FORMATIFS. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1°) Donnez la définition d’une
expression algébrique. 2° ) Donner
la définition de « variable » 3° ) Donner
la définition de « somme algébrique ». 4° ) Quelle
relation y a t - il entre « somme algébrique » et « expression
algébrique »? 5° ) Pour
faire du calcul algébrique ,que doit-on faire de l’expression algébrique ? 6°) Donner la procédure permettant de
transformer une expression algébrique en somme algébrique. I ) Remettre
sous forme relative les nombre suivants:
Remplacer les lettres par leur valeur et effectuer
le calcul si vous avez fait les opérations avec les nombres relatifs 1 ) Soit B = x - y Transformer l'expression en somme; faire le calcul:
2° ) idem que ci dessus:
Faire
le calcul des sommes
algébriques suivantes:
(montrer les étapes successives de transformation; l’utilisation de la calculatrice est
autorisée comme moyen de vérification ,mais
attention il faut bien connaître sa machine, elle peut vous donner un
résultat qui n’est pas conforme)
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||