|
Pré requis :
notions préliminaires sur le calcul algébrique… |
|
|
|
|
|
|
|
|
|
Pour + ‘info voir document « professeur ».
DOSSIER:
Cours N°1 : ALGEBRE (Généralités)
-
Signes et
lettres : emploi des lettres ; signes opératoires ;
coefficient ; le signe « multiplier » ; exposant ;
signes de relation ; les parenthèses ; l’énoncé ; formules.
COURS
L ' algèbre
existait bien avant l ' ère chrétienne.
Nous en trouvons
des traces sur des tablettes retrouvées sur le site de NIPPUR
( Babylone) , vieilles de quatre mille ans , et presque à la même époque
, en Egypte .
Puis ce fut à la Grèce , pépinière
de savants philosophes et mathématiciens
, de reprendre le flambeau de l ' algèbre avant de les transmettre aux nations civilisées les plus proches de
nous : , celles des Indiens , celles de
Arabes qui l ' introduisent en Europe au
moyen âge(vers 950).
En 825 , un
sage de Bagdad , al-Kharezmi , écrivit un illustre traité de mathématiques
intitulé AL-Djabr w a J
muqabalah ( l ' art d 'assembler et de
réduire des inconnues pour les égaler à
une quantité connue).De là est né le nom ALGEBRE.
L '
algèbre permet de réduire un problème
concret à une ou plusieurs égalités
simples où les nombres à découvrir sont
remplacés par des lettres que l
'on appelle des "inconnues".
D ' où " Résoudre
": la résolution d ' équations ou d
' inéquations , les calculs d
'expressions numériques ( exemple : 3 x2 - 7x +3 ) pour des
valeurs de x appartenant aux ensembles de nombres relatifs sont des problèmes relevant de l ' algèbre.
Algèbre
Préliminaire:
Dans une question
d'arithmétique le même nombre peut
représenter deux grandeurs différentes.
On peut , par
exemple, considérer
De plus , si
on a ensuite un problème analogue à faire , on sera dans l'obligation de
refaire sur les nouvelles données le
même raisonnement que l'on avait fait précédemment ,puisqu'on ne sait pas la
nature de la grandeur particulière représentée par chacun des nombres écrits ;
on ne pourra pas profiter des calculs antérieurs pour obtenir plus rapidement
le résultat.
Supposons maintenant
que , dans l'exemple précédent, au lieu de laisser les nombres , on convienne
de représenter par "a" le
nombre de mètres , par "b" le nombre d’euros que coûte chaque mètre ( à l' exclusion de tout autre signification) :partout où l'on
verra "a" , on pensera au nombres de mètres ; et partout ou
l'on verra "b" , on
pensera au nombre d’ euros .
Si dans la solution trouvée dans ces conditions on remarque
qu'il y a : b 
a ,cela voudra dire qu'il faudra multiplier le
nombre d’ euros par le nombre de mètre
et cela , dans tous les exemples
analogues , quels que soient d'ailleurs
les nombres représentés par "a"
et "b".
notation algébrique
La notation b
a équivaut à une phrase entière ; ce type de phrase est appelée "notation
algébrique"
La notation algébrique est une écriture qui utilise
des lettres et des signes opératoires traduisant une situation
mathématique .
But de l'algèbre:
L'algèbre a pour but la simplification et la
généralisation des questions sur les nombres:
L' algèbre a donc pour but :
1°) de simplifier les calculs.
2° ) de faciliter la résolution des problèmes.
3° ) de généraliser les résultats obtenus.
La simplification est due à l'emploi de signes pour indiquer
les opérations et , dans les problèmes , de lettres pour désigner les nombres cherchés.
La généralisation est due à l'emploi de lettres pour représenter les
nombres donnés.
SIGNES ET LETTRES UTILISES EN ALGEBRE.
0n désigne les
nombres (quantités ) par des lettres.
Autrement dit : les lettres servent à représenter les nombres.
Au lieu de raisonner, comme en arithmétique , sur des
nombres : « 4 » ; « 6 » ; « 
» ; etc , on raisonne sur des lettres :
"a" , "b" , "c",… »x » ,
« y »,…censées représenter des nombres connus ou « à
connaître ».Les résultats auxquels on parvient ainsi offrent une grande
généralité , car, comme on ne précise pas sur quels nombres on opère, ils sont
vrais pour tous les nombres.
Les premières lettres de l' alphabet "a" ,
"b" , "c", ….représentent ordinairement les nombres (quantités) connus.
Les nombres que l'on se propose de chercher sont désignés le
plus souvent par les dernières lettres de l'alphabet :
"x" , "y" , "z" …que l'on appelle les
nombres ( quantités )
"inconnues"
L'algèbre emploie les mêmes signes que l' arithmétique et quelques autres que nous aurons occasion
de définir au cours de la progression..
Nous rappelons brièvement les significations des signes de
l’arithmétique.
On a vu que les signes usités pour indiquer les opérations
sont :
1°) pour l'addition , le signe "+" il se
prononce : (plus) : l’ écriture « a + b » représente une addition , "la somme" est le résultat de l’addition désignés par "a" et
"b" ,comme 3 + 5 représente
l’addition des deux nombres 3 et 5. ( 8
est le résultat de l’addition ).
2°) Pour la soustraction , le signe " - " il se prononce (moins) : a - b
représente la soustraction des
nombres désignés par "a" et
" b" , comme 12- 7 représente
la soustraction des deux nombres 12 et
7. ( 5 est le résultat de l’opération , 5 est appelé la différence.)
3°) Pour la multiplication , le signe
" " il se prononce (multiplié par ):
Lorsqu’on représente les nombres par les lettres , on
emploie souvent le ‘point » , ou même on se contente d’écrire les deux
lettres qui représentent les nombres à multiplier l’une à la suite de l’autre
Sans intercaler un signe .
Ainsi , ab ; a .b ; et
ab représente le
multiplication du nombre désigné par "a" par le nombre désigné par "b"
comme : 3 7 représente la multiplication du nombre 3 par
le nombre 7 , « 21 » est le résultat de l’opération ,
« 21 » est appelé « produit ».
On simplifie la
notation , on supprime le signe "" entre les facteurs : abc équivaut abc ,il faut souvenir de cette convention dans les calculs
algébriques.
Cas particulier de la multiplication : On appelle « puissance »le produit de
plusieurs facteurs égaux. . L’exposant de la puissance est le nombre de
ces facteurs. Pour écrire une puissance, on emploie une écriture abrégée, qui
consiste à écrire une seule fois la valeur commune des facteurs égaux et à placer en haut à droite l’exposant .
4°) Pour la division , le signe " :" il se prononce (divisé par ): a : b
représente la division du nombre désigné par "a" par le nombre
désigné par "b" , comme 56 :4
représente la division de 56 par 4 .( le
résultat de l’opération est « 14 » , « 14 » est appelé
« quotient » . le résultat de la division est appelé
« quotient ».
En algèbre , on emploie de préférence la notation :
qui s'énonce
"a" sur "b" et qui équivaut à "a" : "b" ( on reverra la définition de ce qu’est
« une fraction » ) .
5°) Radical : Le signe
est le même qu’en arithmétique , c’est à dire qu’on écrira : 
ou 
pour « racine
carrée » de 8a et 
pour racine cubique
de 7b
Pour indiquer que l’on recherche une
racine d’un nombre , (on dit aussi
« extraire » , on utilise le signe 
, ce signe porte le
nom de "radical" .sous le
trait horizontal place le nombre dont on
doit extraire la racine ;
l' ordre de la racine
s'écrit au-dessus de l'angle
formé à gauche du signe . ( c’est généralement un nombre entier )
Le nombre qui
indique l'ordre de la racine s'appelle l '"indice du radical" .
Ainsi 
représente la racine
quatrième du nombre désigné par "a" , comme 
représente la racine quatrième du nombre "256" ,et le nombre "4" est ici l'indice du radical
.
Quand l 'indice du radical est 2 ou 3 , on dit comme en arithmétique " racine carrée ,
au lieu de racine deuxième , et racine cubique au lieu de racine troisième.
Quand l' indice est 2 et qu'il n'y a pas de radical ayant un
autre indice que 2 , on peut ne pas écrire l'indice.
Ainsi 
représente la racine
carrée de "a" , mais il faut écrire
+
et non pas +
On appelle "coefficient" un nombre ou une lettre
représentant ce nombre que l'on place devant une quantité pour indiquer le
nombre de fois qu'il faut répéter cette quantité .
C'est en somme l'indication
du produit de ce nombre par la quantité sans utiliser le signe "multiplier" () ; on dit aussi : que le coefficient est un nombre
qu’on place à gauche d’une lettre comme multiplicateur et après un signe + ou -
.
Exemples:
|
6a |
6 est le
coefficient de "a", cela veut dire 6 |
Cette écriture
remplace l' addition : |
|
5 ( +7) |
5 est le coefficient du nombre relatif (+7) |
(+7) + (+7) + (+7) + (+7) + (+7) |
|
mx |
m est le coefficient
de " x " |
L’écriture m x
signifie « m fois x »
,le’ signe « multiplier » ne s’écrit pas pour ne pas confondre « x » et le
signe » x » de la
multiplication , donc m |
|
|
|
|
|
Autre cas :
|
|
Info +:cliquer ici |
IMPORTANT : Le coefficient "1 " est toujours sous entendu:
|
Elément neutre dans la multiplication
: le "1" |
SOS cours: cliquer ici |
AINSI:
|
a |
1 est le coefficient de
"a" |
a = 1 |
|
x |
1 est le coefficient de
"x" |
x = 1 |
Par
convention ,en algèbre le signe « multiplier »
, « 
» n’ est jamais représenté pour éviter de le confondre avec
« x »
CONVENTIONS D’ECRITURE:
Dans les
expressions algébriques le signe
« multiplier » n ‘ est jamais
représenté
On ne trace pas
la « croix » pour éviter toute confusion avec la lettre
« x »,qui est couramment
utilisée pour représenter «
l’inconnue » .
En l’absence de signe ,il y a
toujours « produit » entre:
un nombre et une lettre :
3x ;lire « trois fois ixe »
(le mot
« fois » doit être remplacé
par « multiplié par »
)
deux lettres :
ab ; lire « a fois b » ou « a » facteur « b »
un nombre
et une racine: 3
;lire « 3
fois racine carré de 18 »
un nombre et une parenthèse :
3 ( 2x + 1) ; lire « 3 fois entre parenthèses 2 ixe plus un » ou
aussi « 3 facteur de 2ixe plus
un »
les groupes de mots « fois
entre parenthèses » et « facteur de » ont la même
signification .
une
lettre et une parenthèse: x ( 2x +2) , lire « ixe facteur de
2ixe plus 2 »
entre
deux parenthèses
: (2x+1)(3x+2) , lire
« 2ixe plus un » , entre parenthèses , facteur de « 3 ixe
plus 2 »
|
Pré requis
« calcul numérique ». |
La notation des
exposants , indiquée en arithmétique , est employée aussi en algèbre: a5 représente le produit de 5 facteurs égaux au
nombre désigné par "a" , comme 35 représente le produit de 5 facteurs égaux à 3 (3132333435 )
Ainsi : a5
s'énonce "a puissance 5" , 5 est l'exposant de la puissance.
On dit que "a" est élevé à la
5ème puissance.
On appelle "exposant" un nombre ou une lettre que l'on place en
haut et à droite d'un nombre , d'une lettre, d'une parenthèse ou d'un crochet
pour indiquer la puissance à laquelle on doit élever le nombre , la
lettre , ou la quantité placée entre parenthèses ou entre crochets , c'est à dire le nombre de fois que cette quantité
doit être multipliée par elle même.
|
Exemples: |
On
lira !!!!!! |
Ce qui
s’écrit aussi !!!!! |
|
52 |
Se lit :
5 exposant « 2 » ou 5 puissance 2 ou « au carré » |
52 = 5 |
|
a3 |
Se lit :
"a" exposant « 3 »
ou "a" puissance
3 ou « au cube » |
a3
= a |
|
(a-b) 2 |
Se lit :
(a-b) exposant « 2 » ou
(a-b) puissance « 2 » |
(a -b) 2 = (a -b) |
|
Attention !!! ( -5) ²
n’est pas égal à « - 5
² » ; on doit savoir
que « - 5² » est l ‘écriture simplifiée de - ( +5 ) ² |
||
|
A propos de
l'exposant 1 : par convention on
écrira 51 = 5 a1 = a x1 = x (a -b) 1 = (a-b) l’exposant « 1 » n’est jamais inscrit , mais il est parfois
utile de savoir qu’il « existe ». |
||
Terme algébrique .
On appelle « terme » une expression formée d’une ou plusieurs
lettres , ayant ou non un coefficient ,
et qui ne sont séparées par aucun signe
+ ou - .
Exemple : 4ab2 est un terme
On a vu
que les signes usités en arithmétique pour indiquer la relation qui existe
entre deux nombres sont :
1° ) Le signe = (égal à ) : a
= b indique que le nombre désigné par
"a" est égal au nombre désigné par "b" comme
8 + 2 = 10 indique que la somme des deux nombres 8 et 2 est
égale à 10.
a = b s'
énonce " a égal à b " ou "a égale b"
2°) le signe <
(plus petit que ) indique que le nombre placé à gauche de ce signe est plus petit que le
nombre qui est placé à droite du signe.
a<
b indique que le nombre désigné par
"a" est plus petit que le nombre
désigné par "b" , comme
1 + 3 < 5 indique que la somme
1+3 est plus petite que 5 .
a<
b s'énonce "a plus petit que
b".
On voit que le nombre
le plus petit est du coté du sommet de
l'angle.
3°) Le signe
> ( plus grand que ) indique que le nombre placé à
gauche de ce signe est plus grand que le nombre qui est placé à droite du
signe.
"a" >
"b" indique que le nombre
désigné par "a" est plus grand
que le nombre désigné par "b" , comme 12 - 2 > 9 indique que la différence 12 - 2 est plus grande que 9.
"a" >
"b" s 'énonce "a"
plus grand que "b".
On voit que le nombre
le plus petit est encore du coté du sommet de l 'angle , comme dans
l'emploi du signe précédent .
4° ) Le signe "¹ " ( différent de )
"a" ¹ "b" indique que le nombre
désigné par "a" est différent du nombre désigné par
"b" , comme 3 + 2 ¹ 1 + 6 , indique que la somme 3+2 est différente de la somme 1+6 .
5° ) Le signe £ ( inférieur ou au plus égal à )
: "a" £ "b" indique que le nombre
désigné par "a" est inférieur
ou au plus égal au nombre désigné
par "b".
"a" £ "b" s'énonce
: "a" inférieur ou plus
égal à "b" .( on voit ce signe
en arithmétique dans la théorie de la division euclidienne)
6° ) Le signe " ³ " ( supérieur ou au plus égal à ) :
"a" ³
"b" indique que le nombre
désigné par "a" est plus grand ou au moins égal au nombre désigné par "b".
"a" ³
"b" s'énonce : "a" supérieur ou au moins égal à
"b"
On emploie les parenthèses (…..)
, les crochets […..] ou entre « accolades :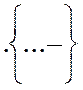 
pour indiquer que l'on considère comme effectuées les opérations à faire sur les nombres qui y sont renfermés.
Ce qui signifie que
lorsqu’on place une quantité entre parenthèses ( …crochets….,..) on indique par
là que cette quantité forme un tout « inséparable »
Lorsque l’on met
une opération entre parenthèses , on indique par là que l’opérations est
considérée comme « a effectuer » .
Ainsi ( a +
b - c) représente le nombre que l'on
obtient quand on a effectué le calcul indiqué par la notation a + b
- c
Alors si on a (a +
b ) (c + d ) ;
(a +b )
représente le nombre qui est la
somme de "a" et de "b" , que l'on désigne "A"
; ( c + d ) représente le nombre
qui est la somme de "c"
et de "d" , que l'on désigne "B" . On a donc une notation
de la forme "AB " , ce qui signifie qu'il faudra
multiplier A et B , c'est à dire
que (a + b ) (c + d ) indique
la multiplication du nombre " a+ b " par le nombre " c +
d ".
Il faut apporter
une très grande attention à l' usage des parenthèses ou des crochets. Leur
oubli dénature complètement l' opération à faire .
Exemples d'emploi de signes et lettres pour simplifier la
recherche de quantités.
Nous allons montrer comment
l'emploi de signes et de lettres pour
désigner les quantités simplifie la solution des questions sur les nombres .
Problème : Trouver
deux nombres , connaissant leur somme 40 et leur différence 12 .
Première approche : traitons la question par
l'arithmétique.
La somme des deux
nombres est égale au plus petit plus le plus grand ; or le plus grand est égal
au plus petit augmenté de 12 , qui est la différence entre les deux nombres ;
donc la somme des deux nombres est
égale au plus petit plus le plus petit
augmenté de 12 , c'est à dire 2 fis le plus petit plus 12 ; mais la somme est
40 , par conséquent 2 fois le plus petit
nombre plus 12 = 40; 2 fois le plus petit nombre vaut 40 diminué de 12 ou
28 ; une fois seulement le plus petit
nombre = 2 fois moins ou 14. Le plus petit nombre est 14 , le
plus grand est donc 26.
Vérification: la
somme des deux nombres 14 et 26 est bien 40 . Leur différence est de
12.
Deuxième approche : on reprend la même question en
indiquant les opérations par des signes et en représentant par la lettre "x" le
plus petit des deux nombres cherchés.
Le plus petit
nombre étant "x" , le plus grand est
"x+12 "
La somme des
deux nombres sera : x + x + 12
, ou 2x +12
Mais cette somme
est par hypothèse 40 , donc
on peut écrire:
2x + 12 = 40
|
retranchons « 12 » de part et d'autre : |
2x + 12 - 12 = 40 - 12
2x = 28
d'où x =14
Le plus petit nombre
est de 14 ,
le plus grand
est x +12 ou
14 +12 ou 26
La marche suivie dans
les deux cas pour résoudre ce problème
est absolument la même ; mais dans le premier cas , le raisonnement semble pénible à suivre , car il faut chaque fois se
souvenir de ce que l'on a dit précédemment , tandis que dans le deuxième cas ,
à chaque étape du raisonnement , on a sous les yeux les résultats successifs
auxquels on arrive peu à peu et qui constituent autant de jalons.
La
simplification de la recherche des
problèmes a été mise en évidence dans l'exemple simple où la
solution arithmétique était aisée. Cette simplification deviendra plus
manifeste dans la solution des problèmes où le raisonnement par l 'arithmétique
est long et compliqué.
Commentaire : Mais dans le résultat obtenu , il n'y a plus de trace des calculs que
l'on a effectué pour l'obtenir .Si on a
à résoudre de nouveau un problème analogue , il sera nécessaire de
refaire les mêmes calculs pour trouver le nombre cherché.
Nous allons montrer
que l'algèbre généralise les questions
sur les nombres et que cette généralisation est due à l'emploi de
lettres pour représenter les nombres
donnés avec leur signification.
ENONCE : (problème précédemment généralisé )
Trouver deux nombres connaissant
leurs somme "a" et leur
différence "b".
Ainsi on désigne "a" la somme des deux nombres cherchés et "b" la différence de ces deux nombres.
Soit "x"
le plus petit des deux nombres cherchés
, le plus grand est égal au plus petit augmenté de la différence , c'est à dire
de "b" ; le plus grand nombre sera
donc " x + b ".
La somme des deux
nombres sera donc : x + x + b
ou 2x + b ;mais
cette somme est désignée "a"
,
donc : 2x + b = a (1)
Retranchons "b" de part et d'autre : 2x + b - b = a - b
2x = a - b
d'où , en prenant la
moitié (en divisant de part et d'autre par 2 ) x =
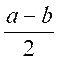
C'est
le plus petit des deux nombres. 2x + b =
a
Ajoutons "b" de part et d'autre , dans l'
égalité (1) , nous aurons
2x + b + b = a + b
2x + 2 b = a + b
d'où , en prenant la
moitié (en divisant de part et d'autre par 2 )
x + b = 
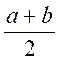; c'est le plus grand des deux nombres .
Donc si nous traduisons le résultat que l'on vient d'obtenir
, on écrira :
Le plus petit des
deux nombres cherchés s'obtient en retranchant la différence donnée de la
somme et en prenant la moitié du reste .
Le plus grand des
deux nombres cherchés s'obtient en
ajoutant la différence donnée à la somme
donnée et en prenant la moitié du total.
Commentaire: quels
que soient désormais les nombres donnés dans un problème de ce genre , on
pourra immédiatement , sans faire les opérations intermédiaires , calculer les
nombres cherchés.
FORMULES : Les expressions
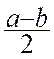et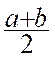 
qui donnent
les valeurs des deux nombres cherchés du problème précédent , s 'appellent des formules.
Une formule est l'expression des calculs
à effectuer pour arriver à la
solution numérique d'un problème déterminé .
Exemple : calculer l’intérêt d’une somme de 20 000
euros placés à 6 % , pendant 5 ans .
Solution voir
arithmétique : intérêt simple
En 1 an , le capital de 20 000 rapporte :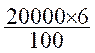
Et en 5 ans , il rapportera :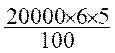 
Si l’on remplace Si l’on remplace le capital par la lettre
« c » , le taux par la lettre « a » , le temps par la
lettre »t » , et l’intérêt par la lettre « i » ,
on voit que l’on aura : i =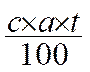 
Cette forme d’écriture est appelée « formule
algébrique »
Pour voir des exemples de formules ►
|
TRAVAUX AUTO FORMATIFS.
1.
Quels sont les buts
principaux de l' algèbre ?
2.
Donner un exemple de
notation algébrique :
3.
Qu'appelle -t -o n
notation algébrique ?
4.
En algèbre par quoi sont
désignés les nombres ?
5.
Que représente les
premières lettres de l' alphabet "a" , "b" , "c",
?
6.
En algèbre avec quelles lettres désigne -t -on les nombres cherchés ? comment les nommes t-
on ?
7.
Quels sont les signes
( 5 ) opératoires les plus usités en algèbre ;nommer l'opération ?
8.
Que représente les écritures
suivantes
|
a + b |
|
|
a - b |
|
|
a |
|
|
a : b |
|
|
|
|
|
|
|
9 .A quoi équivaut l'écriture algébrique
" abc"?
10 . A quoi équivaut l'écriture : ?
11 . comment s'énonce t elle ?
12.Comment appelle t on ce signe :
?
13. Qu 'appelle t on indice du radical ? (donner un exemple )
.
14 . L' écriture suivante "+" est interdite
pourquoi ?
15. Coefficients:
a) Qu' appelle t on "coefficient "?
b) Un facteur seul peut être précédé d'un coefficient ; lequel ?
16 .Que désigne les signes suivants ?
|
Traduire |
|
|
|
Le
signe = |
|
|
|
le
signe < |
|
|
|
Le signe > |
|
|
|
Le
signe "¹ " |
|
|
|
Le signe £ |
|
|
|
Le signe " ³ " |
|
|
|
17 . Traduire |
|
|
|
a = b |
|
|
|
a< b |
|
|
|
"a"
> "b" |
|
|
|
"a" ¹ "b" |
|
|
|
"a" £ "b" |
|
|
|
"a"
³ "b" |
|
|
Que peut on dire sur
la position des nombres situés à gauche
et à droite des signes : < et > ? :
LES PARENTHESES:
Qu 'indique
l'emploi de parenthèses et de
crochets dans le calcul
algébrique ?
Formule :
Qu'appelle- t -
on « formule » ?
Que signifie le mot résoudre une équation?
Nommer les coefficients :
|
|
Le coefficient est : |
Montrer l’opération: |
|
|
6a |
|
|
|
|
mx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
x |
|
|
|
CALCUL
ALGEBRIQUE
|
Devoir |