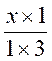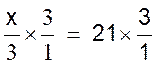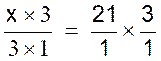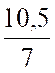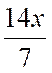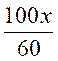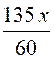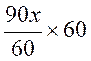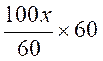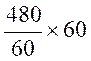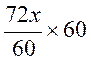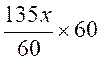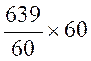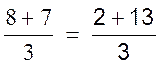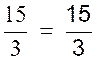Les
égalités neutralisation d’un terme et
d’un facteur en vue de résoudre
|
||
|
Les éléments et ensembles |
||
|
|
||
|
Définition de l’Objectif: Connaître et utiliser les quatre théorèmes de l’égalité., puis pour résoudre il faudra connaître les théorèmes de
transformation des équations. |
||
|
|
|
|
ENVIRONNEMENT
|
Objectif précédent : |
1°) Algèbre les conventions d’écritures. 2°) Suite. Et encore |
Retour au sommaire sur « les
égalités » |
DOSSIER:
|
|
LES EGALITES (n° 4/5) : les
4 théorèmes sur la
transformation d’une égalité.
|
|
|
|
|
|
|
|
Leçon importante à étudier pour savoir transformer les formules
mathématiques en sciences -physique
|
|
|
COURS |
Interdisciplinarité |
|
Activités interdisciplinaires proposées
:
|
|
|
|
Les
transformations d’égalités simples utilisées en mathématique et sciences |
q |
|
|
|
|
Les
égalités et les sciences ; en lien avec
les cours et problèmes |
q |
|
|
|
|
|
|
|
|||
|
|
COURS
|
|
|||
|
|
|
|
|||
|
|
Objectif du
cours sur les égalités :
Connaître ( énoncer ) et savoir
utiliser les quatre théorèmes de l’égalité.,
puis pour résoudre
une égalité on devra connaître les théorèmes de
transformation des équations.
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
Théorème N°1:
|
|
|||
|
|
On peut ajouter un même nombre ou un même terme aux
deux membres d’une égalité. *on dit que
l’égalité reste "vraie".
|
|
|||
|
|
|
|
|||
|
|
Rappel: en mathématique le mot
« ajouter » est toujours associé au
signe « + »
On dit aussi : que
l' On peut ajouter l'opposé d'un terme,
dans les deux membres de l'égalité . ( en vue de neutraliser
ce terme). Commentaire : ce théorème est utilisé pour
neutraliser un terme dans un membre, en effet ,on
neutralise un terme en ajoutant son opposé .,mais attention si l’on ajoute un
terme dans un membre il faut ajouter
le même terme dans le second membre
pour que l’égalité reste vraie. |
|
|||
|
|
Exemples
d’applications :
|
|
|||
|
|
Voir : recette
|
|
|||
|
|
|
|
|||
|
|
Exemple de transformation n° 1: |
|
|||
|
|
|
|
|||
|
|
Soit l’égalité je peux ajouter
mais pour que
l’égalité reste vraie je dois ajouter
3 au deuxième membre de
l’égalité. alors l’égalité devient:
commentaire : l’égalité reste
vraie puisque le calcul nous donne 18
= 18 |
|
|||
|
|
Exemple de transformation n° 2 : |
|
|||
|
|
|
|
|||
|
|
Soit l’égalité je peux ajouter
3 au premier membre de l’égalité ,il faut alors
le même terme au deuxième membre l’égalité précédente devient:
Commentaire: si l’on fait
l’opération possible on remarque que
le « 3 » du premier membre
disparaît; ainsi l’égalité se trouve
transformée:
|
|
|||
|
|
Exemple de
transformation n° 3 :
|
|
|||
|
|
(
on veut « x » tout seul … :
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
Transformations L
et calculs
|
|
||
|
|
|
L’équation :
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
On transforme l’écriture :
|
Devient
|
|
||
|
|
|
|
|
||
|
|
En écriture ci-contre (
appelée :somme algébrique )
|
|
|
||
|
|
|
|
|
||
|
|
On doit faire « disparaitre le ( + 5 )
|
|
|
||
|
|
|
|
|
||
|
|
Pour cela , on ajoute l’opposé de ( + 5)
= (-5)
dans le premier membre ;
|
Puis
s’écrit :
|
|
||
|
|
|
|
|
||
|
|
Mais
pour que l’égalité reste vraie on doit
ajouter le même nombre dans le deuxième membre ……
|
(x ) + ( + 5) + (-5) = (+ 12)+ (-5)
|
|
||
|
|
Dans
le premier membre on calcule : ( + 5) + (-5) = 0
|
On obtient ensuite :
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
Après
simplification on obtient :
|
|
|
||
|
|
|
|
|
||
|
|
Puis on calcule :
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
Conclusion :
on obtient la valeur numérique de « x » qui permet de trouver qu’ avec la valeur +7
l’égalité est vraie…..
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
Pour
simplifier on peut écrire :
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
Vérification : 7 + 5 =……………….. = 12
|
|
|
||
|
|
|
|
|
||
|
|
Conclusion
n°2 : x = 7
est la solution de l’égalité ….
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|||
|
|
Théorème N°2
|
|
|||
|
|
On peut
retrancher un même nombre ou un même terme
aux deux membres d’une égalité.
On dit que
« l’égalité reste vraie ». |
|
|||
|
|
|
|
|||
|
|
Exemples d’applications du théorème n° 2 : |
|
|||
|
|
Exemple N°1
soit l’égalité 10 + 5 = 15 exercice: Supposons que je décide de soustraire « 3 » au premier membre. je peux retrancher
« 3 » au premier terme
de l’égalité ; mais je suis obligé de faire de même dans le deuxième membre ,pour que l’égalité reste vraie: 10 +
5 - 3 =
15 - 3 l’égalité reste vraie si je fais le calcul, ,je remarque que j’ai bien 12 est égal
à 12
|
|
|||
|
|
|
|
|||
|
|
Exemple
N°2 : soit l’égalité: c +
3 = b exercice : je décide de soustraire « 3 » au premier membre,
dans ce cas je dois faire de même dans la deuxième membre
,pour que l’égalité reste vraie. : c +
3 - 3 =
b - 3 si je
simplifie (c’est à dire que j fais le calcul possible),j’obtient l’égalité suivante: c
= b - 3
|
|
|||
|
|
|
|
|||
|
|
Exemple
3 :
|
Transformations L et calculs
|
|
||
Procédure :
|
|
||||
On
ajoute - 5
|
|
||||
On
calcule : 5
- 5 = 0
|
|
||||
|
|
|
|
|
||
|
|
On
calcule 12 –5
|
|
|
||
|
|
|
|
|
||
|
|
Conclusion :
|
|
|
||
|
|
|
|
|
||
|
|
Commentaire : la plupart
du temps ce cas est traité différemment ; on transforme l’expression en
somme algébrique , il suffit alors d ‘ajouter
au nombre son opposé
|
Important : la
soustraction n’existe pas avec les nombres relatifs ,
il faut toujours transformer l’expression algébrique en somme algébrique, et
ajouter l’opposé du terme que l’on veut faire passer dans l’autre membre.
|
|
||
|
|
|
|
|||
|
|
THEOREMES : APPLICATIONS
|
|
|||
|
|
|
|
|||
|
|
A partir des exemples précédents on
peut apprendre et appliquer les
« recettes » suivantes et que l’on nomme des « corollaires »: Attention : ce ne sont que des
recettes , elles ont des limites et tous les
exercices d’algèbre ne peuvent être
résolus avec ces méthodes ! ! ! ! Corollaire N°1 : Tout terme
d’une égalité qui change de membre
change de signe. (cela découle du théorème 1
) |
|
|||
|
|
ainsi
l’égalité
|
|
|||
|
|
AINSI: |
|
|
||
|
|
|
Devient la somme
|
|
||
|
|
Transformation:
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
Commentaire
: Le terme « - 3
» passe du premier membre dans le deuxième membre
,alors « -3 »
du premier membre devient « +3 » dans le deuxième membre. autre exemple: l’égalité Commentaire: Dans une égalité ,on
peut faire passer un terme d’un membre dans l’autre ,à condition de
changer son signe. ATTENTION : dans ce cas le terme n'est que la valeur numérique ,cela pose parfois des problèmes , il est
préférable de passer par la somme algébrique.
|
|
|||
|
|
Méthode préconisée
|
|
|
|
|
|
|
|
Il faut passer par une étape intermédiaire :
|
|
|
|
|
|
Exemple
|
|
|
|
|
3x +15
= 25
|
Il faut transformer l’expression en somme algébrique
@
|
|
|||
|
|
(+3x)+( +15) = (+ 25)
|
|
|||
|
|
|
|
(+3x) = (+ 25) +( -15) 3x = ( + ( 25 – 15)) 3x = (+10)
|
|
|
|
|
Autres
transformations possibles (pas très utiles) |
|
|||
|
|
1°) 3x +15 = 25 ; on fait
passer « 3x » dans le second
membre ! devient 15
= 25 - 3x qui peut devenir 15 -25 = - 3x nous obtenons l’égalité - 10 = - 3x « problème : le signe - dans les deux
membres ; que l’on résoudra en multipliant les deux membres par
« -1 » , on obtiendra en fin de compte
l’égalité : 10 = 3x
|
|
|||
|
|
|
|
|||
|
|
2°) 3x + 15
= 25 on fait passer « 25 » dans le
premier membre ! l’égalité devient 3x+15 - 25 = 0 qui peut devenir par l’addition des nombres : 3x
- 10 = 0 |
|
|||
|
|
Rappel : pour faire
le calcul 15 - 25 ,il
faut transformer l’expression « 15 – 25 » en une somme algébrique
(+15)+(-25) ; et voir l’opération
(+15)+(-25);qui est l’ addition de
deux nombres relatifs de signe contraire .
|
|
|||
|
|
|
|
|||
|
|
La
transformation idéale : il faut
conserver les « x » positifs dans le premier membre et mettre toutes les valeurs
numériques dans le second membre !
|
|
|||
|
|
|
|
|||
|
|
Commentaire :
Toutes les transformations ,précédentes , sont vraies,
La « meilleure »
transformation est fonction du
résultat recherché, Celle
qui est intéressante est celle qui a
permis d ’
isoler le terme contenant les « ixe »,en vue de rechercher la valeur de « ixe »
:(
voir l’objectif: résoudre une équation EG3.)
|
|
|||
|
|
|
|
|||
|
|
Recette N° 2 : On peut supprimer un terme
commun aux deux membres d’une égalité, ( l’égalité reste
vraie) |
|
|||
|
|
Exemple : soit
l’égalité 15+ 3x + 3y
= 35 + 2x +3y On remarque que dans l’égalité que les deux membres ont « 3y » comme terme commun, on
peut donc supprimer les termes
communs, l’égalité devient donc: 15 +3x = 35 + 2x |
|
|||
|
|
ADDITION de deux
égalités : *si nous avons deux égalités , nous pouvons additionner les premiers membres
entres eux et les deuxièmes membres entre eux ,la nouvelle égalité reste
vraie. Exemple: |
|
|||
|
|
soit l’égalité (1)
|
|
|
|
|
et l’égalité (2)
|
|
|
|||
|
|
|
|
|||
|
|
addition (1) +(2) donne :
|
19x + 12
= 5 x + 1 |
|
|
|
|
|
15 x + 4 x = 19 x
|
|
2x + 3x = 5 x
|
|
|
|
|
9 + 3 = 12
|
|
5 – 4 = 1
|
|
|
|
|
|
|
|
|
|
|
|
Utilisation et
intérêt : voir la résolution d’un système d’équations :
|
|
|
||
|
|
|
|
|||
|
|
On peut multiplier les membres d’une égalité par un même
nombre, ou facteur(s),non nul. |
|
|||
|
|
Commentaire: cela revient à multiplier tous les termes de
l’égalité par ce même nombre ou même facteur(s),l’égalité
reste vraie.
|
|
|||
|
|
Exemple: 1
soit l’égalité: 8 + 7
= 2 +
13 je peux ,
par exemple , multiplier les 2
membres par « pour obtenir un résultat je devrais développer ( voir
Cours : « développer » ) autre possibilité: «multiplier les deux
membres d’une égalité cela revient à multiplier tous les termes de
l’égalité » ; alors dans
ce cas le résultat donnera directement: (a)
(8) + (a) (7) =
(a) (2) + (a) (13)
on écrira le résultat de façon plus
« élégante » 8
a + 7 a = 2
a + 13 a autre exemple: (on multiplie les deux
membres par un nombre)
soit l’égalité: 8 + 7
= 2 +
13 je peux ,
par exemple , multiplier les 2
membres par « 3 » , sans modifier l’égalité
, …………………l’égalité reste vraie: 3 ( 8 + 7 ) =
3 ( 2
+ 13 ) pour obtenir un résultat je devrais développer ( voir
Cours : « développer » ) autre possibilité: «multiplier les deux
membres d’une égalité cela revient à multiplier tous les termes de
l’égalité » ; alors dans
ce cas le résultat donnera directement: (3)
(8) + (3) (7) =
(3) (2) + (3) (13)
on écrira le résultat de façon plus
« élégante » 24 + 21
= 6 + 39 on
additionnera pour se rendre compte que l’égalité est encore
« vraie »
. ( faites les additions ) !!
|
|
|||
|
|
Exemple
2 : Résoudre |
|
|||
|
|
|
Procédure :
|
|
||
|
|
Se
rappeler que : SOS COURS
|
on
multiplie X/3 par 3/1 ; pour neutraliser le « 3 », mais il
faut multiplier le deuxième membre « 21 » par « 3/1 »
Après calculs
ou simplifications , on obtient : x =
63
|
|
||
|
|
|
||||
|
|
Remarques: Je peux multiplier tous les termes d’une égalité par
« -1 »
,cela à pour conséquence de changer
tous les signes qui précédent les termes. |
|
|||
|
|
APPLICATION
algébrique:
|
|
|||
|
|
|
|
|||
|
|
On
a transformé l'égalité
|
Pour devenir une égalité équivalente:
|
|
||
|
On veut faire disparaître le dénominateur: Il suffit de multiplier tous les termes par le nombre 7 |
|
||||
|
Après
calcul :on obtient l'égalité suivante: 3x + 10,5 = 14x
|
||||
|
|
|
||||
|
|
Autre exemple :
|
|
|||
|
|
|
|
|||
|
|
Pour passer de l’égalité suivante
à l’ égalité équivalente: 90 x- 100x + 480 = 72x - 135 x + 639 il faut multiplier tous les termes de l’égalité par le même
nombre : « 60 » (voir multiplication d’une fraction par un nombre)
les « 60 » s’annulent pour chaque terme |
|
|||
|
|
Nous obtenons bien l’égalité : 90 x- 100x + 480 = 72x - 135 x + 639
|
|
|||
|
|
|
|
|||
|
|
On peut diviser les deux membres
d’une égalité par un même nombre ,non nul . "l'égalité
reste vraie" |
|
|||
|
|
|
|
|||
|
|
Commentaire:
cela revient à diviser tous les termes de l’égalité par ce même nombre,(on peut dire aussi facteur(s) ). Exemple: Soit l’égalité: 8 + 7
= 2 +
13 je
peux diviser l’égalité par 3 dans ce
cas j’écrirai ou je
pourrai écrire l’égalité
reste « vraie » si je divise
les deux membres d’une égalité par la
même valeur (ou quantité) Application algébrique : soit
l’équation type : |
|
|||
|
|
|
Exemple numérique
|
Modèle théorique :
|
|
|
|
|
|
|||
|
|
Si
3 a = 15 ,pour
obtenir la valeur de " On divise par "3" chaque membre
1 a = 5
a = 5 il faut vérifier si 3 fois 5 = 15 |
Si
On veut "a" ,
on divise les deux membres par "b"
après simplification: a =
|
|||
|
|
|
|
|
|
|
|
|
Activité :
Procéder de la sorte si l'on cherche " b"
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|||
Devoir
sur les transformations de formules
|