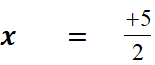Dossier 2 / 5  :

La Transformations d’ une  EGALITE :

Apprendre  à   « NEUTRALISER » un élément dans un membre d’une égalité.

( tout en conservant l’égalité vraie…)

1.     NEUTRALISATION d’un terme, dans un membre

2.    NEUTRALISATION d’un facteur , dans un terme

COURS.

Ces leçons sur ces « égalités » sont très importantes ……………………..Le but de ces travaux sur les égalités vont permettre de savoir comment transformer une formule  « mathématique » en vu de trouver un résultat………..numérique …

OBJ : connaître  les éléments neutres et les éléments absorbants ;  savoir neutraliser un terme ou un facteur dans un membre d’une égalité en vue de «  résoudre une équation   ».

Commentaire: 

On utilise la neutralisation pour transformer une égalité. (ou une inégalité)

Rappel : sur la signification du mot « RESOUDRE  @ » :

« Résoudre "une équation" »   c ' est rechercher la valeur de l ' inconnue (généralement ""

@  )   qui vérifiera    que l ' égalité est vraie.

( l’égalité est vraie lorsque l’on a remplacé « x » par la valeur numérique  trouvée  et effectué les calculs avec la valeur  de « x » ; il faut trouver la même valeur pour chaque membre , après calcul )

pour « résoudre » ;  on nous donne une égalité contenant une lettre appelée « inconnue ».

( exemple :   2  + 12 = 17  )

La  lettre «  » se trouve être un facteur « intégrer » dans un terme.

Résoudre : c’est isoler « x » dans le premier membre de l’égalité pour obtenir      x = .........

Pour cela il faut :  « isoler »  le terme contenant l ‘  «  »  ( cela revient à  éliminer le  terme qui ne contient pas de «  » , c’est sûrement un nombre)

Il faut donc neutraliser le  ou les  autres termes qui ne contiennent pas d’ » »  (Exemple :on doit  faire disparaître du premier membre    le  « +12 »  de :  

L’égalité         pour avoir   la nouvelle égalité , après simplification :  

Lorsque le terme en «  »  est « isolé »  il faut neutraliser le   facteur  associé   à «  » ( ici : 2 ) ;

pour n’ avoir que   «  » =

     Ainsi  on transforme    l’égalité         

     en une autre  égalité        ;que l’on peut aussi écrire : 

   ou    «  » 

Pour ce faire on a divisé  « 2x » et « 5 » par « 2 »………………l’égalité reste vraie ………

I)                 NEUTRALISATION D’UN TERME :

Exemple :          je veux résoudre l'équation       ;

Je dois donc « isoler »   le   « x » ,pour cela il faut  faire disparaître  le « +3 »  qui se trouve dans le premier membre.

Pour neutraliser le « +3 »  qui se trouve dans le premier membre ;   j'ajouterai   « -3 »  dans chaque membre tel que :

   ,

j'obtiens  la nouvelle égalité   x + 0 = 2 ; la solution de l'équation est  

Rappels: L'élément neutre de  l'addition et la soustraction est 0  ; sur la définition du mot "terme" :  les nombres situés à droite et à gauche du signe « +l »  s ’ appelle des termes) ; voir aussi : la somme des  nombres relatifs symétriques et égale à 0s .

             ( +5 ) + ( -5) = 0

On dira que vouloir :

       « neutraliser un terme ou un nombre précédé d’un signe + ou - »  , c’est  remplacer ce terme par « zéro »,

Pour cela il faut respecter la procédure suivante :

Procédure permettant de neutraliser un terme dans une égalité:

             Pour neutraliser un terme dans un membre ,   il faut et il suffit d’ajouter , dans ce membre ,son opposé  , mais attention  pour conserver l’égalité « vraie » il faut  l’opposé  dans les deux  membres de l’égalité.

Voir impérativement l’objectif  :@ OPP ET INV.: savoir écrire l’opposé et l’inverse d’un nombre donné.

Commentaires :

On neutralise un « terme dans un membre »  dans le but de ne laisser dans ce membre que le  terme qui contient la variable.(en vue de trouver la valeur numérique de cette variable .)

DIT AUTREMENT : La neutralisation sert à « isoler  » le terme contenant  comme facteur une lettre.

Dit Plus simplement:

Neutraliser des termes (dans un membre)est la première étape  permettant de « résoudre une équation ».

Ce qui suit est un exercice complètement résolu (Pour la compréhension)

Enoncer de l’exercice            :Résoudre l’équation   

Commentaire :           « résoudre l’équation »   c’est rechercher la valeur de X qui vérifie l’égalité.

Résolution:

Dans le premier membre nous avons deux termes ,un contenant     ,l’autre  la valeur  +12

 si nous voulons    seul ,nous devons faire disparaître le terme  12    ,on dit que l’on veut neutraliser  le terme  (+12 );

D ’ après la règle :  pour neutraliser un terme on lui ajoute son opposé

(l’opposé de +12    est        -12  ).

  +12 +  opp .(+12) =

Je vais donc ajouter au premier membre le terme « opp.(+12) » et ;pour que l’égalité reste vraie je devrai ajouter au deuxième membre l’opp.(+12).

Aussi l’égalité        devient l’égalité:

Rappel :    (opp.(+12) est égal à (-12)

L’égalité devient:

.On sait qu’un nombre ajouté à son opposé est égal à 0,dans le premier membre ne reste donc que le terme contenant  ;

on dit que l’on à isolé le terme (ou les termes) contenant

Nous avons la nouvelle égalité:

le terme 0 peut disparaître:

Il ne reste plus qu’à calculer  17 +(-12)  qui donnera comme résultat  +5.

On écrira alors comme réponse:

Vérification :après chaque calcul une vérification s’impose pour cela il suffit de remplacer  X dans l’équation de départ par la valeur  de X trouvée (ici +5) est faire indépendamment l’opération demandée dans le premier membre (  (+5) + 12 )= 17 ) ,ensuite l’opération  demandée dans le deuxième membre ( ici le calcul n’est pas à faire puisque nous avons un seul nombre: 17) et conclure en comparant les résultats.

Vérification:

premier membre   X + 12   devient  (+5) + 12  =...résultat du calcul  17

Deuxième membre     17    (dans ce cas il n’y a pas de calcul)

Comparaison du premier membre avec le deuxième membre  17 = 17   

Conclusion:

l’égalité est vérifiée  « vraie »,la valeur de X qui vérifie l’équation est +5

Série 1

Procédure : il faut transformer l’expression en somme ; ajouter au 2 membres l’opposé du terme à neutraliser ( pour obtenir « x + 0 » )

Série 2

Série 3

Cas : « » est dans le membre.

Série 4

Cas particulier : il y a un signe  « - » devant « x » 

Info plus

II) NEUTRALISATION D’UN FACTEUR

Nous venons de voir comment « neutraliser un terme »,en vue de résoudre une équation ,

Nous allons voir le cas où  «   » est associé à un  facteur « nombre » ( par exemple :  ).

Rappel:

L’élément neutre de la multiplication et de la division est 1.

Un nombre multiplié par son inverse est égal à     1

                            a  x   =    1

1°) Neutraliser un facteur:

Neutraliser un facteur (nombre ou lettre(s) ) dans un terme  d’un membre d’une égalité c’est le remplacer par la valeur   1 .

2°) Procédure permettant de neutraliser un facteur:

Pour neutraliser un facteur il faut et il suffit de multiplier ce facteur par son inverse.

3°) APPLICATION

a ) Neutralisation du nombre «  » dans le produit «  »

Procédure : 

Pour neutraliser le facteur «  » dans le produit de «  » il suffit de multiplier « » par «  »

Exemple :

Prenons l’égalité , on dit aussi :

On nous donne l’égalité :      

L’énoncé en algèbre serait  : quelle est la valeur de « x » qui vérifie l’égalité donnée.

Je veux      = ?

Je dois faire disparaître  « 2 »

C’est une multiplication !

je dois trouver un moyen de remplacer « 2 » par l’élément neutre « 1 » ; pour se faire  je dois multiplier « 2 » par son inverse.       ( lire : un demi)

1°)  Je multiplie « 2x » par   

( est l’inverse de 2 :   SOS Cours ? ??)

 fois    =  2    =   1 fois «  » ;   1 fois «  »  =

2°)  Pour que l’égalité reste « vraie » je dois multiplier le deuxième membre ( 17 )   par

17 fois   =    8,5

Conclusion :

Pour en savoir plus  aller en algèbre :  ( info +   ) 

En algèbre on nous demande de résoudre l’équation 

(ce qui  correspond au problème posé  : trouver la valeur de « x » qui vérifie l’égalité « vraie » )

III )  Cas où l’on doit , pour obtenir une égalité de la forme «  »,  appliquer les deux neutralisations précédentes :

Cas simple :       un  des  membres contient au minimum 2 termes ; le facteur « x » est multiplié par un nombre :

        «  »  

On désire obtenir ; après transformation  une équation de la forme «  x = …… »

Début de la résolution:

1°)D’après l’exemple précédant ,nous isolons le terme contenant «  »

devient:     2   + 12 + opp.+12 = 17 + opp +12

devient      2  +12  -12            = 17 -12

Exécution des calculs numériques:

on remplace dans l’égalité précédente:

Simplification:

   à ce niveau nous avons isolé le terme contenant X ;la résolution n’est pas terminée, il reste à isoler  X ,il faut donc neutraliser le facteur  « 2 »

de telle  sorte nous ayons         .(de ce coté du signe égal ne doit rester que des chiffres)

........................................(exercice à terminer ,voir suite page:........)

Cas complexe   :          un  des  membres contient au minimum 2 termes ; le facteur «  » est multiplié par un nombre :

        «  »  

procédure : il faut regrouper dans chaque  membre  les nombres ; ensuite il faut faire passer les « x » dans un membre  et les nombres dans l’autre membre.

Neutraliser un facteur:

Neutraliser un facteur (nombre ou lettre(s) ) dans un  membre d’une égalité c’est le remplacer par la valeur   1 .

Procédure permettant de neutraliser un facteur:

Pour neutraliser un facteur il faut et il suffit de multiplier ce facteur par son inverse.

Attention ! ! ! ! pour que l’égalité soit vraie  il faudra multiplier tous les termes  de l’égalité par « cet inverse ».

SUITE DE L’ EXERCICE :

On demandait : Résoudre l’équation    

Après une première transformation nous avions   

Nous avons  dans le premier membre  «  »  ,nous voulons avoir «  »  seul ;il faut donc neutraliser  le facteur «  2 ».

Pour neutraliser le facteur 2 nous multiplierons  le premier membre par l’inverse de 2  (inv 2);

                                     2 fois inv.2   =  2  fois 1/2  (=1)

  ce qui donne pour premier membre :

,mais nous devons multiplier le terme  (ou les termes du deuxième membre par ce même inverse  ;ce qui donne  pour deuxième membre  

nous obtenons la nouvelle égalité :

                       ( )

après calcul      

Vérification:               

soit l’égalité de départ  

le premier membre                           devient 

                                    résultat du calcul  :      donne 

Deuxième membre     17    (dans ce cas il n’y a pas de calcul)

Comparaison du premier membre avec le deuxième membre  17 = 17   

Conclusion:

                         la valeur pour «  »  égale à «  +2.5 »    est solution (et la seule)de l’équation.

Exemples de résolution d’exercices , par la transformation successive d’une égalité .

On se souviendra que ces transformations , sont à l’identique celles que nous sommes obligés de faire lorsque nous cherchons la masse d’une partie d’unobjet ou d’un élément d’un ensemble avec une balance Roberval.

Série 1

 Résultat :  

Résultat :     ou  

Résultat 

TRAVAUX AUTO FORMATIFS.

  ( Ils  peuvent servir de devoir formatif  en tout ou en partie )

CONTROLE :

Pour un devoir il faut  savoir répondre aux questions : Qa ;Qb ;Q1 ; 2 ;3 ;4 ;5

 a) Quel est l’élément neutre de l’addition?

  b) Quel est l’élément neutre de la multiplication?

  c) Dans quel cadre d’action mathématique utilise-t-on la neutralisation?

 d) Dans quel but cherche -t - on  à neutraliser un (ou plusieurs) terme:?

 e) A quoi sert la neutralisation  d’un terme?

1)Lorsque nous  voulons neutraliser un terme  que cherche t - on à faire?

2)Procédure de  neutralisation d’un terme :

a)  Donnez la procédure permettant de neutraliser un terme.

b)  Donnez la procédure permettant de neutraliser un terme dans une égalité.

3)Lorsque nous voulons neutraliser un facteur que cherche t - on à faire?

4) procédure de neutralisation d’un facteur :

a)  Donnez la procédure permettant de neutraliser un facteur

b) Donnez la procédure permettant de neutraliser un facteur dans une égalité .

5)  A quoi est égale la somme d’un terme et de son opposé?

                 (donner son modèle mathématique)

6)A quoi est égale la somme d’un facteur et de son inverse?

        (commentez son utilisation dans le cadre d’une résolution d’équation)

7)A quoi, est égale la somme d’un terme et de son facteur?

8)A quoi est égal le produit d’un terme par son facteur?

9)A quoi est égal le produit d’un terme et de son opposé?

10)A quoi est égal le produit d’un facteur et de son opposé?

EVALUATION :

Série 1