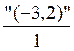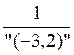|
DOC : formation individualisée soutien en ligne. |
DOC : livre
Elève .Cours interactifs - et
travaux + corrigés. |
|
DOSSIER
N°…….INTERACTIF |
Information « TRAVAUX »
Cliquer sur le mot !. |
|
OBJECTIFS : - Savoir nommer l’opposé d’un nombre relatif ; - Savoir écrire l’opposé d’un nombre (relatif )
ou d’un terme. |
|||
|
|
|
|
Classe de collège 5ème |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
I ) Pré requis:
|
|
|
|
Info 1 :
vocabulaire : lire : les
égalités : partie 1 (code :EGA1) |
|
|
Info 2 : vocabulaire : lire : les égalités : partie 2 (code : EGA2) |
II ) ENVIRONNEMENT du dossier :
|
2.
Les nombres relatifs (vu au
collège) 3.
Prérequis : découvertes sur
les opposés. (vu au collège ) |
1°)Opposé
d’une somme et d’une différence. |
Liste des
cours sur les nombres relatifs. |
OPPOSE d ' un nombre
relatif
Chapitres :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV) INFORMATIONS « formation leçon » :
|
|
Travaux auto -
formation. |
|
|
Corrigé des
travaux auto - formation. |
|||
|
|
|||||||
V ) DEVOIRS
( écrits):
|
Devoir diagnostique L tests. |
|
|
|
|
|
Devoir
Formatif « Contrôle :
savoir » ; ( remédiation) |
|
|
|
|
|
Devoir sommatif . |
|
|
Devoir
certificatif : (
remédiation ) |
|
*
remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour
conclure une formation .
|
Leçon |
Titre |
|
N° |
OPPOSE: (d’un nombre) |
Ne pas confondre « opposé d’un
nombre » et « inverse d’un nombre »
|
Exemples : |
Notation : |
|
Opposé de (-3)
est (+ 3) Opposé de (+3) est
( - 3) |
Opp. (-3) = (+3) Opp. (+3) = ( -3) |
|
Ne pas confondre avec
« inverse » |
|
|
L’inverse de
(-3) est : L’inverse de (+3) est : |
Inv. (-3) = Inv. (+3) = |
|
|
COMMENTAIRE : (cet objectif est à maîtriser pour aborder l
'objectif concernant la transformation des expressions algébriques en sommes
algébriques)
* Ne pas confondre le signe + du
nombre relatif avec le signe opératoire
de l’addition (+) ,pour savoir si le
signe " + " est un signe opératoire ou si le signe " + " appartient à une valeur absolue ,nous devrons savoir si
le nombre est un nombre relatif .( il appartient à l’ensemble des nombres
relatifs).
Exemple : 3
est un nombre entier ¹ ( +3 ) est un nombre entier relatif
Un nombre décimal "non relatif " n’est jamais précédé
d’un signe +;.
En calcul algébrique le résultat est un nombre ; nous devons
toujours obtenir un nombre relatif.
PAR ABUS : Attention : Lorsque nous travaillerons sur les
opérations avec les nombres relatifs
nous devrions transformer les
données dites « simplifiées par
convention » en somme de nombres relatifs:
|
COURS |
|
Transformation de la simplification : |
Retour à l’écriture originelle :
a)
le nombre « 3 » nous
le transformerons en nombre relatif « (+3) » .
b) le nombre « 3 » précédé du signe « -
» ,c’est à dire ( « -3
» ) nous le transformerons
en une addition du nombre relatif
« + (-3) ».
c) si nous avons une suite de
nombre séparés par des signes + ou - ;
par exemples « 3 +
5 » et (3 - 5); nous transformerons l’écriture:
l’addition 3 + 5
deviendra la somme de (+3
) +
( + 5 )
la soustraction 3 -
5 deviendra la somme de
(+3) + (-5)
Se souvenir :
1.)le résultat de l’addition s’appelle
« la somme »
2.l résultat de la soustraction s ’appelle « la différence »
3.le résultat de la multiplication s’appelle « le produit »
4) Terme « algébrique » : on appelle « terme »
une expression formée d’une ou plusieurs lettres , ayant ou non un coefficient
, et qui ne sont séparées par aucun des signes + ou - .
|
II )
Nombres opposés : (dit aussi : nombres symétriques) |
|
+ 4,5
et - 4,5 sont dits opposés . Leur somme
est nulle :
( + 4,5 ) + ( -
4,5 ) = 0
Deux nombres opposés ont la même valeur absolue .
Sur une droite graduée ,
deux points d'abscisses opposées sont symétriques par rapport à l'origine .
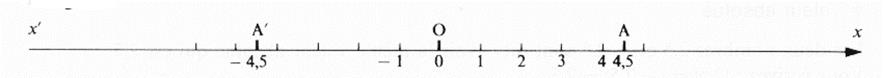
![]() = 4,5 ;
= 4,5 ; ![]() = -4,5
( voir :
mesure algébrique )
= -4,5
( voir :
mesure algébrique )
donc OA = OA' = 4,5 ; O est le milieu du segment [AA'] ou [A'A]
Le point O a pour abscisse 0 .
|
|
|
commentaire: en algèbre , on utilisera l’opposé du nombre relatif (ou d’un terme) pour neutraliser un terme dans un membre d’un
égalité ; ou pour transformer une soustraction de deux nombres relatifs en
« addition » .
a) Notation: La notation mathématique de « opposé »
d’un nombre « a » est : opp. a
b) Procédure :
Pour obtenir l ’ opposé d’un nombre relatif (ou terme) il suffit de changer le signe ( +
par - ou – par + )du nombre relatif ou le signe ( + par - ou
– par + )contenu dans le terme.
c) Résultats:
L’opposé
de (+3 ) se notera
« opp. (+3) »,on dira que l’opposé de +3 est -3,ce qui se traduira en écriture
mathématique:

opp. (+
3) =
( - 3)
L’opposé de
(- 3) se notera « opp. (-3 ) » ,on dira que l’opposé de
(- 3) est (+3) ,
ce qui se
traduira en langage mathématique:
opp. (- 3) =
L’opposé du terme 3x se notera « opp. +3x » ,on dira que l’opposé de
3x est -3x
,ce qui se traduira par: opp. 3x
= -3x
Exemples: opp. +3/5 = -
3/5
opp. -7 est
égal à +7
généralisation : opp. (+ a) = (
- a )
|
IV
) Représentation graphique d’un nombre et de son opposé: |
|
Pour donner la représentation graphique de
l’opposé d’un nombre est un point .Il faut tracer une droite graduée (celle
représentant les nombres relatifs ) dont le centre aura pour valeur « 0 »
pt. A’ pt.A
![]()
(-x)
(x )
(- 3) 0 (+ 3)
*On peut dire qu’un nombre et son opposé
sont symétriques par rapport au
point « 0 »,on dit
aussi « symétrie centrale »,(par rapport au centre « 0 »
).
Remarques : l’opposé de « 0 » est
« 0 ».
Procédure : Pour obtenir l’inverse d’un nombre il
faut construire une fraction de numérateur égal à 1 et de dénominateur
égal à ce nombre ;
Procédure permettant d’obtenir l’inverse d’un nombre:
|
|
Exemples numériques |
|
1) mettre le nombre sous forme de fraction de
dénominateur égal à 1 : "a" = |
"3" = "3,2" = "(-3,2)" = |
|
2)Inverser les "termes" de la
"fraction": mettre le numérateur en dénominateur ; et mettre le
dénominateur au numérateur |
3" = "3,2" = "(-3,2)" = |
|
3)Rendre compte |
Inv. 3" = Inv. "3,2" = Inv. "(-3,2)" = |
|
Leçon |
Titre |
|
N°2 rappel |
TRAVAUX d ’ AUTO - FORMATION sur OPPOSE: (d’un nombre) |
TRAVAUX N°2 d ’ AUTO - FORMATION : CONTROLE
1)Donner un
modèle d’écriture mathématique de
« opposé d’un nombre »
2)A quoi va
servir l’opposé d’un nombre?
3)Traduire en
langage mathématique: opposé d’un
nombre « a » .
4)Donner la
procédure permettant d’obtenir l’opposé d’un nombre.
5)Traduire en
langage littéral:
a )
opp. a :...........................................
b )
opp . -a :...........................................
TRAVAUX N°2
d ‘ AUTO - FORMATION EVALUATION
I) Faire les
exercices suivants :
opp. (-5 )
=...................
opp (+ 4
) =..................
opp. (+ 3 / 4
)= ................
II) Faire les exercices suivants:
opp. x =
opp 1 /x =
INTERDISCIPLINARITE:
1°)Symétrie centrale
d’un point dans un repère : ( INFO
PLUS ? ? ? ?)
Si A ( +3 ; +2) ; son image ( B) dans la symétrie
centrale est
B (
opp.+3 ; opp.+2)
Soit B ( -3 ; - 2)
2°) Pour une banque :
« l’ opposé de 50F » signifie
: « débit de 50 F» ; 50 F
est la somme que vous retirez de votre compte.
Lecture d'un relevé de banque:
Le relevé de banque comporte deux colonnes :
La colonne des nombres intitulée : débiteur
Cette colonne
indique les nombres correspondant au montant des sommes d'argent que vous avez
"dépensée" :cheques , carte bleue ; mensualité de crédit
……(nombres négatifs)
La colonne des nombres intitulée : créditeur
Cette colonne
indique les nombres correspondant au montant des sommes d'argent que vous avez
"reçu" : salaire ; prime ; indemnités ….
(nombres
positifs)
|
|
DEVOIR formatif : |
|
CONTROLE:
OPPOSE: (d’un nombre)
1°) Traduire
en langage mathématique: opposé d’un
nombre « a » .
2° ) Donner
la procédure permettant d’obtenir
l’opposé d’un nombre.
EVALUATION :
I) Faire les exercices
suivants :
opp. (-7,5 )
=...................
opp. (+ 4 ,7
) =..................
opp. (- 3 / 4 )= ................
II) Faire les
exercices suivants: ( transformer l’ écriture)
opp. x =
opp 1 /x =