|
DOC : formation individualisée soutien en ligne. |
DOC : livre Elève .Cours interactifs - et travaux + corrigés. |
Dossier 2 / 5
: LES EGALITES (2/5)
(nomenclature) : les membres d’une égalité
|
DOSSIER N°4-B :INTERACTIF |
Information « TRAVAUX »Cliquer sur le mot !. |
|
OBJECTIFS :- Savoir reconnaître les membres
d’une égalité . |
I ) Pré requis:
|
|
II ) ENVIRONNEMENT du dossier :
|
Objectif précédent : |
Retour vers les activités avec les
N. |
||
|
1°)Algèbre ; les égalités ;
les éléments neutres ; neutralisation d’un terme
et d’un facteur. |
III ) LECON n° 4-B : Dossier 2 / 5 :
LES EGALITES
(2/5) (nomenclature) : les membres d’une égalité
Chapitres
:
|
¥ |
|
|
¥ |
|
|
¥ |
IV) INFORMATIONS
« formation leçon » :
|
Interdisciplinarité |
|
||||||
|
|
Corrigé des travaux auto - formation. |
||||||
|
|
|||||||
|
Devoir diagnostique L tests. |
|
|
|
|
|
Devoir
Formatif « Contrôle :
savoir » ; ( remédiation) |
|
|
|
|
|
Devoir sommatif . |
|
|
Devoir certificatif : ( remédiation ) |
|
* remédiation : ces documents peuvent être réutilisés ( tout ou partie) pour conclure une formation .
|
Leçon |
Titre |
|
N°2/5 |
LES EGALITES (2/4) (nomenclature) : Définition :
les membres d’une égalité |
CHAPITRES
|
¥ |
|
|
¥ |
|
|
¥ |
Commentaire :
dans la première leçon ( 1/4 ) nous avons
« disséqué » une expression algébrique ; dans la leçon 2 / 4 ;
nous avons deux expressions algébriques que nous séparons par un signe « = » . Nous allons nommer les éléments de cette
égalité !
, ces « mots » seront toujours utilisés en algèbre
.
Définition
de l’objectif :savoir
reconnaître une égalité ,et les « membres » de cette égalité.
|
|
Rappel : Le signe de l’égalité: |
|
Le
signe de reconnaissance de l’égalité est
le symbole : «
= »
Ce qui suit est incontestable : Dans une égalité
, ce qu’il y a « à droite » du signe « = » est égale
à ce qu’il y a « à gauche » du signe égal ( = ) .
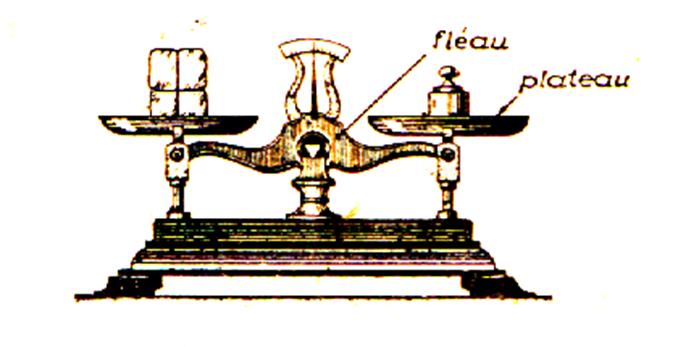
Penser à prendre en exemple la
balance de Roberval : il y a autant à gauche qu’à droite ;
la justice est aussi symbolisée avec une balance ..
|
Balance ROBERVAL : les
plateaux sont horizontaux , l’aiguille réglée au
zéro. |
|
construction
de ce symbole: deux traits forts ,parallèles ,et
parallèle a la ligne d’écriture, d’environ 3 mm de longueur.
C’est le signe le plus utilisé. !
Quand
ce n’est pas égal : on dit « inégal » le symbole est :¹
|
|
|
Les écritures mathématiques ( appelées aussi « expressions algébriques » )
situées à gauche et à droite du signe
« égal » s’appelle des membres.
Un
membre est souvent une expression algébrique, qu ‘il faut transformer.
Premier membre: La
partie située à gauche du
signe « égal » s’appelle « premier membre ».
Deuxième membre: La partie située à droite du
signe « égal » s’appelle
« deuxième membre »
*A savoir : Dans une égalité
il n ’
y a que deux membres .
Ce que peut
« contenir » un membre :
dans une égalité un membre
peut :
= valoir
zéro (..........= 0 )
=contenir un terme
(de un ou plusieurs facteurs) ,on dira « monôme »
......................=
7 ; ...................... = 3x ; .......................= 2ab
=être un
somme de termes si il y a deux termes on
dira « binôme »
= être un somme
de termes si il y a trois termes on dira
« trinôme »
= si il y en a plusieurs
termes (deux ou plus ) ,dans ce cas , ce membre
pourra prendre le nom de
« polynôme »
exemple : .................. =
3 -5.2 x +12 (est un polynôme)
|
|
|
On donne une égalité ;il faut
identifier et nommer tous les symboles qui constituent cette égalité . (par
convention : on lit toujours de
gauche à droite)
Pour l ’ égalité de deux polynômes notés
« A » et
« B » ;on écrira:
A =
B
Si « A » est composé de (contient) plusieurs « monômes »
ou « termes »
: « a - b c + g »
et
si « B » est égal
à « e d
- f / a + x² »
On
écrira:
a - b
c +
g = e d
- f / a + x²
on nommera :
1°
membre = 2° membre
Commentaires sur : « ce que l’on peut dire »
sur ces écrits , on pourra énoncer que :
Dans l’égalité : a - b
c + g =
e d - f / a + x²
* On
transformera chaque membre en somme algébrique afin d’
identifier tous les termes .
a - b
c +g se transforme en somme algébrique : (+a) + ( - b c) +
( +g)
e
d - f / a +
x² se transforme en somme
algébrique : ( +e d ) + ( - f / a ) + ( +
x² )
* Ainsi : (+a) ; ( - b
c) ; ( +g) ; ( +e d ) ; (
- f / a ) ; ( + x² ) sont les termes de l’égalité
si l’on simplifie les écritures ,on dira
que « a » ;
« -b c » ; « g » ; « e d » ; « -f / a » ;
« x² » sont
aussi les termes de l’égalité ;
On pourra dire que :
* « a
» est le premier terme du premier membre
* « -b
c » est le deuxième terme du
premier membre.
* « g » est
le troisième terme du premier membre.
* « e d » est le premier
terme du deuxième membre ( on peut dire aussi le quatrième terme de l’égalité.
* « -
f / a » est le deuxième terme du deuxième membre ( ou le cinquième terme de l’égalité);
* « x² » est le troisième terme du
deuxième membre de l’égalité (ou le sixième terme de l’égalité)
Il peut être écrit des choses complémentaires
, cette liste n’est pas exhaustive .
Les
facteurs du premier membre sont : a ; -b ; c ;g ;
les
facteurs du deuxième membre sont : e ; d ;-f ;
1 /a ; x1 ; x2
|
Leçon |
Titre |
|
N°4-B |
TRAVAUX d ’ AUTO - FORMATION sur : LES EGALITES (2/4)
EG2 (nomenclature) |
TRAVAUX N°4-B
d ’ AUTO - FORMATION : CONTROLE
1. Comment
reconnaît - on une égalité?
2. Donner les caractéristiques du symbole de l’égalité.
3. Combien y a-t-il de membres dans une égalité?
4. Comment appelle-t-on la partie à droite du signe « égal
»?
5. Comment appelle-t-on la partie à gauche du signe « égal » ?
6. Comment appelle-t-on un seul terme ?
7. Comment appelle-t-on deux
termes?
8. Comment appelle-t-on plusieurs
termes?
9. De quoi peut être constitué un
membre ?
10. Qu’est ce qu’un « monôme »?
11. Qu’est ce qu’un
« Binôme »?,
12. Qu’est ce qu’un polynôme ?
13. Qu’est ce qu’un trinôme ?
14. Qu’appelle-t-on
« premier membre » ?
15. Qu’appelle-t-on « deuxième membre » ?
TRAVAUX
N°4-B d ‘ AUTO - FORMATION EVALUATION
1°)
B contient « a -e d + f »
2°) A
contient « c b - g / t »
Dites ce que l’on doit savoir sur l’égalité : B
= A