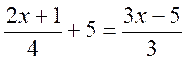Les égalités   « résoudre »

cliquez ici

Les éléments et ensembles

cliquer ici

Index  warmaths

Objectif précédent :

1°) Tout sur les égalités (vocabulaire …)

2°)  Neutraliser un terme et un facteur ; et « résoudre »  

3°) Les théorèmes sur les transformation d’ égalités.

Objectif suivant :

1°) Algèbre  les conventions d’écritures.

2°) Equation du premier degré à 1 inconnue.

Tableau    12info

Définition de l’Objectif:

   Connaître  et utiliser les quatre théorèmes de l’égalité.

TEST

COURS

Devoir  Contrôle

Devoir évaluation

2°) exercices « résoudre »

Interdisciplinarité

1°) Transformations de formules

Corrigé Contrôle 

Corrigé évaluation 

Les transformations d’égalités simples utilisées en mathématique et sciences

Les égalités et les sciences ; en lien avec les cours et problèmes  

En résumé ( à retenir )  : 

THEOREME 1 : On obtient une équation équivalente à une équation donnée en ajoutant à ses deux membres une même expression algébrique.

         THEOREME 2:  On obtient une équation équivalente à une équation donnée en multipliant ou en divisant les deux membres  par un même nombre DIFFERENT DE ZERO.

COURS

Rappel : Résoudre une équation c’est trouver ses solutions.

On dit que deux équations sont équivalentes lorsqu’elles admettent les mêmes solutions.

Pour résoudre une équation, on la transforme en équations équivalentes jusqu’à ce qu’on obtienne une équation dont la résolution est immédiate. Pour cela, on utilise certains théorèmes que nous allons démontrer.

 Sot une équation  (1)     A = B

Et l’équation (2)  A + C = B + C obtenue en ajoutant une même expression algébrique « C » aux deux membres de l’équation (1).

1°) soit « x » = a une solution de l’équation (1). Dire que « a »  est solution de l’équation(1) c’est dire que les valeurs A’ et B’ que prennent A et B lorsqu’on remplace x par a sont égales.

  A’  = B ‘

 Pour x = a , C prend une valeur C’ . Puisque A’  =  B’ on a    A’ + C’ = B’ + C’

Or A’ + C’ et B’ + C’ sont les valeurs que prennent les deux membres de l’équation (2) lorsqu’on remplace x par a .Ces deux valeurs sont égales ; cel  a prouve que a  est racine de l’équation (2).

2°) On démontrera de la même façon que toute racine de l’équation (2) est racine de l’équation (1) (qu’on peut considérer comme déduite de (2) en ajoutant aux deux membres la même expression -C)

Donc les équations (1) et (2) sont équivalentes, c’est à dire :

On retiendra :

THEOREME 1 : On obtient une équation équivalente à une équation donnée en ajoutant à ses deux membres une même expression algébrique.

Remarque I : la démonstration précédente suppose qu’on peut calculer la valeur C’ de C pour x = a . En particulier, il en sera toujours ainsi si C est un polynôme.

  Remarque II : Nous avons fait la démonstration précédente en supposant qu’il s’agissait d’une équation à une inconnue. On raisonnerait de la même façon pour une équation à plusieurs inconnues et on serait conduit au même résultat.

COROLLAIRE.  Soit l’équation :

(1)  2 x + 5 = 5x -7

Ajoutons aux deux membres d’expression « -2x » .On obtient l’équation équivalente :

(2)  5 = 5x -7x -2x

Ces deux équations ne diffèrent que par le terme « 2x » qui , dans l’équation(1), est dans le premier membre précédé du signe + et, dans l’équation (2), dans le second membre précédé du signe - .Donc :

On obtient une équation équivalente à une équation donnée en faisant passer un terme d’un membre dans l’autre et en changeant son signe.

THEOREME II.

Soit l’équation

(1)   A = B

Et l’équation (2)      mA = mB   obtenue en  multipliant les deux membres de l’équation ( 1)  par un même nombre « m ».

Ces deux équations sont respectivement équivalentes à :

                      A - B  = 0

Et à      m A - mB = 0

C’est à dire   m ( A - B) = 0

1°) Toute solution de l’équation (1)  annule  A- B donc annule le produit  m(A-B), par suite est solution de l’équation (2)

2°)  Toute solution de l’équation (2) annule le produit  m(A  -B), donc annule  A - B ou m .

On pourra affirmer qu’elle annule  A-B , ‘est à dire est solution de l’équation (1) si m est différent de zéro.

Donc si m ¹ 0 les équations (1) et (2) sont équivalentes.

D’autre part , comme on passe de l’équation (2) à l’équation (1) en divisant les deux membres par m, on est conduit à l’énoncé suivant :

On retiendra :

THEOREME 2: On obtient une équation équivalente à une équation donnée en multipliant ou en divisant les deux membres  par un même nombre DIFFERENT DE ZERO.

Cas particulier : On  peut changer les signes des deux membres d’une équation. Cela revient en effet à multiplier les deux membres par -1

APPLICATION :

Soit l’équation :     

Multiplions les deux membres par 12  . On obtient  l’équation  équivalente :

  3 ( 2x +1) + 60 =  4 (3x -5)

dans laquelle les deux membres n’ont pas de dénominateur.

         On dit qu’on a chassé les dénominateurs.

En résumé :  on retiendra ::::

THEOREME 1 :               On obtient une équation équivalente à une équation donnée en ajoutant à ses deux membres une même expression algébrique.

         THEOREME 2:                     On obtient une équation équivalente à une équation donnée en multipliant ou en divisant les deux membres  par un même nombre DIFFERENT DE ZERO.

Devoir sur  les transformations de formules