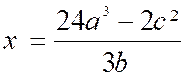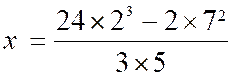II est difficile, dès le principe, de définir l'algèbre d'une manière intelligible ; néanmoins nous allons essayer d'en faire comprendre le but par les considéra­tions qui suivent.

Dans toutes les questions que l'on peut se proposer sur les nombres, il existe des quantités connues qu'on appelle les données de la question, et des quantités in­connues qu'il s'agit de déterminer. L'arithmétique nous a appris, en général, par quelle série d'opérations et de raisonnements on arrive à la détermination des incon­nues ; mais les calculs successifs qu'on effectue sur les nombres modifient les quantités connues, de telle sorte qu'on ne voit plus? les relations qui lient ces données au résultat final. Aussi, pour chaque question du même genre, faut-il recommencer et le raisonnement et les opérations.

L'algèbre, au contraire, à l'aide de certains signes, permet de généraliser les résultats et d'en déduire des règles applicables à toutes les questions qui diffèrent seulement entre elles par les données numériques. C'est ce que nous allons éclaircir par quelques exemples.

"premier exemple :

. On demande la somme des trois nombres 3, 4 et 5.

La solution du problème est évidemment 12 ; mais ce résultat n'emporte pas avec lui la trace des nombres qui l'ont donnée ni de l'opération effectuée, en sorte qu'on ne sait plus si 12 est la somme des trois nombres 3, 4 et  5 , ou de deux autres nombres tels que 7 et 5, plutôt que le produit de 3 par 4, ou de toute autre combinaison.

Mais si, au lieu d'effectuer l'addition, on se contentait de l'indiquer par le signe  +  en posant 3 +  4 + 5, ce procédé aurait l'avantage, non seulement de présenter le résultat 12, mais encore de laisser en évidence les nombres et l'opération qui l'ont fourni, On voit déjà combien l'introduction d'un signe algébrique est importante

Deuxième exemple. :

 On demande quel est l'intérêt à 5 % 'de 2348 €  . pour 56 jours (*).

On dira :

puisque 100 €  . produisent 5  €  d'intérêt dans un an ou 360 jours (année commerciale), un euro rapportera     ; donc 23 48 euros . rapporteront 

c'est-à-dire 117 euros . 40 c.

Si l'on divise maintenant cette dernière somme par 360, ou aura, pour l'intérêt  d’un jour  du capital proposé

 € ;  ce nombre, multiplié par 86, donnera enfin pour l'in­térêt demandé

.

Tel est le résultat que nous fournit l'arithmétique ; mais rien ne fait voir comment ce résultat final est lié aux données du problème ; de sorte que si l'on changeait dans l'énoncé le capital, le taux, le temps, il fau­drait, pour trouver la solution, reprendre la même série  de raisonnements et de calculs.

Voyons comment on traiterait cette question en algèbre

On représenterait le capital par la lettre c, le taux par t  et le nombre de jours par n.

Ces lettres ont l'avantage de représenter indifféremment un capital, un taux, un temps quelconques. Cela posé, on dirait :

Si le  capital 100 € . produit en un an un intérêt marqué par t, un  euro  de capital produira seulement     et le capital c   donnera un intérêt annuel de   

mais pour un seul jour l'intérêt n'est que la 360^ème  partie de cette dernière expression, c'est-à-dire      

donc enfin l'intérêt du capital c   pour un nombre quel­conque de jours n  sera exprimé par 

On voit par là qu'en général on obtient l'intérêt d'une somme en multipliant le capital par le taux et par le nombre de jours, et en divisant le produit par 36000,

Cette expression finale prend le nom de formule. Une formule est donc un tableau indiquant les opérations à effectuer sur les données d'un problème pour trouver la valeur de l'inconnue

Or, dans toutes les questions qui traitent des nom­bres et des grandeurs en général, l'algèbre a pour but d'obtenir des formules qui s'appliquent à toutes tes questions de même espèce; on pourrait donc définir l'algèbre : la science des formules mathématiques.

La discussion des formules conduit à la détermination de certaines lois que l'arithmétique est impuissante à découvrir.^

II ) Des signes algébriques. :

1                       )   Lettres.

On a compris, par le dernier exemple ci-dessus, l'avantage de substituer des lettres aux données numériques d'un problème; aussi est-il d'usage, en algèbre, de représenter les nombres connus par les premières lettres de l'alphabet a, b, c, etc. , et les inconnus par les dernières lettres x, y, z.

2        ) Signes.

On conçoit que, pour soumettre les lettres au calcul, il y aura nécessité de faire usage de certains signes. Nous connaissons déjà ceux dés quatre opéra­tions fondamentales, et nous savons que a + b   in­dique l'addition des deux quantités  a et b,  a — b   leur soustraction,  a X b leur produit, et  ou  a :  b   leur quotient.

Observons seulement que l'on se dispense ordinaire­ment de mettre entre les facteurs le signe de la multiplication X, et qu'on se contente d'écrire ab au lieu  de a X b et mnp pour m X n X p. Cette simplification ne peut s'appliquer à des facteurs numériques  3x4,  parce que la suppression du signe donnerait 34.

Quelquefois on indique aussi la multiplication par un point placé entre les facteurs; ainsi, a.b est la même chose que a X b ou que ab; de même 3.4 dé­signe le produit 12 de 3 par 4.

On indique l'égalité de deux quantités par le signe = ; ainsi, l'on écrit a = b   pour exprimer que la valeur numérique de a est égale à celle de b.

Pour marquer l'inégalité on se sert des signes  > , < ; ainsi, a > b signifie et s'énonce a plus grand que b ; m < n indique que m est plus petit que n.

3) Coefficient. Quand une quantité doit être ajoutée plusieurs fois à elle-même, on abrège l'écriture de la manière suivante : au lieu de a + a +  a, on écrit 3a ; de même', au lieu de bc bc, on écrit 2bc . Le nombre placé devant une ou plusieurs lettres devient un facteur et prend le nom de coefficient.

Le coefficient peut être fractionnaire, comme dans l'expression  a    qui signifie   ou bien

5. Exposant. Lorsqu'une lettre entre plusieurs fois comme facteur dans un produit, on l'indique par un nombre placé à droite de cette lettre et un peu en haut ; ainsi, au lieu de aaa, on écrit a³ : ce nombre « 3 » s'appelle exposant. On écrira pareillement a⁷, b ³  pour marquer la 7^ème  puissance de a et la 3^ème  puis­sance de b.

         On doit bien éviter de confondre le coefficient avec l'exposant, et se rappeler pour cela que le coefficient se place avant  la lettre sur la même ligne, tandis que l'ex­posant s'écrit après la lettre, au-dessus et en petit ca­ractère. Ainsi les expressions 3a  et a³ ont une signification bien différente; car, en supposant a = 6, on aura 3a = 3 X 6 = 18, tandis que a ³ = 6 X 6 x 6 = 216.

Une lettre écrite seule est considérée comme ayant l'unité pour coefficient et pour exposant ; ainsi a équi­vaut à   l a¹.

6 - . signe radical. Enfin, pour indiquer l'extraction des racines, on fait usage du signe      qu'on appelle radical, et l'on place sur l'ouverture le nombre qui marque le degré de la racine à extraire; ainsi  ,   expriment la racine cubique et la racine cinquième de la quantité   a. .   Ce nombre s'appelle l'indice de la racine.

Pour indiquer l'extraction, de la racine carrée, on se dispense d'affecter le radical de l'indice ²  , (  ) , et l'on écrit seulement .

III ) Dénominations algébriques

Pour terminer ces notions préliminaires, il nous reste encore à définir certaines expressions fréquem­ment employées en algèbre.

Nous sommes dans le cas ou les sommes algébriques sont transformées ( après simplification) en expression algébrique.

1°) Quantité littérale.

 On appelle en général quan­tité littérale ou quantité algébrique toute quantité ex­primée par des lettres telles que 7 ab ;  3a — b ; 5  a³...

2°)  Terme.

On donne le nom de terme  à  toute quan­tité algébrique précédée du signe +  ou du signe —.

Le terme est dit positif quand le signe +   le précède, et négatif  lorsque c'est le signe — ; ainsi +  60a² ;  + a² b sont des termes positifs, tandis que les termes — 5 b ;  — am³ sont négatifs.

     Tout terme écrit sans aucun signe est censé avoir le signe +  ; ainsi 4ab² est la même chose que le terme positif +  4ab ² 

       Le signe + ou — fait partie intégrante du terme.

Nous sommes dans le cas ou les sommes algébriques sont transformées ( après simplification) en expression algébrique., dans la somme algébrique les termes sont séparés par le signe opératoire + ..

3°)  Monôme. On appelle monôme une expression algébrique qui n'a qu'un seul terme, telle que   - 5 a ; ou  ; ou bien ¾ a²b

4°)  Polynôme. On donne le nom de polynôme en  général à toute expression ou quantité algébrique com­posée de plusieurs termes, et l'on appelle en 'particulier binôme la réunion de deux termes, trinôme celle de trois termes ; ainsi a  + b et    sont des binômes, et 5a² - bc + b^S est un trinôme.

5°) Termes semblables .

Dans un polynôme il peut se rencontrer des termes semblables ; on appelle ainsi les termes composés des mêmes lettres affectées des mêmes exposants, quels que soient d'ailleurs leur signe et leur coefficient; par exemple:   5a²b ; -   a²b  et  7 a²b sont trois termes semblables ; de même 20 a³ b² x  et — 12 a³ b² x ; 8 a³ b² x  sont semblables.

Valeur numérique.

Dans les expressions littérales  les lettres représentent des valeurs quelconques ; mais ces valeurs sont déterminées dans chaque cas par­ticulier, de manière que si l'on remplace chaque lettre par sa valeur et qu'on effectue tous les calculs indiqués, l'expression algébrique sera traduite en un  nombre, lequel est la valeur numérique de cette expression. Cette valeur numérique sera, selon le cas, entière ou fractionnaire, positive ou négative.

Par exemple, supposons que dans l'expression 4a² b on fasse a = 9 et 6 = 2. La substitution de ces valeurs particulières donnera :

4 x9² x2 = 4x81x2 = 648,

et l'on dira que 648 est la valeur numérique de l'expression  4a²b  pour le. cas déterminé

Soit encore l'expression : 

Si l'on suppose a = 2,  b = S,  c — 7, la formule  devient       

ce qui donne, en effectuant les calculs,

 ; donc la valeur de l'inconnue x est dans ce cas 6 unités 4 quinzièmes.