Pré requis:
|
|
|
|
SCIENCES : le système métrique |
|
Objectif
précédent : Information complémentaire : |
Objectif suivant
"N"
1°)
la division euclidienne |
2°) Liste
des cours sur les puissances et les racines. |
|
|
Ou « Puissance d’un nombre relatif» ou |
|||
|
|
|
|
|
DOSSIER « Puissances
et racines »:
PUISSANCE
(partie 1/5 ) :
appliquée aux Nombres entiers et décimaux dit
"positifs"
Partie 1 : Puissance d'un nombre entier (dans N):
- Définition ;
- Le carré d’un
nombre ; table de Pythagore.(le carré parfait )
- Le cube d’un
nombre ( N )L le cube parfait)
PARTIE 2 : PUISSANCES
"carré" et "cubique"
dans l'ensemble des nombres décimaux
(D) :
- Le "carré
" d'un nombre décimal ( D ) :
- Le "cube
" d'un nombre décimal ( D ) :
|
COURS
|
Interdisciplinarité 1°) application aux
sciences |
|
|||||
|
|
|
|
|
|
|||
Partie
1 :
Puissance d'un nombre entier (dans
N):
A) DEFINITION:
On appelle
"puissance d'un nombre" , la multiplication d ' un nombre par lui
même.("n" fois par lui même)
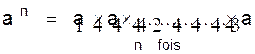
B ) Le CARRE D' UN NOMBRE ( N ): (info
plus : un nombre au carré , ou
l’aire d’un carré )
a)Définition
:
On appelle
"carré d'un nombre" , le résultat de la
multiplication d ' un nombre par lui même.(exemple de
multiplication 3![]() 3 ) .
3 ) .
On dit aussi : On
appelle "carré d'un nombre" ,
le produit d ' un nombre par lui même.
b)
Convention d ‘écriture :
|
|
rappel :sur un
l’exposant. |
On remplacera
l'écriture "3![]() 3 " par l'écriture : 3 2
3 " par l'écriture : 3 2
le "deux " : se dit : "au carré " ; " à la puissance 2" ;"exposant 2"
ainsi
on peut traduire 3 2 suivant les trois expressions :
3 2 remplace
la multiplication 3![]() 3 ; on peut dire
" trois au carré" ; et se note 3 2
3 ; on peut dire
" trois au carré" ; et se note 3 2
3 2 remplace la multiplication 3![]() 3 ; on peut
dire "trois à la puissance
deux" se note 32
3 ; on peut
dire "trois à la puissance
deux" se note 32
3 2 remplace la multiplication 3![]() 3 ;
on peut dire "trois exposant
deux" et se note 32
3 ;
on peut dire "trois exposant
deux" et se note 32
Conclusion: 3![]() 3 s ' écrira , sous forme simplifiée
, 32 ,on pourra dire : trois au carré ; trois à la puissance deux ou
trois exposant deux .
3 s ' écrira , sous forme simplifiée
, 32 ,on pourra dire : trois au carré ; trois à la puissance deux ou
trois exposant deux .
Observons
la table de Pythagore :
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
|
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
|
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
|
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
|
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
|
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
|
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
Le produit d’un nombre
entier par lui- même donne un résultat particulier ,
on leur attribue un nom particulier : « produit parfait » ou « carré parfait » ( « carré » à
mettre en relation avec le calcul de l’aire du carré)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
La multiplication
d ' un nombre entier naturel par lui
même s'appelle "carré parfait :
On dit aussi : Si "a" est un nombre entier ; la multiplication d ' un nombre par lui même s'
appelle "carré parfait":
exemple 3 ![]() 3 s ' écrit 3 2
3 s ' écrit 3 2
On dit encore : Le
carré des nombres entiers s' appellent "carrés parfaits"
les dix premiers carrés parfaits
sont :
|
12 |
22 |
32 |
42 |
52 |
62 |
72 |
82 |
92 |
102 |
|
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
1 ;4 ; 9 ; 16 ;25 ;36 ;49
;64 ;81 ; 100 (voir les tables de
multiplication : il y a un carré parfait par table )
pour le calcul
mental ; il faudra savoir les
carrés parfaits des nombres de 1 à 13 , et des dizaines ( 102 ;
…. ; 902 ;) et des centaines (1002 ; …. ; 9002 ;
..)
Ces calculs sont à la base des calculs
« mental » avec. Les I.R.( utiliser pour le calcul mental des carrés de certain
nombres entiers tel que : 212 ; 222 ; 392 ;
412 ; …….. ; et les
multiplications tel que 47 ![]() 53 ;
53 ;
|
Pour en savoir plus ( carré ou puissance 2) |
C ) Le CUBE
D' UN NOMBRE ( N ):
a
)
Définition : On appelle "cube" d'un nombre la multiplication d ' un nombre par lui même ; par lui même : (a![]() a
a ![]() a)
a)
La multiplication " 5 ![]() 5
5 ![]() 5 " sera
remplacée par l'écriture :
5 3
5 " sera
remplacée par l'écriture :
5 3
le nombre "trois " : en haut
à droite d’un nombre (ou lettre) se dit
: "au cube" ; " à
la puissance 3"
;"exposant 3"
ainsi
on peut donner trois expressions à :
5 3 remplacera l'écriture 5![]() 5
5 ![]() 5 ; on dira : « cinq au
cube »
5 ; on dira : « cinq au
cube »
5 3 remplacera l'écriture 5![]() 5
5 ![]() 5 ;
on pourra dire « cinq à la puissance trois »
5 ;
on pourra dire « cinq à la puissance trois »
5 3 remplacera l'écriture 5![]() 5
5 ![]() 5 ; et on dira encore « cinq exposant
trois »
5 ; et on dira encore « cinq exposant
trois »
résultat du
calcul de 5 3 = 125
c ) Calculs
:
|
Dans
N |
|
|
4 |
= 64 |
|
23 = |
= 8 |
|
5 |
= 125 |
d )Le "CUBE
PARFAIT"
On appelle : "Cube
parfait" la multiplication d'un
nombre entier naturel par lui même ;
puis par lui même.
Autrement dit : Le
« cube » d’un nombre est le
produit de trois facteurs égaux à ce nombre
Autre façon de dire :
Si "a" est un nombre
entier ; la multiplication d ' un nombre
par lui même par lui même s' appelle "cube parfait":
On dira encore : Le cube des nombres entiers s' appellent
"cubes parfaits"
les dix premiers cubes
parfaits sont : 1 ;8 ; 27 ; 64; 1000
|
13 |
23 |
33 |
43 |
53 |
63 |
73 |
83 |
93 |
103 |
|
1 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
729 |
1000 |
|
Pour en savoir plus sur le "cube ou
puissance 3" |
PARTIE 2 :
PUISSANCES "carré" et "cubique" dans l'ensemble des nombres décimaux (D)
a) Le
"carré " d'un nombre décimal ( D ) :
exemple: 3,2 2
Tout nombre multiplié par lui même , s'appelle
: "carré" de ce nombre.
Exemples :
|
Dans D |
|
|
2,1 |
2,1 2 =
4,41 |
|
4,3 |
4,32 = 18,49 |
|
5,7 |
5,72 =
32,49 |
|
352,4 |
352,42 =
124185,76 |
b)
Le "cube " d'un nombre décimal (D ):
Tout nombre multiplié
par lui même , et multiplié ,à nouveau
par lui même , s'appelle :
"cube" de ce nombre.
Exemple : 3,2 ![]() 3,2
3,2 ![]() 3,2 s’écrit
3,2 3
3,2 s’écrit
3,2 3
Exemples :
|
Dans D |
|
|
2,1 3 =
9,261 |
|
|
3,2 |
3,2 3 =32,768 |
|
4,3 |
4,3 3 =79,207 |
|
5,7 |
5,7 3 = 185,193 |
|
352,4 |
352,43 =
43763062 ? |
INTERDISCIPLINARITE:
APPLICATION à
l' ALGEBRE: simplification
d'écriture
|
L'écriture |
Devient l'écriture |
|
xxx |
x3 |
|
m |
m3 |
|
(dm) |
(dm)3 |
|
(cm) |
(cm)3 |
|
(mm) |
(mm)3 |
|
I |
I3 |
|
(AB) |
(AB)3 |
Travaux auto formatifs :
1 °)Qu'appelle - t- on "puissance d '
un nombre" ?
2°) Comment appelle- t -
on le nombre indiquant la puissance d'un nombre ? (SOS cours)
3°)
Qu'est ce qu'un carré parfait ?
4°) Qu'est ce qu'un cube parfait ?
5° )Que signifie "carré d'un
nombre" ?
6° )Que signifie " cube d'un
nombre" ?
7°) Traduire en langage littéral
de trois façon : (3)2
8°) Pourquoi (-5) (+5) n 'est pas égal à
(+5)2 ou (-5)2 ?
9°) Traduire en langage littéral de trois
façon : (-3)3
10°) Pourquoi (-5) (+5) (-5) n 'est pas égal à
(+5)3 ou (-5)3 ?
le
carré:
Ecrire de façon
simplifiée :
2![]() 2 : …=……
2 : …=……
xx
= …… ….
m![]() m … ..=……
m … ..=……
dm![]() dm =……
…..
dm =……
…..
cm![]() cm =……
…..
cm =……
…..
mm![]() mm =……..
mm =……..
Traduire en écriture
numérique :
deux au carré :……… ………..
deux à la puissance deux :………… ………
deux exposant deux :……………
Que signifie :
"carré parfait" ?……
Citer les 13 premiers carrés parfaits:………….
"cube"
:
Ecrire de façon
simplifiée :
2![]() 2
2 ![]() 2 : ……………….
2 : ……………….
xxx :…………
m![]() m
m ![]() m……………..=…
m……………..=…
dm![]() dm
dm ![]() dm
=…… …..
dm
=…… …..
cm![]() cm
cm ![]() cm
=…… …..
cm
=…… …..
mm![]() mm
mm ![]() mm
=… …..
mm
=… …..
Traduire en écriture
numérique :
deux au cube :…… ………..
deux à la puissance trois :……… …………
deux exposant trois :…………… ………
Citer les 5 premiers
cubes parfaits ( plus deux autres nombres
):………….
1 ) Donner un carré
parfait (de 6 chiffres ) ; justifier
votre résultat !
2 ) Donner un cube parfait (de
6 chiffres ) ; justifier votre résultat !
3 ) Citer les dix
premiers carrés parfaits!
les dix premiers carrés
parfaits sont :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 ) Citer les cinq premiers "cubes parfaits" !
|
|
|
|
|
|
5°) Donner (oralement )
les carrés des nombres suivants :
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
|
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
|
Il vous sera plus
commode d’utiliser les puissance de
dix : |
||||||||
|
1000 |
2000 |
3000 |
4000 |
5000 |
6000 |
7000 |
8000 |
9000 |
5 ) Calculer (sans
calculatrice)
|
Exemple : 42 = ? 4 |
5,1 |
|
22 = |
1,22 = |
|
32 = |
2,32 = |
|
42 = |
3,42 = |
|
122 = |
4,122 = |
|
1562 = |
51,1562 = |
|
4 |
5 |
|
23 = |
1,23 = |
|
33 = |
2,33 = |
|
43 = |
3,43 = |
|
123 = |
4,123= |
|
1563 = |
51,1563 = |
