|
|
|
|
Le "carrée"
parfait |
ENVIRONNEMENT du dossier:
|
1°)Racines carrés d’opérations simples |
2°) liste des objectifs sur les puissances et racines |
||
|
|
|||
|
|
|
|
|
|
|
|
|
|
DOSSIER:
RACINES CARREES d’un nombre entier ( N
) .
I ) « RACINE » d’un nombre
" : Nomenclature ( radicande ;
II ) « Racine carrée »
III ) Approximation de la racine carrée de
2 ; notée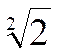 
ou 
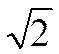
IV)
Valeur approchée et
encadrement d’une racine carrée.
|
écran |
COURS |
Interdisciplinarité |
|
||||
|
|
|
|
|
|
|
||
|
Travaux avec la
calculatrice : taper des
valeurs et comparer le résultat donné
par la table numérique |
|
Définition
de l’objectif : Savoir « donner » le radical d’un nombre.. (On dit aussi
donner la racine « carrée ou
cubique d’un nombre »)
Rappel nous abordons la racine carrée d’un nombre entier naturel ; ne pas confondre avec la racine
carrée d’un nombre relatif…
Partie 1 :
I ) « RACINE » Nomenclature
Le mot « Radical » est le nom donné au signe : 
Ce signe est constitué d’un « vé » prolongé
par une barre horizontale.(recouvrant totalement un
nombre ou une opération ).
Exemples :
; 
; 
; 
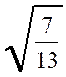
b ) « Radicande »
Le
nombre (ou opération) situé sous la
barre horizontale s’appelle : radicande
c ) Info sur les informations qui gravitent
autour du radical :
La barre horizontale
prolongeant le « vé » couvre la partie numérique(exemple
; ici 25 est
appelé le « radicande ».
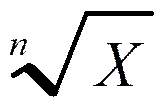
en prolongement de la branche
la plus courte du « vé »
(à gauche) de la pointe du « vé »
est inscrit un nombre ( « n » appelé
« indice ») ; il
indique le degré de la « racine » :
Quand
« n » vaut « 2 » on dit : « racine carré » ;
et l’on dit « racine cubique »
pour le nombre « 3 » , ou
« quatrième » pour le nombre
« 4 » ;ainsi de
suite.........
La pointe du « vé » étant sur la
ligne d’écriture.
Nota :
il est commun en collège de ne pas mettre le nombre «2 »
, et , on a décider
( ?) que l’on devait lire « racine carrée » à la vue de ce symbole :attention cela
n’est qu’une simplification d’écriture « 
» . Qu’il faudra
oublier au lycée.
La « racine carrée de 9 » s’écrit au collège 
alors que l’on
devrait écrire : 
PARTIE 2
II ) « RACINES CARRES»
PREALABLE:
il n ' y a pas de
"racine carrée d ' un nombre", si ce nombre n'est pas le carré d'un
autre .
Cas courants :
Il y a plusieurs modèles d’écritures mathématiques permettant d’indiquer que l’on veut connaître la racine
"carrée" d’un nombre :
A) Le plus courant au collège :
« Par convention »,au collège; on « simplifie » l’écriture , on n’inscrit pas la valeur
"2" sur la branche du vé
on dit i: « racine carrée de 25 » que
l’on traduit en écriture mathématique par « 
»
Racine
carrée .de « x » s’écrit
en mathématique 
B ) Deuxième écriture ;
au lycée:
Le nombre "2" apparaît sur
le vé .
Cela se traduit par : "faire la
« racine carrée » du nombre « 25 »"
que l’on traduit en écriture mathématique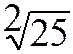 
Le
mot « carré » est à mettre en relation avec la leçon sur « périmètres ,aires et volumes.
« racine
carrée » du nombre «x » se traduit en
écriture mathématique par 
C )
Autre écriture utilisée :
(écriture utilisée
sur les calculatrices)
La racine carrée d’ un nombre est signifiée
aussi sous forme de puissance .(écriture qui sera
intéressante pour faire le calcul des "dérivées" )
On met le nombre sous forme
de puissance "fractionnaire"
de numérateur égale à 1 et de dénominateur égal à 2;
Ainsi :
devient
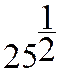lire: 25
« puissance un demi »
on peut dire aussi : Racine « un
demi » de 25.
CONCLUSION:
dans
tous les cas les trois écritures sont équivalentes ,elles ont la même signification.
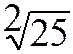: est égale qui est
égale à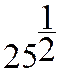
« Racine carrée
du nombre 25 ? » ( résultat = 5 )
Comment trouver la valeur de la racine carrée d'un
nombre ?
On
utilise souvent l'expression "faire
la racine carrée d’un nombre" ou "« extraire » la racine
carrée":
" Faire" la
« racine carrée » d’un nombre « X »(grand ixe )c’est c’ est rechercher le
nombre de départ ( sa racine! )« x » (petit ixe ) qui multiplié à lui même
(« x » (petit ixe) fois
« x » ( petit ixe ) a donné « X »(grand ixe).
Exemple: Faire la « racine carrée » d’un nombre
« 81 »(grand ixe )c’est c’ est rechercher
le nombre de départ «9x » (petit ixe ) qui multiplié à lui même
(«9x » (petit ixe) fois «9 »
( petit ixe ) a donné « 81 »(grand ixe).
Traduction en langage
mathématique:
Si 81 = 9
fois9 = 92; alors 9
= 
On
peut écrire :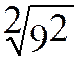 
= 9
A savoir :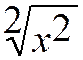 
= x
Comment obtenir la
valeur de la racine carrée d’un nombre?:
On nous dit que le nombre donné ( X ) est le « carré » d’un autre nombre( x ):
si l'on veut trouver la valeur de
« x » , il
faut faire la « racine carrée » de « X ».*
Pour
obtenir la valeur numérique de la racine carrée d’un nombre :
Il y a 4 possibilités:
1 )par calcul.(on dit "extraire
")
On dit dans ce cas que l'on va « extraire la racine
carrée »;la procédure permettant d’extraire la racine carrée d’un nombre ne sera pas traité dans
cet objectif.
2 )par
identification : reconnaît
des carrés parfaits ,on en déduit alors sa racine
Dans l’exemple:
on
connaît les carrés parfaits et alors on sait que 9fois9 est égal à 81;on
conclut que x = 9
,
3 )
par utilisation d’une table numérique Lil faut alors avoir à sa disposition une table
numérique , voir dans les livres de mathématiques.
la procédure
d’utilisation d’une table numérique n’est pas
prévue dans cet objectif.
4 ) ou utilisation de
la calculatrice.(c'est le cas le plus courant ,)
Exemple
d’exercice de recherche de la racine d'un nombre avec une calculatrice :
Question : Donner la valeur de la racine carrée de 81;
à l'aide d'une calculatrice.
Résolution:
a) On sait que 
= x (parce que l’on sait .....!)
b) On pose : X =
81 ; et l’on remplace X dans l’égalité
précédente
on peut écrire que :
x= 
c) il ne reste
plus qu'à recherche de la valeur
numérique : de
« x » (voir les possibilités)
Utilisation de la
calculatrice :
Procédure:
(En règle générale il y a sur les
calculatrices deux possibilités
, il faut utiliser la notice
du
fabriquant
)
a
) soit en utilisant la
touche 
taper 8 et 1 puis
sur la touche :résultat affiché :
9
b
) soit en utilisant la touche
: 
ou
|
Procédure
pour obtenir la racine « carrée » à la calculatrice : |
|
|
a) traduire « racine carrée de 81 » : |
811/2 |
|
b)taper |
8 et 1 |
|
c)taper sur la touche |
INV. |
|
d)taper sur la touche |
x 1/y
ou y 1/x |
|
f)taper le nombre
|
2 |
|
g)taper sur le signe
|
= |
|
h)
lire le résultat sur l’écran: |
9 |
INFO (s):
1°)
si 3 2 (tris au carré)
est égal 9
, on dira que « 
» (neuf puissance un demi) est égal à
3
2°) Exercices les plus exécutés:
|
Soit
une valeur de x |
on
pose x y |
le
résultat de x y est = X |
on
fait le calcul de |
le
résultat de |
soit
|
si x
= |
x y = X |
calculons X |
|
|
|
5 |
52 |
25 |
|
|
|
3 |
33 |
27 |
|
|
|
7 |
74 |
2401 |
|
|
=
=Commentaires:
a)
s’ il n’y a pas de difficulté à calculer la puissance
d’un nombre (x y ); il n’en est pas de même pour calculer la racine nième d’un
nombre (cela est plus difficile !)
b ) lorsque sous la racine il y a des nombres séparés
par des signes opératoires ; que faut -il faire avant de « rechercher »
la racine ?
il
faut effectuer l’opération ; Il ne
doit rester qu'un nombre sous la racine !
Si sous le radical il y a
des opérations ,il faut faire "en priorité"
le ou les calculs sous la racine , pour n'avoir plus qu'un seul nombre..
Exemples:
|
|
transformation |
Réponse(affichage à l'écran) |
|
|
|
19,416488 |
|
|
|
10,246951 |
|
|
|
181,04143 |
|
|
|
1,331187 |
Pour vérifier il faudrait
« élever » la "réponse au
carrée":
Exemple
: 19,4164882 = 377,00001 ; et
conclure que 19,416488 » 
C )
Sous la racine on a une inconnue "x" , il faudra donc
« résoudre » , comment faudra t -il
procéder pour isoler ? (exemple: 5 = 
)
Si nous avons une
racine carrée dont le radicande possède une inconnue « x » il faudra
« élevé » au « carrée » ,les
deux membres de l’égalité.(cas rencontré dans
« Pythagore »)
Résultats
à connaître « par cœur »:
1° ) La racine carrée de 2
vaut 1,414 ( voir
le calcul de la longueur de la diagonale d’un carré) et 
= 1,732 (utile pour un calcul dans le triangle)
2°)
Les racines carrées des carrés
parfaits sont :
Carrés parfaits
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
III ) Approximation de la racine
carrée de 2 ; notée 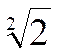ou :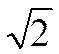
|
Construction de |
|
|
A partir d’un segment OA de longueur 1 , on construit la perpendiculaire ( D) passant par A .
On porte sur (D) le point B tel que AB = 1 D’après le théorème de Pythagore , le segment OB est de longueur |
|
a)
Avec la table : le résultat
de 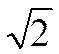: est donné avec 3 chiffres exacts après la
virgule : 1,
414
b ) Avec les calculatrices actuelles il est
possible d’obtenir de 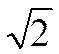avec une valeur avec
12 chiffres exacts après la virgule :
1,41413562373……
c)
Pour obtenir ces décimales ; un
procédé courant en mathématiques consiste à trouver une suite de nombres
( en général des rationnels) x0 , x1 ,x2 ,x3 , etc.. ; se rapprochant de plus en plus de la valeur cherchée
Ici par exemple ,
on peut choisir x0 = 1
Puis
x1 = 
( x0 +
) ; on obtient alors la valeur suivante :
1,5
Puis
x2 = ( x1 +
) ; on obtient alors la valeur suivante :
1,41666..
Puis
x3 = ( x2 +
) ; on obtient alors la valeur suivante :
1,4142156863
Etc.
Commentaire : comment sait-on que les nombres xn se
rapprochent de 
au fur et à mesure que
« n » augmente. ? Sans
entrer dans le détail , nous pouvons indiquer qu’une
des propriétés utilisées ici est que 
est solution de
l’équation x = ( x +
)
d ) Une autre possibilité est le calcul en posant l’opération appelé « extraction
d’une racine carrée »
Extraire la racine carrée d’un nombre c’est trouver
la racine carrée de ce nombre
IV ) Valeur approchée et
encadrement d’une
racine carrée
Pré requis : arrondir et troncature
Sur la calculatrice , on lit 
= 2,236 067 978 ….
En général il est inutile de donner toutes les décimales.
Mais on peut affirmer par exemple que : 2,236 < < 2,237
On dit que l’on a un encadrement de d’amplitude 0,001 .
2,236 est une valeur approchée par défaut à 10-3 prés (par excès)de
2,237 est une valeur approchée par excès à 10-3 prés (par défaut)de
Plus
généralement :
Si a - 10-n £ x £ a + 10-n
On dit que « a » est une valeur approchée de « x » à
la précision : 10-n
Autres
exemples :
|
Encadrement
d’amplitude 10-4 de |
Calculatrice :
donc 44,6989£ |
|
Encadrement d’amplitude
10-4 de |
Calculatrice :
donc : 0,2345£
|
TRAVAUX AUTO FORMATIFS.
Partie 1
1°) Dites tout ce que
vous savez sur ce symbole:
2°) Que désigne le
mot « radical » ?
3°) Que désigne le
mot « radicande » ?
Partie
2 : LES
RACINES CARREES.
4°) Donner les trois écritures utilisées en
mathématique pour indiquer que l’on désire connaître la valeur de la racine carrée d’un nombre.(prenez le nombre :
36 )
*on ne vous demande pas de faire le calcul !
5°) Traduire en
langage littéral ,
donner son utilisation :
"ixe" puissance
un sur i grec
ou 
traduire :
:
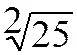est
égale 
est égale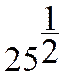 
6°) Que cherche - t - on
à obtenir lorsque
l’on veut connaître la racine carrée d’un nombre ?
7°) Quelles sont les
différentes façons de connaître la racine carré d’un nombre ?
*cela sera
vraie pour tous les cas de recherche de la valeur des
« racines ».
8°) Donnez la
procédure permettant d’obtenir la racine carrée d’un nombre à la calculatrice!
(Il en existe deux
.......).
9°) sous la racine il y a des nombres
séparer par des signes opératoires ; que faut –il faire avant de
rechercher la racine ?
10°) Sous la racine
on a une inconnue , il faudra donc
« résoudre » , comment faudra t –il
procéder pour isoler ?
1° ) Trouver les racines carrées parfaits des multiples de
dixLavec la calculatrice)
de 100 à
10 8
si elles existent ! pour
100
;101 ; 102 ; 103 ; 104 ; 105 ; 106 ;10 7 ; 10 8;
2°)
soit un nombre « x » ; trouver
la racine carrée du nombre :
x
= 7,29 ; 
=
x
= 33,64 ; =
x
= 81 ; =
x
= 291 600 ; =
x
= 2 744 000 ; =
x
= 1,5746
108 ;
=
3
° ) Faire les calculs suivants à l’aide d’une
calculatrice ;donner le résultat avec la précision du dixième
=
=
=
4
° ) Faire les calculs suivants à l’aide d’une
calculatrice ;donner le résultat avec la précision du centième
=
=
(faire
d’abord le calcul sous le radical )
=
5 °) Faire les calculs suivants à l’aide
d’une calculatrice ;donner le résultat avec la
précision du millième ((faire d’abord le calcul sous le radical)
=
=
=
=
=
6°)
Donner, de mémoire, la racine carrée des
nombres suivants:
16 ;
36 ; 81 ; 25 ;
49 ; 4 ; 1 ;
9 ; 144
; 121 ; 64 ; 100 ;
7° ) Donner la valeur de la racine carrée de
"2" et de "3" .:
8°)
donner le résultat de la racine carrée des nombre suivants :
|
|
|
|
|
|
|
|
|
|
|
|
= ____________________ à 0,001 près( Résultats dans le cours)
Compléter
le tableau suivant :
Interdisciplinarité:
Les racines en sciences
En science on utilise l’écriture m1 ; m2 ; dans quelle activité ,
préciser , comment passe-t-on de l’un à l’autre
?
|
Calcul
d’ aire d’un carré : et inverse |
|
|
|
