|
DOSSIER : LES
RACINES / objectif cours 10 |
|
Pré requis
|
Produits de
nombres relatifs |
Environnement du dossier
|
Objectif
précédent : |
Objectif
suivant : |
|
COURS |
Interdisciplinarité Exemple :Recherche
de l’arête d’un cube.. |
|
Applications
de la racine cubique aux sciences : (volume)
Rappels:
Définition de l’objectif : Savoir « donner » le
radical d’un nombre..
(On dit aussi
donner la racine « carrée ou
cubique d’un nombre »)
a)
« Radical »
Le mot
« Radical » est le nom
donné au signe : ![]()
Ce signe est constitué d’un « vé » prolongé
par une barre horizontale.(recouvrant totalement un nombre ou une opération ).
Exemples :
![]() ;
; ![]() ;
; ![]() ;
; 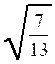
b )
« Radicande »
Le nombre (ou opération)
situé sous la barre horizontale s’appelle : radicande
c ) Ce
qui gravite autour de ce signe :
![]() la
barre horizontale prolongeant le « vé » couvre la partie numérique(exemple
la
barre horizontale prolongeant le « vé » couvre la partie numérique(exemple![]() ; ici 25 est le radicande ).
; ici 25 est le radicande ).


![]()
![]()
![]()
sur la branche la plus courte du « vé » (à gauche) est
inscrit un nombre
; (qui
indique
le dégré de la racine carré pour le nombre (2) ;cubique pour le nombre (3) , ou quatrième pour
le nombre (4) ;ainsi de
suite.........
La pointe du vé étant sur la ligne d’écriture.
Racine
CUBIQUE : OBTENTION d’une racine cubique d’un nombre
dans tous les cas les écritures sont équivalentes
: ![]() est
égale
est
égale 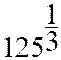
![]() : Le nombre
« 3 » apparaît toujours , dans ce cas on dit
que l’on calcule la « racine cubique »;ou « racine troisième »
: Le nombre
« 3 » apparaît toujours , dans ce cas on dit
que l’on calcule la « racine cubique »;ou « racine troisième »
Procédure pour obtenir
: ![]()
a) traduire « racine cubique
de 125 » : ![]() en « 125 puissance un tiers » : 1251/3
en « 125 puissance un tiers » : 1251/3
b)taper
1et 2 et 5
c)taper sur la touche INV.
D)taper sur la touche x 1/y ou y 1/x
f)taper le nombre
3
g)taper sur le signe
=
h) lire le résultat sur l’écran:
5
Applications
numériques:
Donner mentalement la racine cubique
de:
1000 ; 8 ;
27 ; 81 ; 125 ; 64
Avec la calculatrice :
faire les racines cubiques de : 9 938 ,375 ; 13 500 ; 405 224 ; 1 000 000
Applications:
GEOMETRIE:
Comment obtenir la valeur d’une racine d’un nombre ?
TRAVAUX AUTO FORMATIFS.
1°) Dites tout ce que vous savez sur ce symbole:
![]()
2°) Que désigne le mot « radical » ?
3°) Que désigne le mot « radicande » ?
LES RACINES CUBIQUES.
9° ) Donnez
les deux écritures mathématiques
indiquant que l’on recherche la racines cubique d’un nombre .
10 °) Donner la procédure qui permet d’obtenir la valeur de la racine cubique d’un
nombre avec la calculatrice .
11 °) Constat: comparer la procédure utilisée avec
celle utilisée pour calculer le racine
carrée !
12 °) Application aux sciences : cas des
m3.
a ) Que désigne le mot
« grandeur »
b )
Dans quel domaine utilise-t-on la grandeur
« m 3 » ?;
c) comment passe-t-on de m3 à m1 (m) ?
c) comment
passe t - on de m3 à m2 ?
(attention ,il faut réfléchir davantage ! )
Transformer Faire : ![]() ;
; ![]()
Trouver les racines cubiques parfaits des multiples de dix:
de 100
à 10 9
|
100 |
|
|
101 |
|
|
102 |
|
|
103 |
|
|
104 |
|
|
105 |
|
|
106 |
|
|
10 7 |
|
|
10 8 |
|
|
10 9 |
|
Série d’exercices: Donner une valeur approchée d’une racine d’un nombre
1 ° ) Calculer les expressions suivantes
avec la précision du dixième
|
|
Résultat calculatrice |
Au dixième |
|
|
|
|
|
|
|
|
|
|
|
|
2 ° ) Calculer les expressions
suivantes avec la précision du
centième
|
|
|
|
|
|
|
|
|
|
|
|
3 °) Calculer les expressions
suivantes avec la précision du millième
|
|
|
|
|
|
4,4647451 |
4,465 |
|
|
21,111276 |
21,111 |
|
|
4,3742992 |
4,37 |
|
|
4,717694 |
4,718 |
|
|
2,6754054 |
2,675 |
ENCADREMENT D’UN RESULTAT :
Dans les exercices suivants :
Donner le résultat sous la forme:
n < ![]() <n+1
<n+1
ou n est un entier naturel et X un nombre (entier
ou décimal )
|
4 |
|
5 |
|
21 |
|
22 |
|
4 |
|
5 |
|
4 |
|
5 |
|
2 |
|
3 |
Volume : calcul de l' arrête d'un cube
Application de la racine cubique en sciences
Calcul de volumes: le nombre donné (125 ) est le résultat d’un calcul du
volume d’un cube :125 m3
Type
d’exercice : Rechercher la longueur
du coté d’un cube ( petit cé « c »)dont on connait son volume (cé au cube qui s’écrit: c 3
).
Type
d’énoncé :
Le volume d’un cube est de 125 m3 ( on devrait
dire:125 fois 1 m3 (mètre cube);ce qui pourrait s’écrire 125![]() m3
m3![]() .
.
Résolution:
rappel
On sait que le volume d’un cube est égale à la surface de base du cube multiplié par la longueur d’un coté
(ou hauteur) ou « coté fois coté fois coté » ;le
coté étant à la fois un nombre et une unité:
*un nombre a qui on associe une unité est appelé : GRANDEUR
( 5 m 1
par 5 m 1 par 5 m 1
= 125 m 1 par m1 par m 1)
soit les opérations :
5
fois 5 = 25 ; 25 fois5 =125
et m1![]() m1 = m2 ; m2
m1 = m2 ; m2![]() m1 = m3
m1 = m3
dans le calcul des puissances nous avons vu que : m1![]() m1 = m 1+1
= m2
m1 = m 1+1
= m2
et que m2![]() m1 =m2+1 = m3
m1 =m2+1 = m3
![]() je peux donc écrire que *
je peux donc écrire que * ![]() = m1
= m1
On sait que
pour « Rechercher la longueur du coté d’un cube ( petit cé
« c »)dont on connaît son volume (cé au cube c 3 ). » il suffit de faire la racine cubique
de (cé au cube c 3
). ce
qui se traduit par l’écriture mathématique: ![]()
Comme c 3=125![]() m3
m3![]() .
.
pour trouver « c »; j’écrierai
que ![]() =
= ![]()
c = ![]()
c =![]()
Calcul : ![]() se décompose en un produit
se décompose en un produit ![]() ,je calcule donc indépendamment
,je calcule donc indépendamment
![]() et
et ![]() ;
;
![]() je peux donc écrire que *
je peux donc écrire que * ![]() = m1
= m1
et que ![]() = 5
= 5
Résultat: ![]() = 5
= 5![]() m1
m1
soit plus simplement : 5
m
conclusion :le cube de 125 m3
à pour coté 5 m , on dit, aussi, 5 mètre d ’arrête.