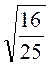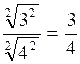Pré requis:
ENVIRONNEMENT du
dossier:
|
Info
complémentaire : 2 Puissances et
racines niveau V . Liste des cours en
calcul numérique |
|||
|
|
|||
DOSSIER: Niveau III : LA RACINE nième
· La racine de certain nombre est dit : nombre « incommensurable »
· L’extraction de la
racine est appelée : la sixième opération en mathématique · Définitions :
a) « Radical » . b )
« Radicande » . c )
Ce qui gravite autour de ce signe d) Les nombres dits « Irrationnels ». · CAS GENERAL: RACINE nème
d’un nombre · OBTENTION DE
LA RACINE N ièmè D’UN NOMBRE · RACINES D' UN NOMBRE
RELATIF · Relations
entre les écritures mathématiques
de la "RACINE N ièmè " et la " PUISSANCE N ièmè
" D’UN NOMBRE et
d'une opération simple ·
Généralisation sur les racines… |
||||||||
|
COURS
|
|
|||||||
La racine de certain nombre est dit : nombre « incommensurable »
|
||||||||
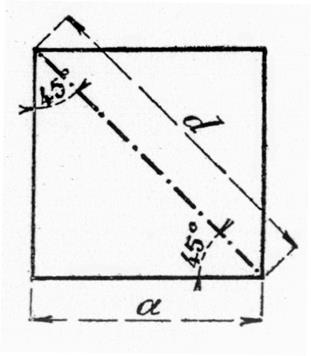
Exemple :
Si l’on mesure la diagonale « d » d’un carré en prenant comme unité de mesure
le côté « a », on ne trouve aucune partie de l’unité
« a » contenue un nombre exact de fois dans « d » , on
dit qu’il n’y a pas de « commune » mesure entre « d » et « a » ,
le résultat de la mesure est un nombre incommensurable . Dans le cas de la
figure ce nombre est Dans la pratique des opérations
, on se contente d’une mesure
approchée de la grandeur donnée et l’approximation varie avec la nature de la
mesure à effectuer. |
|
|||||||
Cas Général : la racine nième
L’extraction de la racine est appelée : la
sixième opération en mathématique ;
Définition
de l’objectif : Savoir « donner » le radical d’un nombre.. (On
dit aussi donner la racine « carrée
ou cubique d’un nombre »)
a) « Radical »
Le mot « Radical »
est le nom donné au signe : ![]() , Ce
signe est une modification de la lettre
« r » , initiale du mot latin qui signifie « radical ».
, Ce
signe est une modification de la lettre
« r » , initiale du mot latin qui signifie « radical ».
On trace un « vé » prolongé par une barre horizontale.(recouvrant totalement un nombre ou une opération ).
Au XVIème
siècle encore , on se servait ,pour désigner la racine
, d’un « R » majuscule , suivi d’un « q » ou d’un
« c » pour indiquer respectivement la racine carrée (quadrus) ou cubique (cubus) .
Par exemple on écrivait R.q. 1225 au lieu de la notation ![]() ,
,
Exemples :
![]() ;
; ![]() ;
; ![]() ;
; 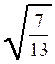
b ) « Radicande »
Le nombre (ou opération) situé sous la barre horizontale s’appelle : radicande
c ) Ce qui
gravite autour de ce signe ![]() :
:
![]() la
barre horizontale prolongeant le « vé » couvre la partie numérique(exemple
la
barre horizontale prolongeant le « vé » couvre la partie numérique(exemple![]() ; ici 25 est le radicande ).
; ici 25 est le radicande ).


![]()

![]()
sur la branche la plus courte du « vé » (à gauche) est
inscrit un nombre appelé « indice » ; (il
indique
le degré de la racine carré pour le nombre (2) ;cubique pour le
nombre (3) , ou quatrième pour le nombre
(4) ;ainsi de suite.........
La pointe du vé étant sur la ligne d’écriture.
|
d) Les nombres dits « Irrationnels » |
|
|
Les nombres tels que |
Remarques : |
*Les irrationnels
appartiennent à l’ensemble des nombres dits « Réels ». (cliquez
ici ++++)
CAS GENERAL: RACINE nème
d’un nombre
La « racine » d’un nombre « X » est l’opération
inverse de la puissance qui tend à trouver le nombre « x »de départ
qui à permit de calculer X .
en faisant le calcul de xn on obtient un nombre " X "
donc
inverse en faisant le calcul X1/n
on retrouve le nombre
" x"
En ayant
« X » est
« n » ;on
demande de retrouver « x » ; pour cela on utilise l écriture
( sachant que l’on a admis que xn =X )
Remarque:
On écrit aussi que :
![]() =
= 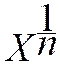 ; ces deux écritures mathématiques ont la
même signification;(écriture utilisée
dans l'objectif « dérivation » )
; ces deux écritures mathématiques ont la
même signification;(écriture utilisée
dans l'objectif « dérivation » )
Remarques :
les
écritures de la forme 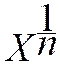 ;telle
que
;telle
que ![]() et
et
![]() sont souvent utilisées sur les
calculatrices (pour effectuer la même opération ,cela dépend des marques
).
sont souvent utilisées sur les
calculatrices (pour effectuer la même opération ,cela dépend des marques
).
A savoir :
-S i x y = X , alors
x = ![]()
(traduction
: si le nombre petit « ixe » à la puissance y a pour résultat ( est
égal ) le nombre grand « ixe » ,alors le nombre petit « ixe » est égal à la racine hi grec ième
du nombre grand « ixe ». )
Exercices les plus exécutés:
|
Soit une valeur de x |
on pose x y |
le résultat de x y est
X |
on fait le calcul de (lire :racine nième ) |
le résultat de |
soit
|
si x = |
x y |
calculons X |
|
= x |
|
5 |
52 |
25 |
|
= 5 |
|
3 |
33 |
27 |
|
= 3 |
|
7 |
74 |
2401 |
|
= 7 |
Commentaire:
il n’y a pas de difficulté à calculer la puissance d’un nombre (x y );il n’en est pas de même pour calculer la
racine nième d’un nombre :
Comment obtenir la valeur
d’une racine d’un nombre ?
· OBTENTION DE LA
RACINE N ièmè D’UN NOMBRE
Pour obtenir la racine nième d’ un nombre ( exemple : ![]() ) il y a plusieurs
possibilités:
) il y a plusieurs
possibilités:
a) soit par le calcul:
il est possible de
calculer la racine carré d’un nombre; cela fait l’objet d’une leçon
particulière.(c’est le seul cas de calcul qui peut
être accessible à un élève).
b) Soit par identification: il faut connaître et
donc reconnaître les carrés parfaits.
c) Pour tous les autres cas il vous faut consulter une table numérique (recensant
tous les calculs faits à l’avance )
d) ou alors il vous
faut apprendre à utiliser la
calculatrice.
Autres écritures
utilisées par les calculatrices: signifiant que l’on calcule le radical
d’un nombre.
a) ![]() est = à
est = à
![]() . (que l’on traduit
par « racine » y ième de X )
. (que l’on traduit
par « racine » y ième de X )
b) ![]() est =
à
est =
à ![]() . (que l’on traduit
par « racine » x ième de y )
. (que l’on traduit
par « racine » x ième de y )
· RACINES
D' UN NOMBRE
RELATIF
Deux cas renfermant deux cas :
|
|
|
||
|
"x" est positif |
"x"
est négatif |
"x" est positif |
"x" est négatif |
|
Exemple: Résultat = (+5) |
Exemple: Résultat impossible; le carré
d'un nombre est toujours positif |
Exemple : Résultat : (+3) |
Exemple : Résultat : (-3) |
|
Calcul possible |
Calcul impossible |
Calcul possible |
Calcul possible |
Cas d'un calcul courant
d'algèbre à maîtriser :
|
On
donne x 2 = (+25) ; quelle
est la valeur de "x" ? Réponse : "x" vaut (+5) ou (-5) Raison : (+5)(+5) =(+25) ; (-5)(-5) =
(+25) |
Réponse: on fait la racine carrée de
"25" ; on trouve
"5" "5" est la valeur absolue de
"x" ; conclusion ;on peut
donner deux valeurs à "x": x= (+5) x= (-5) |
de calcul :
· Relations entre
les écritures mathématiques de la "RACINE N ièmè
" et la " PUISSANCE N ièmè " D’UN NOMBRE et d'une opération simple
|
EN RESUME : |
|
|
|
|
Rappel xn |
Peut s'écrire = |
|
|
|
Ecriture avec le radical : |
Ecriture équivalente Sans radical
|
Développement ou simplification : |
résultat |
|
|
|
|
|
|
( |
(x |
x |
x1 = x |
|
( |
((x n ) |
((x |
= x n |
|
|
(x |
x |
|
|
x |
|
|
|
|
|
( |
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aucune transformation possible |
(x + y) |
|
|
|
Aucune transformation possible |
x |
|
|
|
Aucune transformation possible |
(x - y) |
|
|
|
Aucune transformation possible |
x |
|
|
|
|
|
|
|
·
Généralisation sur les racines |
· Ecritures équivalentes : ![]() =
= ![]() =
= ![]()
· Si a ³
0 , alors ![]() désigne le seul nombre qui a pour carré
« a ».
désigne le seul nombre qui a pour carré
« a ».
Exemples
« 16 » est un nombre positif ,
le nombre positif qui a pour « carré » « 16 » est
« 4 ».
On sait que : ( 4²
= 4 ´ 4 =
16 ) ;
On dit que « 4 » est la racine
carrée de « 16 » et on écrit : ![]() = 4
= 4
21 est
un nombre positif , sa racine carrée n’est ni un
nombre entier ni un nombre décimal , ni une fraction , on l’écrit : ![]()
iCe
nombre qui n’est ni un nombre entier , ni un nombre décimal , ni une fraction est
appelé : nombre « irrationnel ».
· Si a ³
0 , alors (![]() )
² = a
)
² = a
· Si a ³ 0 ,
alors ![]() est la solution positive de l’équation x² = a
est la solution positive de l’équation x² = a
Conséquences :
·
Si k ³ 0 ,
alors ![]() = k et , si
k £ 0 ,
alors
= k et , si
k £ 0 ,
alors ![]() = - k
= - k
Exemple :
( + 4 ) ² = (+16 ) et ( -
4 )² = ( + 16 ) aussi si l’on fait la racine carré du nombre relatif ( +16) : on trouve deux
solutions possibles :
![]() = ( + 4 ) ou ( - 4)
= ( + 4 ) ou ( - 4)
· Si a
³
0 et
b > 0 alors
- Le produit
de deux racines carrées est égal à la racine carrée des produits
![]() ´
´ ![]() =
= ![]() ( =
( = ![]() )
)
Exemple :![]() ´
´
![]() =
= ![]() =
= ![]() = ( 3 ´
10 = 30)
= ( 3 ´
10 = 30)
· Si a
³
0 et
b > 0 alors
La racine
carrée d’un quotient est égale au quotient des racines carrées
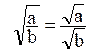
Exemple 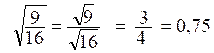
· L’équation
x² = a
- Si a < 0,
elle n’a pas de solution.
- Si a = 0,
elle a pour seul solution « 0 » .
- Si a >
0, elle a deux solutions + ![]() et -
et -![]() .
.
TRAVAUX AUTO FORMATIFS.
CONTROLE
Que signifie: calculer le radical d’un nombre ?
La « racine » d’un nombre
« X » est l’opération inverse de la puissance qui tend à trouver le
nombre « x »de départ qui à permit de calculer X .
Donner l’écriture utilisée sur les calculatrices pour effectuer la recherche d’un radical d’un
nombre.
![]() = x =
= x = 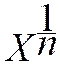 ;telle
que
;telle
que ![]() et
et
![]()
Quelles sont les possibilités d’obtenir la valeur
numérique de la racine n ième d’un nombre ?
Ecrire différemment
les expressions suivantes : (forme d'écriture :
puissance )
|
|
|
|
|
|
Rappel xn |
|
|
|
|
Ecriture avec le radical : |
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rappel xn |
Peut s'écrire = |
|
|
|
Ecriture avec le radical : |
Ecriture équivalente Sans radical
|
Développement ou simplification : |
résultat |
|
|
x |
|
|
|
( |
(x |
x |
x1 = x |
|
( |
((x n ) |
((x |
= x n |
|
|
(x |
x |
|
|
|
x |
|
|
|
|
( |
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aucune transformation possible |
(x + y) |
|
|
|
Aucune transformation possible |
x |
|
|
|
Aucune transformation possible |
(x - y) |
|
|
|
Aucune transformation possible |
x |
|
|
|
|
|
|
Trouver les racines carrées parfaits des multiples de dix:
de 100 à 10 8
si elles existent ! pour 100 ;101
; 102 ; 103
; 104 ; 105 ; 106 ;10 7 ; 10 8;
Première série d ’exercices :
soit un nombre « x » ;
trouver la racine carrée du nombre :
x =0.25 ; ![]() =
=
x = 7,29 ; ![]() =
=
x = 33,64 ;
![]() =
=
x = 81 ; ![]() =
=
x = 291 600
; ![]() =
=
x = 2 744 000
; ![]() =
=
x = 1,5746![]() 108 ;
108 ; ![]() =
=
II )Deuxième série d’exercices en
relation avec la racine carrée d’un
produit:
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() =
=
![]() =
=
donc : ![]() =
=![]() =
=
III ) Troisième série d’exercices en relation avec la racine d’un quotient:
Ces exercices utilisent des carrés parfaits
![]() =
=
![]() =
=
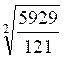 =
=
Se ramener aux carrés parfaits; en se souvenant que
tout nombre « à virgule » peut se mettre sous forme de fraction de
dénominateur égal a ...........
![]() =
=
![]() =
=
IV ) Quatrième série d’exercices en
relation avec la racine carrée d’une
addition ou d’une soustraction , et les transformations
a) ![]() =
=
b ) ![]() =
=
c ) ![]() =
=
d ) ![]() =
=
e ) ![]() =
=
f ) ![]() =
=
g ) ![]() =
=
h ) ![]() =
=
k ) ![]() =
=
V ) Cinquième série
d’exercices: Donner une valeur approchée d’une racine d’un nombre
1 ° ) Calculer les
expressions suivantes avec la précision
du dixième
![]() =
=
![]() =
=
![]() =
=
2 ° ) Calculer les
expressions suivantes avec la précision
du centième
![]() =
=
![]() =
=
![]() =
=
3 °) Calculer les expressions suivantes avec la précision du millième
![]() =
=
![]() =
=
![]() = =
= =
![]() =
=
![]() =
=
I ) remplacer dans les lettres par les nombres
suivants et faire le calcul :
avec x= 16
et y = 9 (remarque : 16 et 9 sont
des carrés parfaits; nous connaissons la racine carrée de 16 (4) et de 9 (3) , ces valeurs sont choisies pour faciliter la
compréhension)
|
|
|
|
|
|
( |
( |
|
|
|
( |
( |
|
|
|
|
|
|
|
|
|
= = 4 = 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Le calcul est impossible |
On ne peut faire la racine carré d'un
nombre négatif ! |
|
|
|
|
|
|
|
|
|
|
II ) Transformer en vue de
simplifier les calculs :
|
|
|
|
|
|
|
5 |
|
|
|
2 |
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 + 4 = 7 |
|
|
|
|
|
|
- |
= 3-4 |
|
|
( |
= 81 |
|
III) Résoudre :
|
: 7
= |
7 2 = ( |
: 7 2 = 30+x 49 = 30+x 49 - 30 =
x ;
19 = x ; conclusion « x » vaut 19 |
|
50 = |
50 2 = ( |
50 2 =1600+x2 2500 - 1600
= x2
30 = x |
CALCULS:
A ) Trouver les racines carrées parfaits des multiples de dixLmettre une croix dans la case correspondante
|
|
|
|
|
100 |
|
|
|
101 |
|
|
|
102 |
x |
|
|
103 |
|
|
|
104 |
x |
|
|
105 |
|
|
|
106 |
|
|
|
10 7 |
|
|
|
10 8 |
x |
|
B ) soit un nombre « x » ;
trouver la racine carrée du nombre :
|
|
|
|
|
x =0,25 |
|
0,5 |
|
x = 7,29 |
|
2,7 |
|
x = 33,64 |
|
5,8 |
|
x = 81 |
|
9 |
|
x = 291 600 |
|
540 |
|
x = 2 744 000 |
|
1656,502339 |
|
x = 1,5746 |
|
39681,22982 |
C )Deuxième série d’exercices en relation avec la
racine carrée d’un produit:
|
|
|
|
|
|
|
4 fois 5 =20 |
|
|
|
|
|
|
|
|
|
|
|
=630 |
|
|
|
=1600 |
|
|
|
=600 |
D ) Troisième série d’exercices en relation avec avec
la racine d’un quotient:
Ces exercices utilisent des carrés parfaits
|
|
|
|
|
|
|
1,6 |
|
|
|
1,5 |
|
|
|
7 |
E ) Se ramener aux carrés parfaits; en se souvenant que tout nombre
« à virgule » peut se mettre sous forme de fraction de dénominateur
égal a ...........
|
|
|
9,3 |
|
|
|
0,86 |
F ) Quatrième
série d’exercices en relation avec la
racine carrée d’une addition ou d’une
soustraction , et les transformations
|
|
|
|
|
|
|
6,32455532 |
|
|
|
37,74917218 |
|
|
|
5,385164807 |
|
|
|
9,219544457 |
|
|
|
44,82186966 |
|
|
|
8,136952747 |
|
|
|
65 |
|
|
|
57 |
|
|
|
55 |
G ) Cinquième
série d’exercices: Donner une valeur approchée d’une racine d’un nombre
1 ° ) Calculer les
expressions suivantes avec la précision
du dixième
|
|
|
|
|
|
|
2,2 |
|
|
|
4,1 |
|
|
|
69,0 |
2 ° ) Calculer les
expressions suivantes avec la précision
du centième
|
|
|
|
|
|
|
4,80 |
|
|
|
94,00 |
|
|
|
9,15 |
3 °) Calculer les expressions suivantes avec la précision du millième
|
|
|
|
|
|
|
9,434 |
|
|
|
9,7417 |
|
|
|
9,149 |
|
|
|
10,247 |
|
|
|
4,376 |
|
|
|
impossible |
H ) ENCADREMENT D’UN RESULTAT
:
On donne le
résultat des exercices suivants :
![]() =4,4647451
=4,4647451
![]() =21,111276
=21,111276
![]() =4,3742992
=4,3742992
![]() =4,717694
=4,717694
![]() =2,6754054
=2,6754054
![]() = -3
= -3
Donner le
résultat sous la forme: n <
![]() < n +1
< n +1
ou n est un entier naturel et X un nombre (entier
ou décimal )
|
: n |
< |
|
< |
n +1 |
|
4 |
|
|
|
5 |
|
21 |
|
|
|
22 |
|
4 |
|
|
|
5 |
|
4 |
|
|
|
5 |
|
2 |
|
|
|
3 |
|
-4 |
|
|
|
-3 |