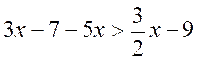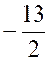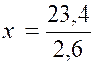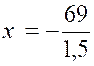On appelle « inégalité du premier degré » , une inégalité dans laquelle figure , outre les quantités connues , une inconnue (ou variable) « x » , au premier degré

Par exemple , l’inégalité :

Est une inégalité du premier degré en « x »

Remarquer qu’il serait plus correct d’employer, concurremment avec le mot « inégalité » , les termes « inéquation » et « in identité » d e même qu’on emploie , concurremment avec « égalité » , les termes « équation » et « identité ».

Une « in identité » est une inégalité toujours vérifiée quelles que soient les valeurs numériques données aux lettres qu’elle peut contenir.

Une inéquation est une inégalité qui n’est vérifiée que pour certaines valeurs particulières données aux lettres et qui sont les solutions de cette inégalité.

Nous nous conformerons à l’usage le plus répandu , ce qui n’a pas d’inconvénient dans les questions élémentaires que nous allons traiter .

3°) Résolution :

· Par définition : Résoudre une inégalité, c’est déterminer pour quelles valeurs de « x » elle est satisfaite.

· Les théorèmes relatifs aux inégalités :

Les théorèmes relatifs aux inégalités permettent des transformations analogues à celles que nous employons pour les « égalités »

Théorèmes « égalités »

SOS rappels

Ainsi ,on peut, pour les inégalités comme pour les égalités , faire passer un terme d’un membre dans l’autre en changeant son signe, et procéder aux simplifications visibles « a priori » que nous avons indiquées pour les équations ,à savoir : suppression des termes identiques dans les deux membres , suppression d’un facteur commun à tous les termes (à condition que ce facteur soit positif ) , etc.

On pourra aussi chasser les dénominateurs.

Les inégalités du premier degré à une inconnue se résolvent donc par une marche tout à fait semblable à celle que nous avons indiquée pour les équations, et la règle de résolution serait aisée à formuler 0.

Il faut seulement avoir grand soin de changer le sens de l’égalité lorsqu’on multiplie ou divise par un nombre négatif.

Si on multiplie ou si on divise les deux membres d’une inéquation par un même nombre :

%Ï strictement positif : on conserve le sens de l’inéquation.

%Ï strictement négatif : on change le sens de l’inéquation.

Soit , par exemple, à résoudre l’inégalité :

3 x - 5 > 5x + 8

on fait passer les termes renfermant les « x » dans le premier membre et les autres dans le second membre, elle devient :

-2 x >13

d’où en divisant par –2 : on doit changer le signe « > » en « < »

x < soit x <

ou x < -6,5

On a changé le sens , puisque –2 est négatif.

SOS rappel

On aurait pu utiliser cette remarque :

Qu’on peut dans une inégalité changer les signes de tous les termes à condition de changer le sens de l’inégalité.

On aurait eu : -2 x >13

2x < -13

x < - 6,5

l’ensemble des solutions : S = ] - ¥ ; - 6,5 [

· Solution graphique : la partie hachurée représente les non solutions ; la partie à droite de « 2,5 » représente l’ensemble des solutions , valeurs que peut prendre « x ».

A mettre le dessin ………..

4°) Exemples de résolutions

a) Résoudre : 4 x < 10

on divise par « 4 » : x < 2,5

Conclusion :

Première forme : x < 2,5 ( lire : « ixe » strictement inférieur à 2,5 ; soit : tous les « ixes » inférieurs à 2,5 )

Deuxième forme : ] - ¥ ; 2,5 [

Troisième forme :

Représentation graphique :

[

0 1 2,5

La partie hachurée représente les non solutions ; la partie à gauche de « 2,5 » représente l’ensemble des solutions , valeurs que peut prendre « x ».

b ) Résoudre : - 2 x £ 5

On divise par « - 2 » (on change le sens de la relation d’ordre) : x ³ - 2,5

Conclusion sur la présentation de la solution:

Première forme : x ³ - 2,5

Deuxième forme : [ –2,5 ;+ ¥ [

Troisième forme : représentation graphique :

[

-2,5 - 1 0

la partie hachurée représente les « non solutions » ; la partie à droite de « 2,5 » représente l’ensemble des solutions , valeurs que peut prendre « x ».

Activités : Résoudre dans R , les inéquations suivantes ( pour chaque exercice , donner l’ensemble des solutions sous forme d’intervalle et représenter cet intervalle sur une droite graduée.

c ) Résoudre - 4x < 5 Û x < - 1,2

Activités (suite) :

	Exercices	solution
1.
2.
3.		3x + 3 < x -2 ; 2 x < - 5 ; x < - 2,5
4.

Suite %º

Les systèmes d’inégalités à une inconnue

4°) Exemples de résolutions :

· Exemple 1
	Résoudre l’inéquation
	Résolution : 3x – 2 x + 8 + 5 x 13	Résolution pratique :: on ajoute « -2x » dans chaque membre. 3x – 5 – 2 x 2 x + 8 - 2 x 3x – 5 – 2 x + 8 + 0 on ajoute « +5 » dans chaque membre : 3x – 5 + 5 – 2 x + 8 + 5 on obtient : 3x + 0 – 2 x + 8 + 5
	Représentation graphique des solutions :
	Remarquez que le crochet indique que la valeur « 13 » est incluse comme solution….
· Exemple 2
	Résoudre l’inéquation 7x + 4 4 x + 19
	Après une double transformation : 7x – 4 x + 19 – 4 Ensuite après « regroupement » : 3x + 15 Soit :	Après réduction….
	Remarquez que le crochet indique que la valeur « 5 » est incluse comme solution….
· Exemple 3
	Résoudre l’inéquation 2x – 8 < x – 7
	Après une double transformation : 2x – x < -7 + 8 Ensuite après « regroupement » : x < 1
	Remarquez que le crochet indique que la valeur « 1 » est exclue comme solution….

TRAVAUX AUTO _ FORMATIFS

CONTROLE :

Dans une inégalité si l’on multiplie ou divise par un nombre négatif que faut – il faire impérativement ?

EVALUATION :

EVALUATION

Devoir : (corrigé dans le cours)

	Exercices	solution
1-	2x < 23,4
2-	-1,5 "e 69
3-	3 ( x + 1 ) "e x - 2
4-	> 4

Série 2 :

Résoudre les inégalités suivantes :	Rendre compte de trois façons différentes.
4 x < 10
- 2 x £ 5
3x – 3 > 5x -5
3x – 5 > x + 4
2x -< x +
4x + > x + 4

Série 3.

	Résoudre :	Résolution
1-a	5x – 7 < 1
1-b	-2x + 2 < 5,7
1-c	8 ( 6x + 3) > 2x
1-d

Réponses : x "d ; x "e 1,5 ; x > ; x >

Résoudre le système suivant :

INTERDISCIPLINARITE

1°) Démontrer que la moyenne géométrique de deux nombres est toujours inférieure à la moyenne arithmétique de ces deux nombres.

2° ) Démontrer que la moyenne arithmétique de deux nombres est comprise entre ces nombres.

ACTIVITE Niveau 3^e :

(Pré requis : @ les équations du premier degré et @ les inégalités triangulaires ,et accès au corrigé)

Données :

ABC est un triangle dont les côtés ont pour mesure ( en cm).*

AB = 3x ; BC = 6 ; CA = 2x+1

Dans lequel « x » représente un nombre strictement positif.

1°) faire la figure dans le cas où « x » = 1,5

Placer [ BC ] ; puis AB = « ……… » ; CA = « …….. ».

2°) Pouvez- vous dessiner le triangle quand «x = 8 » ?

Commencer par calculer les côtés : AB = …….. ; CA = ……..

2°) Déterminer les valeurs de « x » pour lesquelles le triangle existe ( sans être aplati). Le triangle existe à condition que la longueur de chaque côté soit strictement inférieure à la somme des longueurs des deux autres côtés.

- AB < BC + CA se traduit par 3x < 6 + 2x +1 ; en transposant on obtient

3 x - 2x < 6 + 1 ; c’est à dire « x < …….»

- BC < CA + AB se traduit par 6 < …………….. ; en transposant on obtient

6 - 1< 2x + 3x ; c’est à dire « 5 < ………. »

et en divisant les deux membres par « 5 » on obtient : ……… < x

- AC < AB + BC se traduit par 2x +1 < ……………. ; en transposant on obtient

1 - 6 < ……….. ; c’est à dire « - 5 < x »

Ce qui est toujours vérifié puisque « x » est positif par hypothèse.

- En définitive le triangle existe quand 1 < x et x > 7 c’est à dire …..….. < x < ……

4°) Pour quelle valeur de « x »le périmètre du triangle est-il égal à 32 cm ?

5°) Pour quelle valeur de « x », le triangle est -il isocèle ?

- de base [ BC] ; AB = CA

- de base [ BC]

6°)

- Pour quelle valeur de « x » ; CA = 2 AB ?

- Pour quelle valeur de « x », CA = 2 BC ?

- Pour quelle valeur de « x » ; CA = AB ?

7°) Se peut -il que le double de AB soit égal au triple de AC diminué de la moitié de BC ?

Résoudre les inéquations suivantes :

1°) Résoudre l’inéquation 3x – 5 2 x + 8

2°) Résoudre l’inéquation 7x + 4 4 x + 19

3°) Résoudre l’inéquation 2x – 8 < x – 7