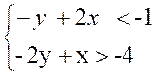|
Système d’équation
du premier degré à une inconnue |
|
|
Résolution de
l’équation du premier degré à deux
inconnues |
|
|
Fonction linéaire
(représentation graphique) |
|
|
Fonction affine
(représentation graphique) |
ENVIRONNEMENT du dossier:
|
Objectif
précédent : 1°) Inégalité
degré 1 à une inconnue |
Objectif
suivant : 1°) système de 3 ’inéquations du premier degré à deux
inconnues. 2°) suite (cours N°2) les inéquations et les systèmes
d’inéquations du premier degré à deux inconnues.. |
|
DOSSIER :
INEQUATION du PREMIER DEGRE à deux INCONNUES
et REGIONNEMENT.
II)
INEQUATIONS du Premier degré à
deux inconnues : (généralité)
Avec exemples d’application !!!!
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
Corrigé
Contrôle |
Corrigé
évaluation |
|
|
|
|
|||||||||||||||||
|
|
COURS
L’équation du premier degré à deux
inconnues a pour forme
mathématique l’égalité :
( « a » ;
« b » ; « c » Î R ) Si
« a » et « b » sont différents de zéro, cette équation
admet une infinité de solutions . La représentation graphique des solutions est une droite
.(voir
fonction affine « représentation graphique ») I ) INEQUATION du premier degré à deux inconnues :
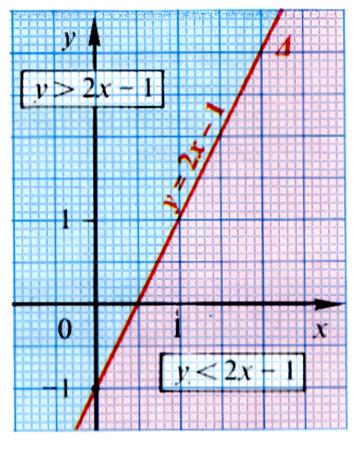
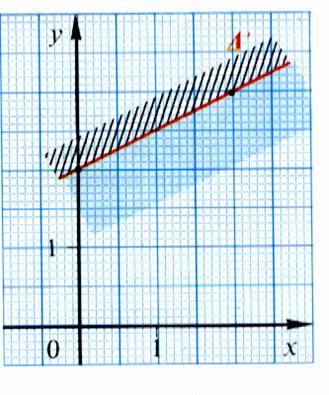
approche Exemple : Soit l’équation
y -2x + 1 = 0 Par transformation on
obtient le tracé de la droite ” d’équation y = 2x -1 . Cette droite partage le
plan en deux demi- plans.
Si y -2x + 1 = 0 (1) Soit un point A (1 ; 4)
(choisi au hasard, à la gauche de la droite ”) on remplace
ces valeurs dans l’équation (1)
Alors : 4 - 2 fois 1
+1 = 1 ; cela signifie que le
point A est dans la zone y -2x + 1
> 0 Soit un point B (2 ; 1)
(choisi au hasard, à la droite de la droite ”) on remplace
ces valeurs dans l’équation (1)
Alors : 1 - 2 fois 2 +1
= -3 ; cela signifie que le point
B est dans la zone y -2x + 1 < 0 On peut essayer de savoir si le point d’origine O (0 ;0) appartient à la zone « y -2x + 1 >
0 » ou à la zone « y -2x + 1 <
0 » en remplaçant y=0 et x=0 dans l’équation « y -2x + 1 = 0 » ; Le résultat donne « 1 » ; donc le point O appartient à
la zone « y -2x + 1 > 0 » · Remarques : 1.
Si la
droite passe par l’origine, on ‘essaie » un autre point bien choisi. 2.
Si l’inégalité est au sens large ( "d ou "e ) ,
on doit « ajouter » aux points du demi -plan les points de la
droite « frontière ». Exemple 1
d’application : On demande de résoudre l’inéquation
6 x + y – 5 Dans un premier temps : De l’inéquation précédente on en déduit l’équation : 6 x + y – 5
= 0 Dans un second temps : on écrit cette équation sous la
forme : y = m x + p Soit y = - 6 x + 5 ; on reconnaît là l’équation
d’une droite (
Cette droite ( Il
nous reste à trouver lequel des deux demi plans qui est la solution de
l’inéquation. Pour
solution : nous choisissons un
point pris dans l’un des demi-plans , relevons ses coordonnées et nous contrôlons si ce point vérifie l’inéquation . Conseil :
On choisit ,de référence, le point
« O » de coordonnées (
0 ; 0 ) ; c'est-à-dire x= 0
et y = 0 . les calculs sont donc simplifiés . ( Si la droite passe par « O » , on prendra un
autre point…) Dans l’inéquation 6 x + y – 5
Ce qui donne : 6
(0) + ( 0
) – 5
Soit – 5 Conclusion : les coordonnes
( 0 ; 0 ) ne vérifie pas l’inéquation. On généralise en concluant qu’il en est de même pour tous
les points de ce demi –plan. Ainsi on doit hachurer le demi –plan concerné. Au contraire , le
demi- plan non hachuré représente la solution de l’inéquation . Remarque : la droite ( II)
INEQUATIONS du
Premier degré à deux inconnues : GENERALITE : On appelle « inéquation du premier degré à deux inconnues
« x » et « y » l’inégalité du type : a x +by + c
> 0 ou a x + by + c <
0 Lire : a x +by + c > 0
« supérieur à 0 » Ou a x + by + c < 0 «
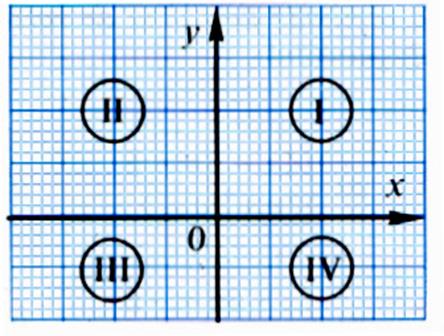
inférieur à 0 » Inéquations et demi-plan :
3°) Toute inéquation de la forme a x + by + c > 0 est associée à un demi-plan de frontière
(d) ; ( d)
exclue ; étant associée a x + by +
c = 0
d’équation y = - si c > 0 alors l’origine
« O » est dans le demi plan associée à l’équation. si c < 0 alors l’origine « O » n’ est pas dans le
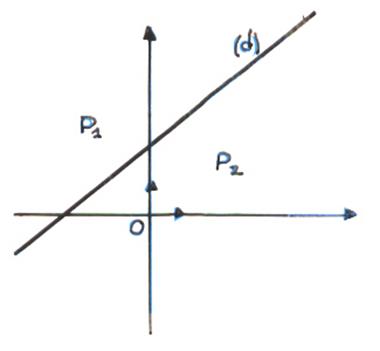
demi plan associée à l’équation. Exemple :
(d ) associée à x – 2 y
+ 3 = 0 « P1 : x – 2 y + 3 < 0 » et
« P2 : x – 2 y + 3 > 0». En
résumé : Les solutions graphiques (on dit aussi : la solution
) d’une inéquation
sont situés dans un des deux demi-plans ouverts limité par la droite d’équation « ax + by +c =0 ». L’autre demi-plan ouvert contient l’ensemble des solutions de l’inéquation
de « sens » contraire. Autre
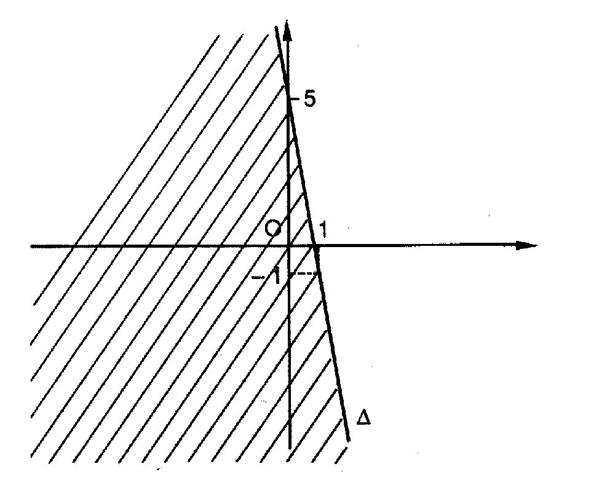
APPLICATION : Exemple :
résoudre graphiquement : x -
2y + 4 > 0 Objectif : on recherche tous les points dont les coordonnées
vérifient l’inégalité.
Applications Série 1 : 1°) Représenter graphiquement l’ensemble des solutions de chacune des
inéquations :
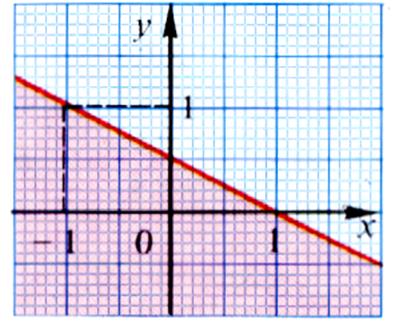
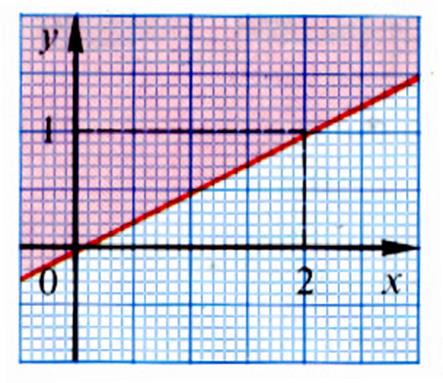
3°) Donner une inéquation dont l’ensemble des solutions correspond au
demi-plan bleu (on donnera une égalité stricte)
4°) Donner une inéquation dont l’ensemble des solutions correspond au
demi-plan rouge (on donnera une
égalité stricte)
|
|
|
|
|
|
||||||||||||||||
|
|
Travaux auto formatifs. CONTROLE : 1°)
Donner la procédure qui permet de résoudre « graphiquement » une
inéquation du premier degré à deux inconnues.
B) Résoudre le système suivant :
|
|