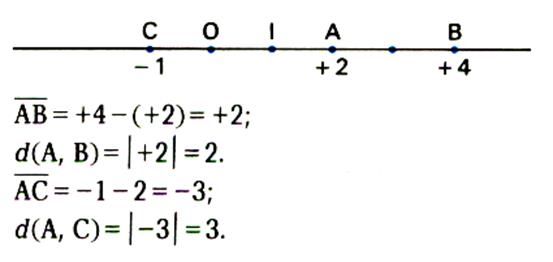Pré requis:

Les relations d’ordre

 

Droite . 3D Diamond

 

ENVIRONNEMENT du dossier:

Index warmaths  

Objectif précédent  

1°)Addition de longueur

2°)Tracé d’un triangle quelconque

Objectif suivant :

4ème  Collège : fiche 5 l’inégalité triangulaire..

Les triangles  Sphère metallique

Algèbre : les inégalités à une inconnue

Liste des cours en géométrie plane

 

 

 

 

 

 

 

 

DOSSIER : LES INEGALITES « triangulaires »

  Dont  le cas particulier

- et les prolongements :

I) Ensemble  des points équidistants de deux points donnés:

II ) Centre du cercle : ( cercle circonscrit à un triangle)

III) Expression de la distance de deux points sur une droite graduée.

IV) Distance d’un point à une droite :

V) régionnement ( ou partage ) du plan :

VI ) Inégalités et Triangles :Théorèmes :

 

TEST

           FilesOfficeverte

COURS

                FilesOfficeverte

Devoir  Contrôle FilesOfficeverte

Devoir évaluation FilesOfficeverte

Interdisciplinarité

                       Somme de vecteurs  Filescrosoft Officeverte

 

Corrigé Contrôle  FilesOfficeverte

Corrigé évaluation  FilesOfficeverte

 

 

COURS

 

Le triangle et  l’inégalité triangulaire : ( approche)

 

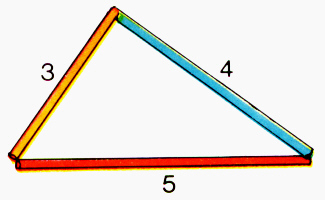
I )  Peut-on tracer un triangle avec 3 pailles mesurant :

5 cm ; 4 cm ; 3 cm ?

 

le triangle peut – être construit :

5 <  3 + 4

iné4

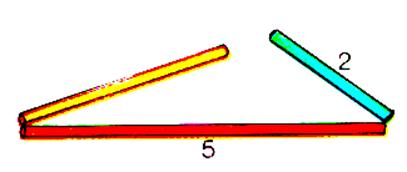
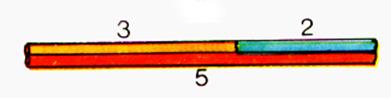
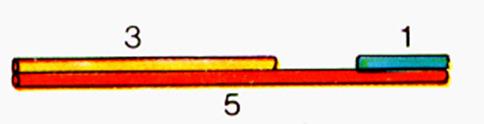
II )  Avec  3  pailles  de   5 cm ; 3cm ; 2 cm ?

Et  5 cm ; 3 cm  et 1 cm

ine3

Le triangle ne peut être construit :

5 =  3 + 2

iné2

Le triangle ne peut-être construit :

5 >  3 + 1

iné1

 

 

 

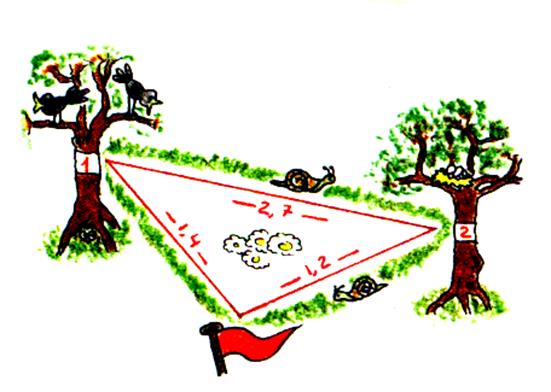
Chercher l’erreur :

 

 

Une course d’orientation est organisée dans la forêt et on a distribué aux concurrents le plan ci – contre réalisé à main levée.

Comment peut-on être sûr  que les longueurs indiqués sur ce plan sont fausses .

inetrian

 

Rappel : distance

SOS cours

On appelle distance dans un plan l’ application qui , à tout couple de points noté (A,B) du plan , associe un nombre réel positif , noté d(A,B)  ou AB

 

Remarque : le mot « distance » désigne aussi la longueur d’un segment

 

 

Inégalité triangulaire :

 

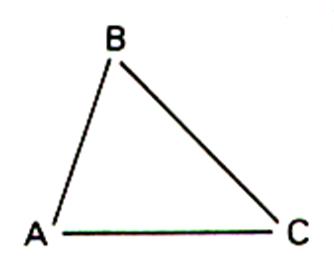
Les trois points ne sont pas alignés , il détermine un triangle.

 

inég4

Quels que soient les trois points   A,B,C du plan :

On remarque que :

 

d(A,B) £ d(A,C) +d(C,B)

 

Traduction : cette inégalité porte le nom d’inégalité triangulaire ( quand les 3 points ne sont pas alignés , ils déterminent un triangle)

 

 

 

 

 

inétri1

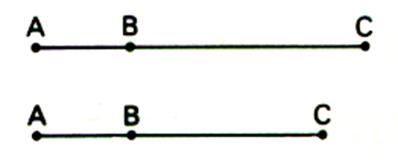
Cas particulier : les trois points sont alignés   ; dans ce cas nous avons l’égalité suivante :

inég5

 

d(A,B)  =  d(A,C) +d (C,B)

 

Cette égalité se produit dans le seul cas où « C » est un point du segment AB.

 

 

Relation de Chasles

FilesOfficeverte

 

PROLONGEMENTS :

 

I) Ensemble  des points équidistants de deux points donnés:

 

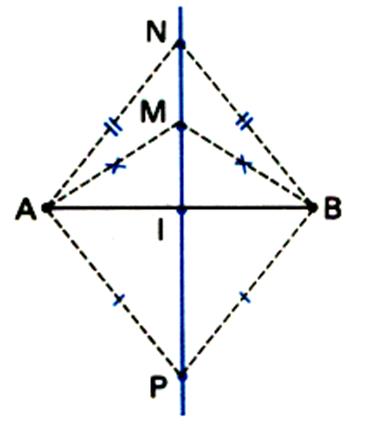
Médiatrice :L’ensemble des points équidistant de deux points A et B est une droite passant par le milieu du segment AB ; on l’appelle médiatrice de [AB]

inég7

II ) Centre du cercle : ( cercle circonscrit à un triangle)

 

 

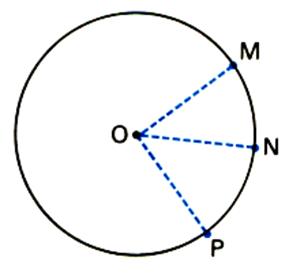
Le  cercle de centre O et de rayon R est l’ensemble des points du plan situés à la distance R du point O.

Nous disons que tous les points du cercle sont équidistant du centre du cercle.

  d(O,M) = d(O,N)= d(O,P)=R

 

inég6

 

D’où la détermination du centre du cercle :   ( voir cercle circonscrit )

cencercl1

cencercl2

 

 

 

 

III) Expression de la distance de deux points sur une droite graduée.

 

A et B étant deux points d’une droite graduée , d’abscisses respectives xA  et xB , la distance des deux points de A à B  est donnée par la formule :

 

d(A,B)=ç xB - xA ç

 

 

N.B. : les deux barres verticales se lisent « valeur absolue »

inég3

  «  » lire : mesure algébrique du bipoint AB

 

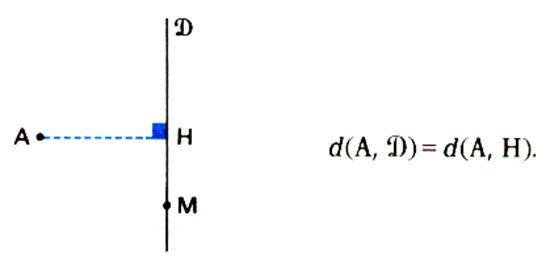
IV) Distance d’un point à une droite :

La distance du point A à la droite « D »  est la distance qui sépare le point A de son projeté orthogonal sur D

ineg2

(info ++ : niveau V)

 

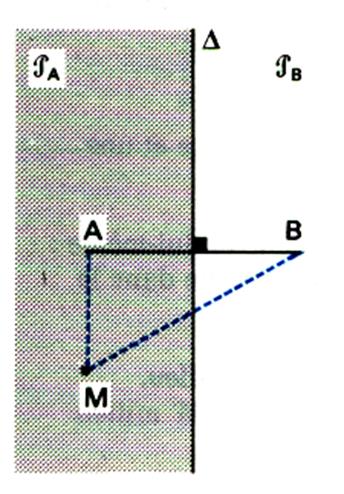
V) régionnement ( ou partage ) du plan :

 

 

Soit delta ( D) la médiatrice d’un segment AB . Delta sépare le plan en deux demi-plans PA et PB  ouverts .

Pour tout point M de PA  ,

d( M,A) < d( M,B)

 

 

( voir les systèmes d’ inégalités )

ineg1

 

VI ) Inégalités et Triangles :Théorèmes :

 

1°) Dans un triangle , au plus grand angle est opposé le plus grand côté , et réciproquement .

2°) Dans un triangle , un côté quelconque est inférieur à la somme  des deux autres et supérieur à leur différence .

 

 

 

 

TRAVAUX AUTO FORMATIFS.

 

CONTROLE :

 

Quand y a-t-il inégalité triangulaire   ?

Dans quel cas l’inégalité n’existe pas ?

 

EVALUATION

 

1°)Tracer trois points : B D et F dans un plan ; montrer l’inégalité triangulaire.

2°)Tracer trois points : G , H  P dans un plan ; montrer par le tracé l’égalité triangulaire.

3°) Dans  chaque ligne du tableau ci dessous  , on donne la mesure en cm de 3 segments . Comparer la longueur du plus grand segment à la somme des longueurs des deux autres . Ecrire « oui » dans la dernière colonne si ‘on peut construire le triangle avec les 3 segments  , « non » dans le cas contraire .

 

Mesure des segments

comparaison

Le triangle existe – t- il ?

11

15

8

15  <  11 + 8

Oui

 

23

16

12

 

 

 

5

4

14

 

 

 

18

20

32

 

 

 

40

25

15

 

 

 

43

50

26

 

 

 

 

 

INTERDISCIPLINARITE

 

Voir la somme des vecteurs : analyse ;  ( pré requis : @le premier degré équation et    @  inéquation)

ACTIVITE : niveau 3e 

Données : 

ABC est un triangle dont les côtés ont  pour mesure ( en cm).*

AB = 3x ; BC = 6 ; CA =  2x+1

Dans lequel « x » représente un nombre strictement positif.

 

1°)  faire la figure dans le cas où « x » = 1,5

 Placer [ BC ] ; puis AB =  « …….. » ; CA = « ……… ».  

2°) Pouvez- vous dessiner le triangle quand «x = 8 » ?

 

Commencer par calculer les  côtés : AB =  ………. ; CA = …………

 

2°) Déterminer les valeurs de « x » pour lesquelles le triangle existe ( sans être aplati). Le triangle existe à condition que la longueur de chaque côté soit strictement inférieure à la somme des longueurs des deux autres côtés.

 

 - AB < BC + CA   se traduit par   3x < 6 + 2x +1 ; en transposant on obtient

               3 x - 2x < 6 + 1 ; c’est à dire   «   x <  …… »   

 

- BC <CA + AB   se traduit par   6 <  …………….   ; en transposant on obtient

               6 - 1< 2x + 3x  ; c’est à dire   «   5 <  ……. »   

et en divisant les deux membres par « 5 » on obtient :        ………. <  x

 

- AC < AB + BC    se traduit par   2x +1 <  ………………   ; en transposant on obtient

               1 - 6 <   …………..  ; c’est à dire   «   - 5 < x »   

Ce qui est toujours vérifié puisque « x » est positif par hypothèse.

-       En définitive le triangle existe quand  1 < x et x > 7 c’est à dire  ……. < x < ……..

 

4°) Pour quelle valeur de « x »le périmètre du triangle est-il égal à 32 cm ?

 

5°) Pour quelle valeur de « x », le triangle est -il isocèle ?

 

- de base [ BC]    ;    AB = CA

 

- de base [ CA]     ;   

 

- de base [ BC]      

 

6°)

- Pour quelle valeur de « x » ; CA = 2 AB ? 

 

-       Pour quelle valeur de « x », CA = 2 BC ?

 

-       Pour quelle valeur de « x » ; CA =  AB ?

7°) Se peut -il que le double de AB  soit égal au triple de AC diminué de la moitié de BC ?

 

 

 

 

 

 

CORRIGE du problème :

ACTIVITE : (discipline «  géométrie » : @ les inégalités triangulaires)

 

Données : 

ABC est un triangle dont les côtés ont  pour mesure ( en cm).*

AB = 3x ; BC = 6 ; CA =  2x+1

Dans lequel « x » représente un nombre strictement positif.

 

1°)  faire la figure dans le cas où « x » = 1,5

 Placer [ BC ] ; puis AB =  « 4,5 » ; CA = « 4 ». 

2°) Pouvez- vous dessiner le triangle quand «x = 8 » ?

 

Commencer par calculer les  côtés : AB =  24 ; CA = 17

24 >  17 + 6   Un côté est supérieur à la somme des deux autres. Le triangle n’existe pas.

 

2°) Déterminer les valeurs de « x » pour lesquelles le triangle existe ( sans être aplati). Le triangle existe à condition que la longueur de chaque côté soit strictement inférieure à la somme des longueurs des deux autres côtés.

 

 - AB < BC + CA   se traduit par   3x < 6 + 2x +1 ; en transposant on obtient

               3 x - 2x < 6 + 1 ; c’est à dire   «   x <  7 »   

 

- BC <CA + AB   se traduit par   6 <  2x +1 + 3x   ; en transposant on obtient

               6 - 1< 2x + 3x  ; c’est à dire   «   5 <  5x »   

et en divisant les deux membres par « 5 » on obtient :        1 <  x

 

- AC < AB + BC    se traduit par   2x +1 <  3x + 6   ; en transposant on obtient

               1 - 6 <   3x - 2x  ; c’est à dire   «   - 5 < x »   

 

Ce qui est toujours vérifié puisque « x » est positif par hypothèse.

-       En définitive le triangle existe quand  1 < x et x > 7 c’est à dire  1 < x < 7

4°) Pour quelle valeur de « x »le périmètre du triangle est-il égal à 32 cm ?

On doit avoir : 2x + 1 + 3x + 6 = 32 , on regroupe dans le premier membre    2x + 1 +3x + 6 - 32 = 0 ; après réduction, on obtient : 5x - 25 = 0 d’où  x = 5

 

5°) Pour quelle valeur de « x », le triangle est -il isocèle ?

 

- de base [ BC]    ;    AB = CA

réponse :  3x = 2x + 1 , c’est à dire 3 x - 2 x - 1 = 0 d’où  x = 1  mais dans ce cas , AB = 3 et CA = 3 ; BC = 6 le triangle est aplati.

- de base [ CA]     ;    AB = BC

3x = 6 d’où x = 2 le triangle existe car 1 < 2 < 7

 

- de base [ BC]       AB = CA   ;  6  =  2x + 1 c’est à dire 5 = 2x d ‘ où  x = 2,5

le triangle existe car 1 < 2,5 < 7

 

6°)

- Pour quelle valeur de « x » ; CA = 2 AB ?  On doit avoir 2x + 1 = 6x

 

c’est à dire 1 = 4 x d’où x = 1/4 qui ne convient pas car  1/4 < 1

 

- Pour quelle valeur de « x », CA = 2 BC ? On doit avoir 2x + 1 = 12 c’est à dire 2x = 11 d’où x = 5,5 qui convient car   1 <5,5 <7

 

-       Pour quelle valeur de « x » ; CA =  AB ? On doit avoir 2x + 1 = × 3 x  c’est à dire 2x + 1 = 2x  Après simplification  il reste  1 = 0 . Pas de solution

7°) Se peut -il que le double de AB  soit égal au triple de AC diminué de la moitié de BC ? On doit avoir 6x = 3 ( 2x + 1) - 3 c’est à dire 6x = 6x + 3 - 3 Après simplification, il reste 0x = 0. C’est toujours vrai quel que soit « x ».

 

 

 

 

 

y:Arial'>Voir la somme des vecteurs : analyse