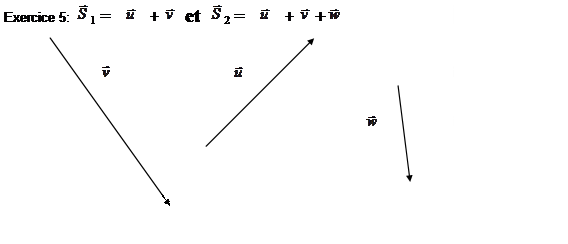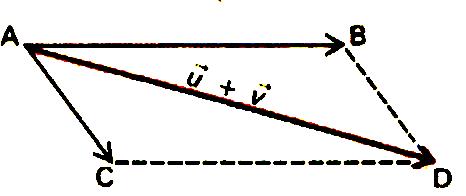|
|
|
|
|
|
|
Pré requis: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : IMPORTANT : si vous avez des problèmes , il faut
reprendre à ce niveau : voir la
définition d’un BIPOINT suivi du « bipoint équipollent » |
Objectif suivant : |
Info
générales : |
|
|
Objectif suivant |
|
|
Module : LES
VECTEURS DOSSIER LA SOMME DE DEUX VECTEURS "non colinéaires" |
|
|
|
|
|
|
|
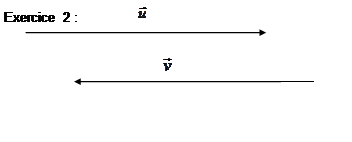
- Cas particuliers : les vecteurs colinéaires |
|
|
|
3°) Propriétés : : Propriétés de
la somme de vecteurs |
|
|
|
|
|
|
|
|
|
|
|
Quel que soit le vecteur |
|
|
|
|
|
|
TEST |
COURS |
Interdisciplinarité |
|
Corrigé Contrôle |
|
|
COURS |
|
||||
|
|
|
|
||||
|
|
1°)LA SOMME
GRAPHIQUE de deux VECTEURS : |
|
||||
|
|
|
|
||||
|
|
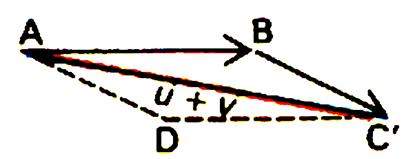
Construction du vecteur somme : Le vecteur AD
est le « vecteur somme » Est obtenu avec : Tel que le
quadrilatère : ( A,B,C,D) soit
un parallélogramme. |
|
|
|||
|
|
Dans le cas précédent on aurait pu écrire
que : |
|
||||
|
|
Cas particulier : |
|
|
|||
|
|
On peut écrire que Ce genre d’égalité est connue sous le nom de
« relation de
Châles ». Cette relation
permet de résoudre des
exercices du type : Ecrire plus simplement :
2°) 3°) on sait que
4°) |
|
|
|||
|
|
|
|
||||
|
|
Remarque : Sciences , en statique , le
vecteur somme est appelé « résultante » des forces. Ainsi |
|
|
|||
|
|
|
|
||||
|
|
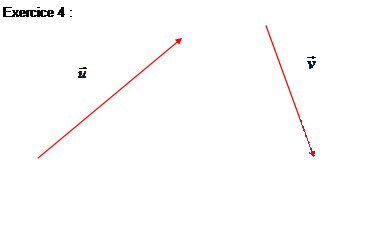
Activités : Tracer le bipoint noté ( A,B) représentant
de : . Tracer le bipoint noté (A’,B’) représentant de : |
Dessin 1 |
|
|||
|
|
Que
peut - on dire des bipoints (A,C) et (A’,C’ ) ? r réponse : ces bipoints sont des représentants du vecteur ,noté : |
|
||||
|
|
La somme |
|
||||
|
|
|
|
||||
|
|
Nous pouvons écrire sous forme
mathématique : |
|
||||
|
|
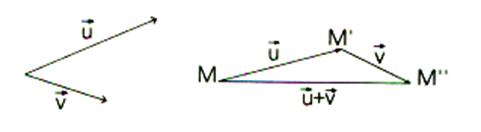
Traduction : appliqué aux vecteurs : CAS GENERAL : (vecteurs non colinéaires ou colinéaires) Représentation graphique du vecteur « somme » ; nommé :
|
Dessin 2 |
|
|||
|
|
Procédure de traçage : - fixer
(sur le plan feuille ) la position du premier point (A’)origine du premier bipoint. - tracer le vecteur AB ; (( A’,B’
)bipoint équipollent AB) , on peut dire « faire glisser par translation
le vecteur AB en A’ » -
translater le vecteur DC ,
(L’extrémité du premier vecteur
coïncide avec l ‘origine du deuxième vecteur) -
Joindre l’origine du premier
vecteur avec l extrémité du second
vecteur ;
le vecteur
« somme » noté Remarque : le
vecteur |
|
||||
|
|
Complément :
Somme de deux vecteurs . |
|
||||
|
|
|
|
||||
|
|
|
|
||||
|
|
CAS PARTICULIER: somme de deux vecteurs perpendiculaires, |
|
||||
|
|
|
Dessin 3 |
|
|||
|
|
|
|
||||
|
|
|
|
||||
|
|
D' après la relation de CHASLES nous pouvons écrire que
La construction de la
somme est toujours possible. |
Dessin4 |
|
|||
|
|
« norme d’un
vecteur » En général , la norme ( certains diront la longueur ou mesure )
du vecteur somme est différente de la somme des normes des deux
vecteurs : ce qui se traduit en écriture mathématique :
|
|
||||
|
|
Voir dans
les exercices suivants , le cas particulier où : |
|
||||
|
|
2°) CALCUL Somme de vecteurs
|
|
||||
|
|
Soit deux vecteurs |
|
||||
|
|
|
|
||||
|
|
Exemple :
on nous donne : |
|
||||
|
|
On applique : |
|
||||
|
|
Soit |
|
||||
|
|
|
|
||||
|
|
Cas particuliers : les vecteurs colinéaires |
( INFO PLUS : sur
la somme graphique de vecteurs
colinéaires ;cliquer ici ) |
|
|||
|
|
|
|
||||
|
|
« colinéaires » Les
vecteurs « colinéaires » ont la même direction ( pas forcément le même sens , la même
norme .) |
Dessin 5 |
|
|||
|
|
soit un vecteur le vecteur « Dit autrement : Des vecteurs colinéaires sont des vecteurs qui ont des
supports parallèles, (ou superposés)
indépendamment du sens et de la norme de ces vecteurs |
|
||||
|
|
|
|
||||
|
|
VECTEURS EQUIPOLLENTS : |
|
||||
|
|
Deux vecteurs sont équipollents si il ont la même
norme , le même sens , et dont les supports sont parallèles (ils donc aussi
« colinéaires ») Ils forment un parallélogramme: |
Dessin6 |
|
|||
|
|
|
|
||||
|
|
3°) Propriétés de la somme de vecteurs |
|
|
|||
|
|
|
|
||||
|
|
a) LA COMMUTATIVITE |
|
||||
|
|
-
On vous donne un point A . -
Tracer le bipoint (A,B) représentant de -
Tracer le bipoint (A,D) représentant de Que peut - on dire des points C et E ? Que peut - on dire des bipoints ( A,C) et ( A,E) ? La somme de deux vecteurs est indépendante de
l’ordre dans lequel on effectue cette somme :
( cette propriété s’appelle la
commutativité) |
Dessin 7 |
|
|||
|
|
b) ASSOCIATIVITE : |
|
||||
|
|
Quels que soient les vecteurs :
|
|
||||
|
|
|
|
|
|
|
|
|
|
c) Elément neutre |
|
|
|
Quel que soit le vecteur on dit que
le vecteur nul Pour tout vecteur |
|
|
|
4°) Somme de 3 vecteurs : |
|
|
|
Dessin 8 |
|
|
|
Tracer le
bipoint (A,B) représentant de Tracer le bipoint (C,D)
représentant de Que peut - on dire des points D et G ? Que peut - on dire des bipoints ( A,D) et ( A , G ) ? Si (cette propriété
s’appelle : l ’
ASSOCIATIVITE ) |
|
|
|
|
|
|
|
5°)L’OPPOSE du vecteur ( cliquer ici :
information plus sur l’opposé d’un vecteur) |
|
|
|
Activité : tracer le bipoint ( A, B) représentant de Que peut - on dire des points A et
C ?.........................................du bipoint ( A ,C )............... Quelque soit
le vecteur
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Travaux auto formatifs
CONTROLE :
1°) Traduire en langage littéral : ![]() =
= ![]() +
+ ![]()
2°) Traduire en langage littéral :
![]()
![]()
![]()
(faire les exercices page : ............)
3°) Il est un cas
où ![]() =
= ![]()
Donner sa
représentation graphique ; citer les deux conditions nécessaires.
4° ) Donner la procédure permettant de tracer la somme de deux vecteurs (dispersés dans un plan )
5°) Quels sont les caractéristiques du vecteur somme ( noté : ![]() ). ?
). ?
6°) Quels sont les trois principales
propriétés de la somme de deux vecteurs
(ou trois vecteurs) ?
(donner pour chaque le modèle mathématique )
7 ° ) Quelles sont les caractéristiques du « vecteur opposé » à un vecteur
donné ? (donner un exemple graphique)
8°) Quand dit - on que deux ( ou plusieurs) vecteurs sont colinéaires ?
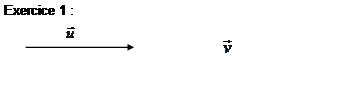
EVALUATION :
tracer ![]() =
= ![]() +
+ ![]()
![]()