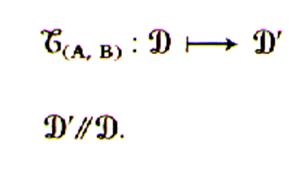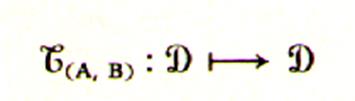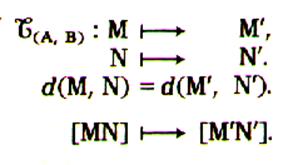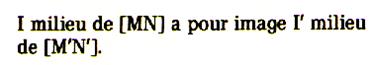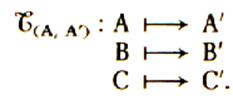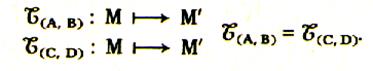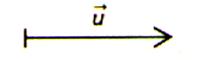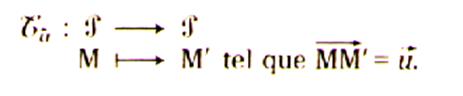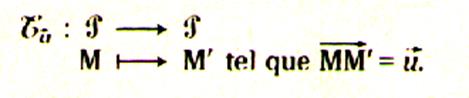Pré
requis:
|
|
|
|
Vocabulaire : BIPOINTS: |
|
|
|
|
|
|
|
|
direction |
Environnement du dossier:
|
Objectif précédent |
Objectif suivant : |
Tableau |
DOSSIER : LES
TRANSLATIONS
1.
-Bipoint
référent
2.
-Définition
3.
-Propriétés
|
TEST |
COURS 4e |
Interdisciplinarité |
|
Pour effectuer une translation nous avons besoin
d’un « bipoint de référence »afin de connaître le sens et la
direction de cette translation)
|
Soit un bipoint du plan. (noté : (A,B) ) ( vocabulaire :
« BIPOINT ») |
|
|
Ainsi dans la pratique il faut savoir que tous les points donnés se
déplaceront en translation en suivant
une parallèle à la
droite support du bipoint
« fixé » en référence. |
|
2°) DEFINITION : «
translation »
3°) Propriétés de la translation :
|
1 ) L’image d’un point dans une translation est un autre point dont: - la distance entre les deux points est imposée - la
direction de déplacement est imposée par le bipoint référent
. |
|
|
M’ est l’image de M par translation par rapport au bipoint de référent
A,B (direction donnée par le support
du bipoint AB) |
|
|
Bipoint référent |
|
|
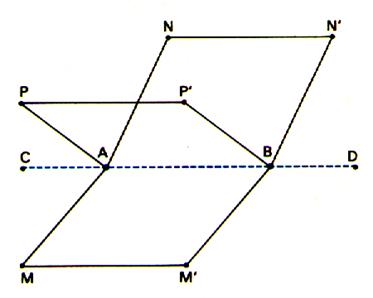
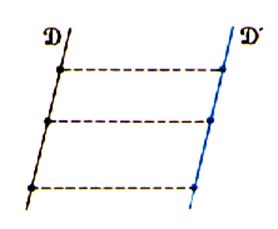
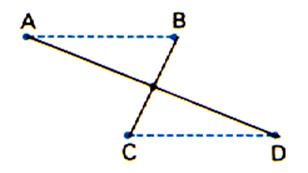
2 ) L’image d’une droite dans une
translation est une autre droite parallèle à la première. L’image de « D » dans
une translation est une droite
« D’ » parallèle à
« D » ; la translation
n’est possible que si l’on a ,au préalable , donné
un bipoint référent. |
|
|
Ce qui se traduit , en écriture
mathématique : |
|
Bipoint
référent
|
|
|
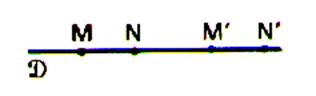
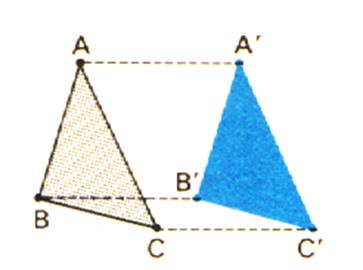
Une translation conserve les
distances. En effet si l’on découpe une figure géométrique on trace le contour
sur une feuille , ensuite on fait glisser la figure
suivant une direction donnée (translation) , on trace le contour de la figure
(que l’on nomme « translation » ) , on constate que nous avons la
même « reprographie » . |
|
|
Ce qui se traduit , en écriture
mathématique : L’image d’un segment est un segment |
|
|
|
|
Une
translation conserve le milieu
|
|
Bipoint
référent
|
|
|
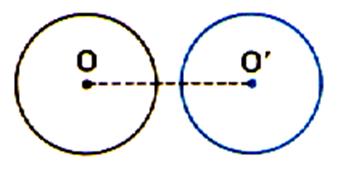
L’image d’un cercle est un cercle de même rayon |
|
Bipoint référent
|
|
|
A partir des propriétés précédentes : L’image d’une figure est une figure de même type et de mêmes dimensions , par
conséquent :de même aire. Notation :
|
Exemple :
|
Egalité de deux translations
Bipoint
référent
|
|
|
|
|
|
Ce qui se traduit : |
|
4°) Relation entre : Translation et vecteur
Soit la
translation du point M
|
|
|
on peut associer à ce vecteur une translation
unique : On l’appelle translation de vecteur |
|
|
Notation : |
|
|
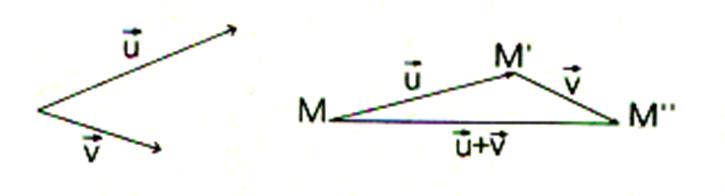
Application : translation de
deux vecteurs : Voir la somme de deux vecteurs est obtenue en
faisant une translation du vecteur « v ». Le vecteur d’origine M et d’extrémité M’’ est
appelé le « vecteur somme » |
|
|
|
|
TRAVAUX AUTO FORMATIFS.
1°) Définition d’une translation :
2°) Comment note –t-
on : translation de bipoint A,B ?
3°) Citer les
propriétés d’une translation. :
les propriétés d’une translation sont :
4° ) Traduire l’écriture suivante :
|
|
5°) Quand a-t-on égalité de deux translations :
EVALUATION :
|
Tracer deux vecteur s |
|