Pré requis:

Savoir tracer un parallélogramme : 1°)  à la règle et au rapporteur ; 2°) à la règle et l’équerre , 3°) avec un compas et une règle.
·      Le parallélogramme  tracés recherche du quatrième point
·      Point

Environnement du cours :

Index : warmaths	Objectif précédent : Le bipoint	Objectif suivant : 1°) La translation de vecteur ( 3ème ) 2°) Le vecteur	tableau      2°) Vecteur : présentation des objectifs.

 

Les leçons sur  Le bipoint et le bipoint équipollent  sont très importanteselles vont permettent de  comprendre la définition et la représentation d’un vecteur .

 

 

 

 

	Le Bipoint équipollent.
	1°) Définition  de « bipoint équipollent » :
	2 ° )  Ensemble de bipoints équipollents .et « vecteurs »
	3°)   Notion de vecteur .
	4°) ACTIVITES   COURS

 

 

TEST	COURS	Devoir  Contrôle	Devoir évaluation	Interdisciplinarité		► Corrigé Contrôle Et évaluation
	résumé	Travaux devoir
						Devoir formatif.	Devoir auto formatif  @ :

 

 L’objectif précédent « définition d’un bipoint » et cet objectif  est important, il  permet de donner à comprendre la définition du « vecteur » :

 

Définition « géométrique »  du vecteur  qu’il faudra connaître au prochain objectif:

On appelle « vecteur » l’ensemble des bipoints équipollents à un bipoint donné.

 

	DOSSIER :  LES VECTEURS
N°2	Leçon : LE BIPOINT EQUIPOLLENT

 

 

 

 

	COURS :
	Forme générale de la : 1°)  Définition  de « bipoint équipollent » :
	Un bipoint  noté ( O2 , E2 )  est équipollent à un bipoint donné ( O1 , E1 ) si le segment  de droite reliant l’origine  ( O 1) du premier bipoint  et l’extrémité du second bipoint (E2 )   et le segment de droite  reliant l’extrémité du premier bipoint ( E1) et l ’ origine du second bipoint (O2) se coupent en leur milieu. (propriété déjà vu :r les diagonales d’un parallélogramme)
	Le  Symbole   :       ~    il faut  lire « équipollent »

 

 

 

 

 

 

 

 

 

 

 

 

 

Ecriture :

  

 

 

 

 

 

 

 

 

 

 

 

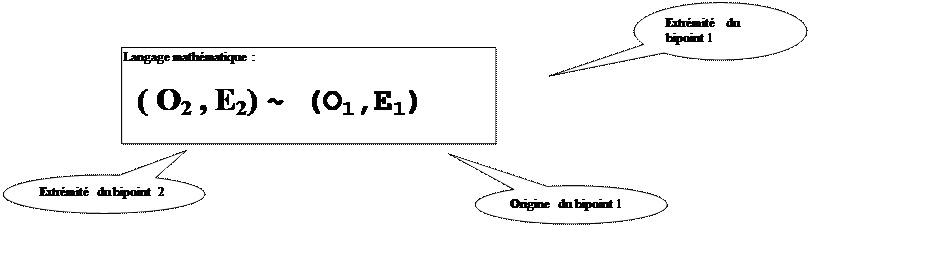
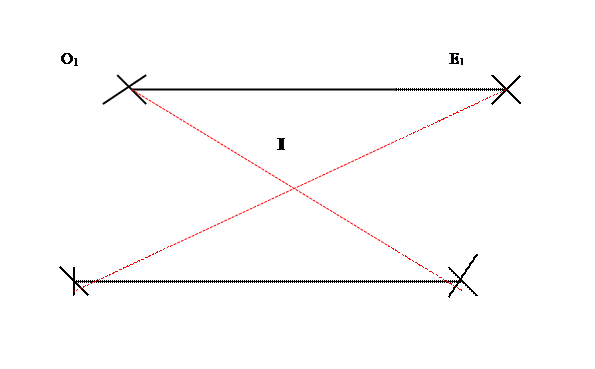
                                            Représentation graphique :Tracé :

 

 

 

		O2
						E2

 

 

 

 

 

 

 

 

 

 

 

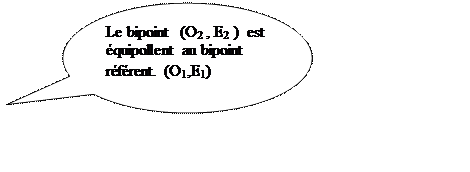
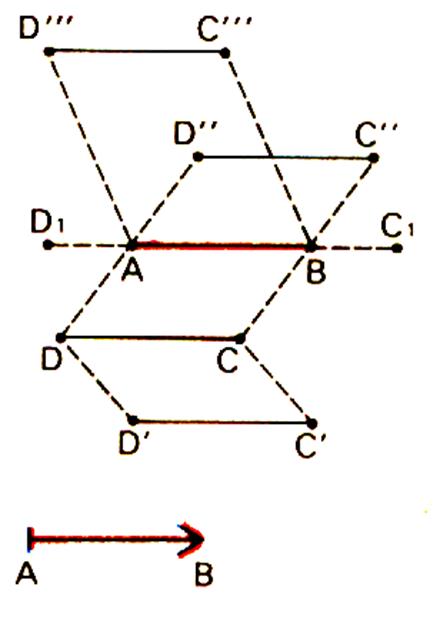
REMARQUE :  Les quatre points de deux bipoints équipollents  forment  les sommets d’un parallélogramme . ( dans   un parallélogramme  les diagonales se coupent en leur milieu.)

Application :     Le bipoint AB , noté : (A, B)  est équipollent au bipoint CD , noté : (C,D) si les bipoints (A,D) et (B,C) ont  le  même milieu .

 

Alors on notera :                             ( A,B)  ~ (C,D)   ,

on lira :   le bipoint (A,B) est équipollent au bipoint (C,D) 

Activité : dans un plan on a placé trois points « A » ; « D » et « C » .

			Consignes : Placer  le milieu du bipoint (A,D). Placer le point B tel que  I soit le milieu du bipoint (B,C)

 

 

 

 

 

 

 

 

 

 

 

 

Remarques :

Si  les points « A » , « B » , « C » , « D »  ne sont pas alignés  et si  le quadrilatère (A , B , D , C ) à ses diagonales qui se coupent en leur milieu , c'est un parallélogramme .

(attention lire les points du quadrilatère (A , B ,  D, C  ) dans le sens des aiguilles d'une montre)

 

Si (A,B) est équipollent à ( C,D) alors  (C,D) est équipollent à (A,B).

Si (A,C) est équipollent à ( B,D) alors  (B,D) est équipollent à (A,C)

 

(A,B) est équipollent à (A,B).

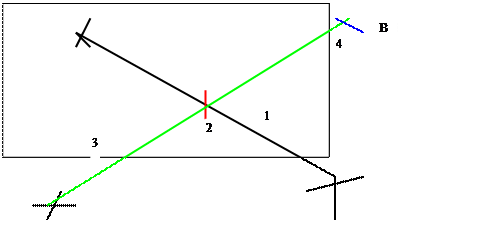
			Tracer dans l’ordre : 1 ; 2 ; 3 ; 4 ;

 

 

 

2°   )  Ensemble de bipoints équipollents .et « vecteurs »
Il y a une infinité de bipoints ( C,D) formant  avec le bipoint ( A,B )  un parallélogramme ( A, B , C , D ) Remarque : si A,B,C,D sont des points alignés ( A,B,C,D) est un parallélogramme aplati..
3°) Notion de vecteur :
Un bipoint ( A,B) étant donné , on appelle « vecteur AB »  l’ensemble de tous les bipoints  (« D »,  « C ») du plan  tels que  le quadrilatère ( A, B , C , D ) soit un parallélogramme. Pour faire exister ce vecteur  on le représentera par un segment de droite « orienté » , c’est à dire « fléché »  (  INFO plus : le vecteur )

 

 

4°) ACTIVITES   COURS

 

Exercice 1: Construire le bipoint (Q,R) équipollent au bipoint ( S,T)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

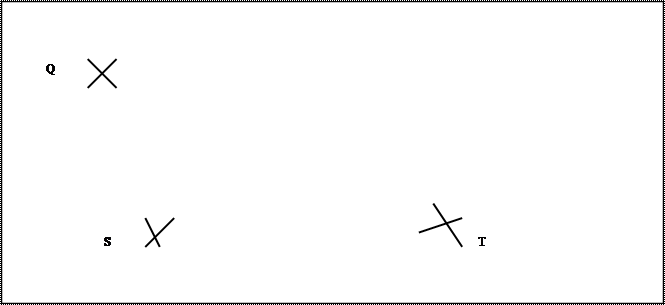
Exercice 2 : Construire le bipoint  ( A,B) équipollent au bipoint ( C,D)

 

 

 

 

 

 

 

 

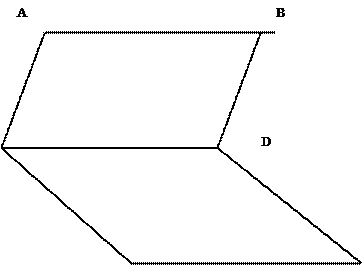
Exercice 3 :

(A,B) et (C,D)  sont équipollents ; (C,D) et (E,F)

sont équipollents. Quel est la nature du quadrilatère (A,B,D,C) ?

Que peut - on dire des segments [ AB] et [CD ] ?

 

Quelle est la nature du quadrilatère ( C,D,F,E ) ?

Que peut - on dire des segments [ EF] et [CD ] ?

En déduire la nature du quadrilatère ( A,B,F,E )

Que peut - on dire des bipoints  (A,F) et E,B) ?

Que peut - on dire des bipoints ( A,B ) et (E,F) ?

	C
							F
				E

 

 

 

 

 

 

 

 

 

 

 

 

 

EXERCICES   COURS CORRIGES

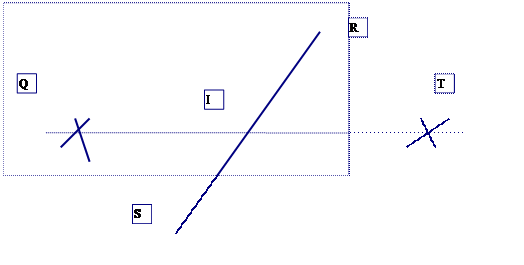
Corrigé Exercice 1: Construire le bipoint (Q,R) équipollent au bipoint ( S,T)

 

			IL faut construire le parallélogramme :Q,R,T,S La droite passant par QT étant la diagonales de ce parallélogramme.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

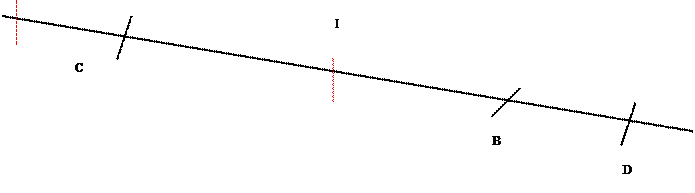
Exercice 2 : Construire le bipoint  ( A,B) équipollent au bipoint ( C,D) ; Il faut construire le parallélogramme (plat ) , ou AD et BC sont les diagonales du parallélogramme.

Tracer I milieu de la diagonale  « existante » BC ; et ensuite tracer au compas le point A

 

 

 

 

 

 

 

 

 

 

 

 

 

Exercice 3 :

(A,B) et (C,D)  sont équipollents ; (C,D) et (E,F)

sont équipollents. Quel est la nature du quadrilatère (A,B,D,C) ? Parallélogramme

Que peut - on dire des segments [ AB] et [CD ] ?

ils sont se coupent en leur milieu

Quelle est la nature du quadrilatère ( C,D,F,E ) ?

Parallélogramme

Que peut - on dire des segments [ EF] et [CD ] ?

ils sont se coupent en leur milieu

En déduire la nature du quadrilatère ( A,B,F,E ) : Parallélogramme

 

Que peut - on dire des bipoints  (A,F) et E,B) ? ils sont équipollents

Que peut - on dire des bipoints ( A,B ) et (E,F) ? ils sont équipollents

 

 

 

 

 

 

 

 

	TRAVAUX AUTO FORMATIFS.
	CONTROLE:   1°)Tracer un parallélogramme quelconque, et donnez ses caractéristiques.     2°) Donnez la définition littérale d'un "bipoint équipollent  à un bipoint donné".(forme générale).   3°) Donnez le modèle symbolique mathématique traduisant l'écriture littérale "bipoint équipollent à un bipoint donné"   4°) Donnez la représentation graphique (dessin ou schéma)d'un bipoint équipollent à un bipoint donné.   5°) Traduire en langage littéral:          (F,G)    ~   (M,N)   6°) Dans un plan,(compléter la phrase):       4 points non alignés d'un quadrilatère représente un parallélogramme si ....................
	EVALUATION:    1°) A l'aide d'une règle graduée et d'un compas ,tracer un parallélogramme.(2 cotés lg = 4 cm;2 autres >6 cm)        et   Nommez les points.    2°) Donnez ses caractéristiques.      Rappel :le sens de lecture des notations des points est très important,(éventuellement demander des précisions)   3°) A partir de trois points distincts construire un parallélogramme.(indiquer le point "I", milieu des diagonales)   4°) Soit un bipoint A à B;        tracez un bipoint équipollent C à D à ce bipoint ;noté (A,B)   5°) Soit un parallélogramme BCDE établir toutes les relations d'équipollence existant entre les bipoints.   6°)Soit un bipoint donné ,tracer un bipoint équipollent au bipoint " (B,A) ".                               + B                         A +     7°) Tracer un bipoint à (B,D) ,départ en "F"                                        +D                       B +                                            +                                               F

 

	DEVOIR sommatif (à donner à tous les élèves )   I  ) donner la définition de l’équipollence d’un bipoint :      I I )    Traduire en langage littéral :      ( O2 , E2)  ~ (O1,E1)     II I ) Donner la représentation graphique de cette équipollence :                          (à quelles connaissances et à quelle  figure géométrique  faisons nous appelle)