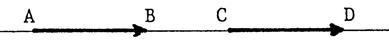Classe de 3^ème collège.
Programme 3^ème .
	Allez vers le corrigé …

Pré requis:

Point : Pré requis : ce qu’est un point..................)
Revoir le cours sur l’addition de deux nombres relatifs@…

ENVIRONNEMENT du dossier:

Index : warmaths

Objectif précédent : - Plan , ligne , point : généralités - Voir : cours de 4^ème

Objectif suivant : 1°) Le bipoint équipollent 2°) mesure algébrique d'un bipoint sur une droite. 3°) Vers le cours sur « translation et vecteur » 4°) Composition de translation et « somme de deux vecteurs »)

1°) Vecteur : présentation des objectifs.

Fiches 3^ème : La translation de vecteurs

Fiche 1 : Prérequis :

rappel : Translation.

Fiche 2 : Vecteurs égaux et parallélogramme.

Fiche 3 : Milieu d’un segment.

Fiche 4 : Situation problème.

Fiche 5 : Translation et coordonnées.

(voir suite : les coordonnées appliquées aux vecteurs )

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Fiche 1 : on revoit les Prérequis : voir en classe de 4^ème								Translation et vecteurs.
Rappels :  « Translation » et «translation d’un vecteur » :
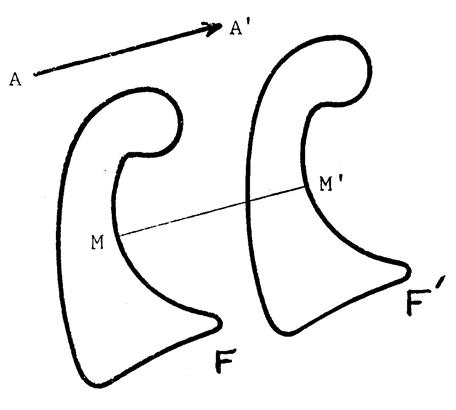
Le dessin ci-contre illustre le fait que «  F’ » et l’image de « F » dans la translation de vecteurs : · Pour comprendre cette situation , imaginez que l’on a déplacé en bloc « F » pour l’amener sur « F’ » de telle sorte que ce déplacement se fasse :
Dans cette translation, tout point « M » de « F » a pour image « M’ » de « F’ » tel que :
	- (MM’) a la direction de (AA’) c'est-à-dire (MM’) est ………………….. à ( AA’)
	- Le sens de « M » vers « M’ » est le même que le sens de « ….. » vers « ……. »
	- Les longueurs « MM’ » et « AA’ » sont ……………..
-
- Cette direction
- Ce sens		Caractérisent le vecteur de la translation.
- Cette longueur
Le vecteur définit la même translation des  ; on écrit alors :
A retenir :
			( AA’) et ( MM’) ont même ………………… , c'est-à-dire ( AA’) // ( MM’)
signifie			Le sens de « A » vers « A’ » est le même que le sens de « ….. » vers « …… »
			Les longueurs « AA’ » et « MM’ » sont …………………..
Dessin représentant un vecteur :
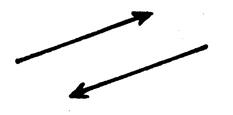
Pour représenter graphiquement un vecteur, on dessine un segment fléché.
Exemple : ( voir ci-contre) La droite (TS) donne la …………… du vecteur . La flèche indique le ………….. du vecteur. « T » est l’origine et « S » l’extrémité du couple ( T , S ) ( appelé : bipoint) La longueur de donne la ……………… du vecteur.
Nota : il y a une infinité de couples de points correspondant au même vecteur. Il y a donc une infinité de façons de représenter un vecteur. (voir ci-contre)
Notation : On a désigné par le vecteur correspondant au couple de points noté ( M , M’ ) ; mais on peut désigner un vecteur par une seule lettre , par exemple :  ;  ; …. ; etc. ………. Dire que « B’ » est l’image de « B » dans la translation de vecteur  ; c’est dire que : ……………..= ……………….
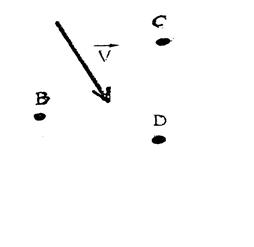
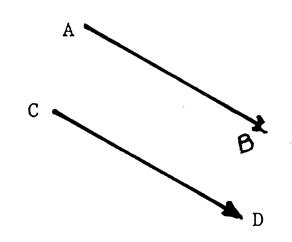
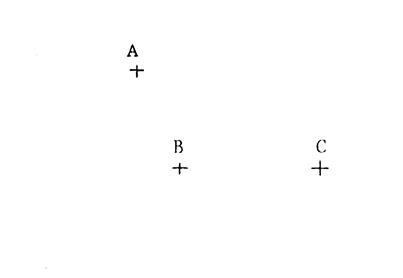
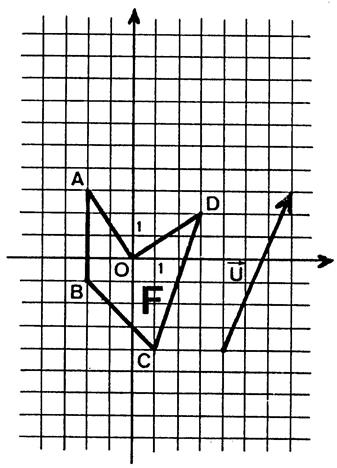
Activité 1 : Dessinez « B’ » ; « C’ » ; « D’ » des points « B » , « C » , « D » dans la translation de vecteur  .
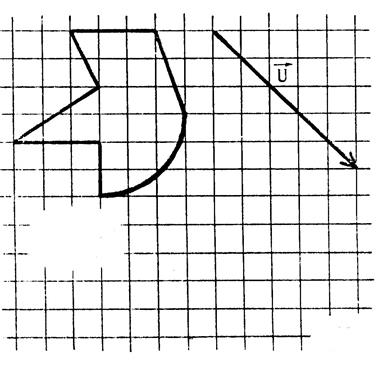
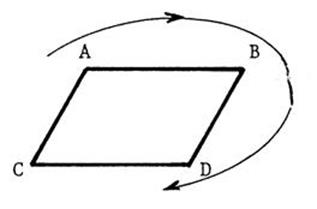
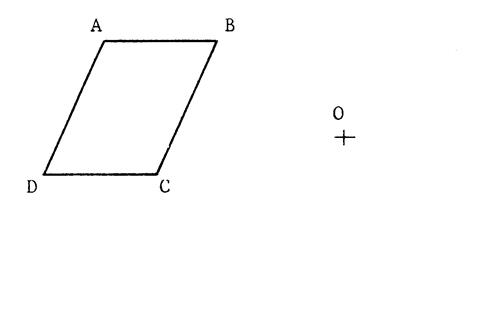
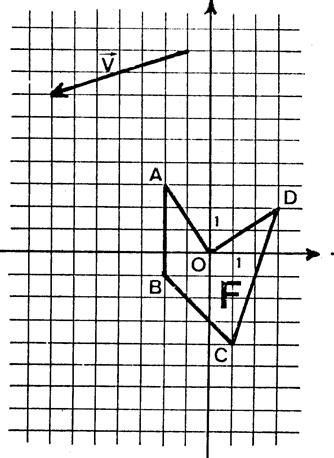
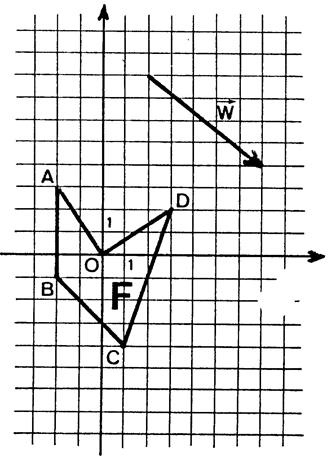
Activité 2 : Dessinez l’image de la figure ci-contre dans la translation de vecteur .

Fiche 2 : Vecteurs égaux et parallélogramme.				Info ++@...
« A » , « B » , « C » , « D » sont quatre points non alignés . Considérons le cas où les couples ( A, B) et (C,D ) représentent le même vecteur. On a alors Vous savez que signifie que :
	- (AB) et (CD) sont …………………. .
	- Le sens de « A » vers « B » est le même sens de « ……… » vers « ………… » .( C’est à dire que le quadrilatère n’est pas croisé ).
	- AB = …….
Considérons le quadrilatère « ABCD » . ON vient de dire qu’il est non croisé et qu’il a une paire de côtés ………………….. et de même ……………………….. C’est donc un …………………………... On dira alors : si alors « ABCD » est un parallélogramme.
Inversement : Démontrez oralement que : si « ABCD » est un parallélogramme alors .
Remarque : Dans le cas où « ABCD » sont alignés , nous dirons que le quadrilatère « ABCD » est un parallélogramme aplati.
Théorème : signifie que « ABDC » est un parallélogramme.
Attention : ne vous trompez pas dans la disposition des points : « ABDC » et non pas « ABCD »
Activité : complétez :
signifie « …….. » est un parallélogramme.
Activité n° … :
Dans chacun des 6 cas , placez le point « D » tel que :
v Sachant que « ABCD » est un parallélogramme , vous pouvez écrire les 4 égalités vectorielles :
Et inversement , si l’une de ces égalités est vraie alors « ABDC » est un . …………………………...
Théorème : « A »,  « B » , « C » , « D » étant des points du plan, les égalités suivantes sont équivalentes :
Vecteurs opposés :
Des vecteurs qui ont même direction et même longueur mais de sens contraires sont dits « opposés ».
Exemple : « A » et « B » étant des points quelconques , sont « …………………. ».
Vecteur nul :
A partir d’un couple (A,A’) de points distincts, on a pu définir une translation et le vecteur associé à cette translation. Si les points « A » et « A’ » sont confondus alors ,dans la translation correspondante, chaque point est confondu avec son image. Le vecteur de cette translation a pour longueur « 0 » et sa direction n’est pas définie. Ce vecteur est appelé le vecteur nul. On le note :
			signifie que «  »

Fiche 3 : Milieu d’un segment.		Info @ calcul sur le milieu..
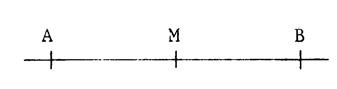
Voici ci-contre un segment et son milieu « M ». Comparons les vecteurs et . « M » est le milieu de signifie :
	- « M » est situé sur (AB ) c'est-à-dire ( AM ) a même direction que ……………. ; AM MB - « M » est entre « A » et « B ». ( Le sens de « A » vers « M » est le même que le sens de « …..» vers « …… » .
Ce qui revient à dire que :
D’où le théorème : « M » est le milieu de signifie que :
Activité 1 :
Ci-contre , on vous donne trois points « A » , « B » , «  C » distincts. Placez le point « E » tel que Placez le point « F » tel que Démontrez que « A » est le milieu de
Activité 2 :
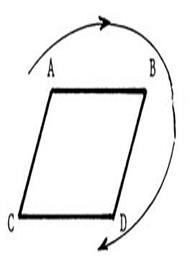
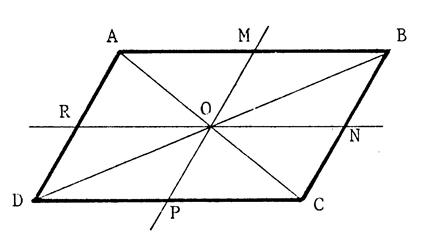
Voici un parallélogramme @ «  » et un point « O ». Placez les points « M » , « N » , «  P » , « R » tels que :  ;  ;  ; Démontrez que «  » est un parallélogramme.

Fiche 4 : Situation problème.
«  » est un parallélogramme de centre « O ». On trace par « O » la parallèle à ( AD ) et ( BC )qui coupe (AB ) en « M » et ( DC ) en « P ». On trace par « O » la parallèle à ( AB ) et ( DC ) qui coupe ( AD ) en « R » et ( BC ) en « N ».
1°) Démontrez ( verbalement , oralement ) que « M », « N » , « P », «  R » sont les milieux des côtés du parallélogramme.
2°) En utilisant les points de la figure , écrivez toutes les égalités vectorielles possibles . (sauf les égalités de vecteur nul). Vous démontrerez oralement ces égalités .
Instructions. Recherchez tous les parallélogramme de la figure. N’oubliez pas les vecteurs tels que : et . Pour vous simplifier la tâche , on a fait deux colonnes : Dans l’une vous écrirez une égalité vectorielle et dans l’autre vous écrirez l’égalité des vecteurs opposés.
Exemple

Fiche 5 Translation et coordonnées.			Translation…@….
On a représenté ci-dessous trois fois la figure « F ».( le polygone «  » )avec le même système d’axes de coordonnées d’origine «  ». Etudes de 3 cas :
Cas 1 :
	Dessinez l’image de la figure « F » dans la translation correspondant au vecteur donné : . Vous appelez : les images de dans la translation de vecteur . Complétez le tableau donnant les coordonnées des images
	A(-2 ;3 )
	B ( -2 ; -1)
	C ( 1 ; -4)
	D ( 3 ;2 )
	O ( 0 ;0 )
Cas 2 :
	Dans chacun des cas , Dessinez l’image de la figure « F » dans la translation correspondant au vecteur donné :  ;
	A(-2 ;3 )
	B ( -2 ; -1)
	C ( 1 ; -4)
	D ( 3 ;2 )
	O ( 0 ;0 )
Cas 3 :
	Dessinez l’image de la figure « F » dans la translation correspondant au vecteur donné :
	A(-2 ;3 )
	B ( -2 ;-1 )
	C ( 1 ; -4)
	D ( 3 ; 2 )
	O ( 0 ;0 )
Comparez , dans les 3 cas, les coordonnées de chaque point avec les coordonnées de son image. Vous constatez alors que : A partir des coordonnées d’un point , pour obtenir les coordonnées de l’image de ce point, - Dans la translation de vecteur , à l’abscisse on ajoute … ., à l’ordonnée on ajoute ….. - Dans la translation de vecteur , à l’abscisse on ajoute  … .., à l’ordonnée on ajoute  …….. - Dans la translation de vecteur , à l’abscisse on ajoute …….., à l’ordonnée on ajoute ……..
Aussi : Le nombre « 3 » que l’on a ajouté à l’abscisse est appelé la « première coordonnée » du vecteur , Le nombre « 7 » que l’on a ajouté à l’ordonnée est appelé la « deuxième coordonnée » du vecteur , ( 3 ; 7 ) est appelé le « couple de coordonnées » du vecteur . On écrira . Complétez de même : ; Ce que vous avez étudié sur trois exemples est vrai dans le cas général.
Théorème : Ayant choisi dans le plan un système d’axes de coordonnées , « M » étant un point quelconque et « M’ » son image dans la translation de vecteur ,