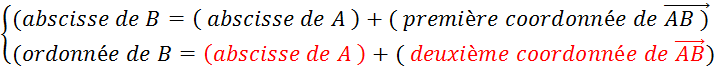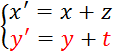Classe de 3^ème collège.
Programme 3^ème .
		Allez vers le corrigé …
	DOSSIER : LES VECTEURS :

Pré requis:

Point : Pré requis : ce qu’est un point..................)
Revoir le cours sur l’addition de deux nombres relatifs@…

ENVIRONNEMENT du dossier:

Index : warmaths

Objectif précédent : - Plan , ligne , point : généralités - Voir : cours de 4^ème - Voir cours précédents pré requis

Objectif suivant : 1°) Le bipoint équipollent 2°) mesure algébrique d'un bipoint sur une droite. 3°) Vers le cours sur « translation et vecteur »

1°) Vecteur : présentation des objectifs.

Fiches 3^ème : Coordonnées - vecteurs dans le plan.

Rappels : Translation et coordonnées. Il est conseillé de travailler les fiches sur « translation-vecteur » ….

Fiche 1 : Coordonnées d’un vecteur.

Fiche 2 : Coordonnées d’un vecteur défini par un couple de points.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Fiche 1 : Coordonnées d’un vecteur.		Info ++@ le repère…..
Vocabulaire : On appelle « repère du plan deux axes de coordonnées de même origine . On dit souvent : « le plan est muni d’une repère d’origine « O » », cela signifie : « on a choisi dans le plan dans le plan deux axes de coordonnées d’origine « O » »
Reprenons la « fiche 5 » de la leçon précédente ( info @@ ) on a Complété :
Cas 1 :	Cas 2 :		Cas 3 :
Dites verbalement ce que vous constatez et essayez de l’expliquer.
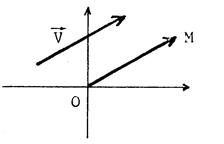
v D’une manière générale , considérons un vecteur quelconque dans le plan muni d’un repère d’origine « O ». Appelons « M » l’image de « O » dans la translation de vecteur on a alors
D’après ce que l’on a vu dans la « fiche 5 @ » , on peut dire : ( abscisse de « M » ) = ( abscisse de O) + ( première coordonnée de ) ( ordonnée de « M ») = ( ordonnée de O) + ( deuxième coordonnée de ) Mais « O » est l’origine , donc ( abscisse de « O » = 0 ) et ( ordonnée de « O »= 0) On dira alors :
Théorème : Dans le plan muni d’un repère d’origine « O » , étant donné un vecteur , en appelant « M » le point tel que , le couple de coordonnées de est égal au couple de coordonnées « M ».
Coordonnées de vecteurs égaux :
Si des vecteurs sont égaux , ils correspondent à la même translation, ils ont donc le même couple de « coordonnées  ». Inversement, si deux vecteurs ont le même couple de coordonnées , ils sont représentés par le même vecteur d’origine « O » , donc ils sont égaux.
Théorème : Si des vecteurs sont égaux alors ils ont le même couple de coordonnées. Si des vecteurs ont le même couple de coordonnées alors ils sont égaux .
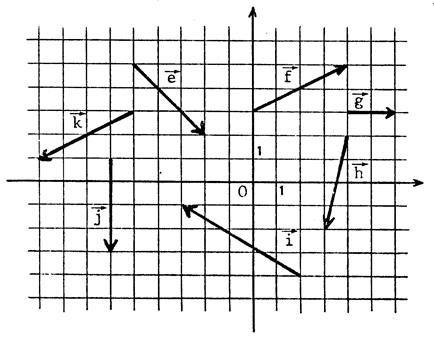
Activités 1 : Donnez les coordonnées des vecteurs représentés ci-contre :  ;  ; ; ; ; ; ; Que pouvez-vous dire des vecteurs :   et  ? ……………………ils sont opposés….. Que pouvez-vous dire de leurs coordonnées ? ………………………elles sont opposées............
Activité 2 :
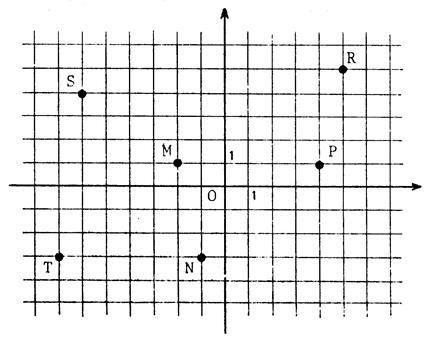
En prenant respectivement comme origine les points : M , N , P , R , S , T dessinez ci-dessous « à droite » un représentant de chacun des vecteurs suivants :  ;  ;  ; ;  ;  ;

Fiche 2 : Coordonnées d’un vecteur défini par un couple de points.
Placez les points : et Lisez les coordonnées de . Vous trouvez :
ON peut considérer que «  » est l’image de «  » dans la translation de vecteur . Grâce au théorème de la fiche 5 ( cliquez ici ) , on peut écrire :
En appelant le couple de coordonnée de .on écrira alors : d’où : on a alors :
Cas général : Dans un plan muni d’un repère, considérons les points et Nous allons calculer le couple de coordonnées de
« B » peut être considéré comme l’image de « A » dans la translation de vecteur grâce au théorème de la fiche 5 ( cliquez ici ), comme précédemment , on peut écrire : d’où