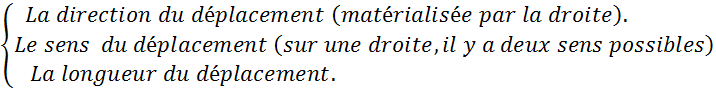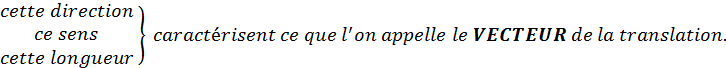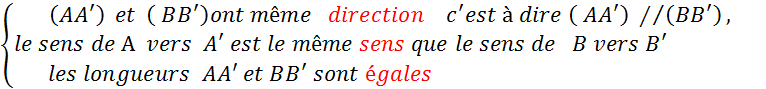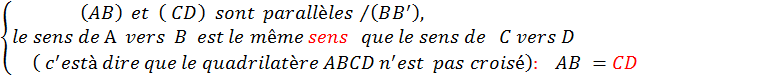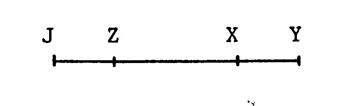la translation de vecteurs collège 4ème .

	Programme 4^ème .		Classe de 4^ème – 3^ème collège.
	Programme 3^ème .
			Allez vers le corrigé …

OBJECTIF : savoir définir un bipoint		DOSSIER : LES VECTEURS :

Pré requis:

Point : Pré requis : ce qu’est un point ..................)

ENVIRONNEMENT du dossier:

Index : warmaths

Objectif précédent :

Plan , ligne , point : généralités

Objectif suivant :

1°) Le bipoint équipollent

2°) mesure algébrique d'un bipoint sur une droite.

3°) Vers le cours sur « translation et vecteur »

1°) Vecteur : présentation des objectifs.

Fiches 3^ème : La translation de vecteurs

	Fiche 1 : Translation.
	Fiche 2 : Vecteur d’une translation.
	Fiche 3 : Image d’un point par un translation.
	Fiche 4 : Vecteurs égaux et parallélogramme.
	Fiche 5 : Exercices.
	Fiche 6 : Image d’une figure par une translation.
	Fiche 7 : Image de figures élémentaires par une translation.

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

	Fiche 1 : Translation.	Info +++@ ++++
	Activités :
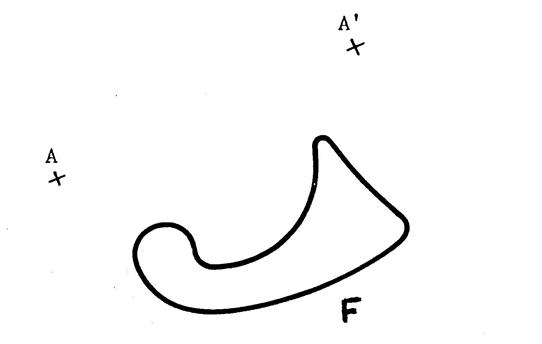
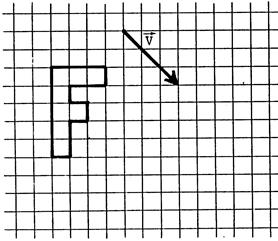
	Ci-dessus : On vous donne u figure « F » et deux points « A » et « A’ ». v Tracez la droite ( A A ‘) . v Prenez du papier calque et calquez ( sans bouger) « F » , « A » et la droite ( A A ‘). v Passez au crayon gris , sur le calque, l’envers du dessin de « F ». v Replacez le calque dans la position initiale et faîtes glisser suivant la droite ( A,A’ ) . (La droite « A A’ » de votre calque doit rester sur la droite (AA’) de la feuille.) Vous arrêtez de faire glisser quand le point « A » du calque arrive en coïncidence avec le point « A’ » de la feuille. Dans cette position , vous décalquez que la feuille le dessin de « F » . On dit que « F’ » est l’image de « F » dans une translation. Remarque : les figures « F » et « F’ » sont superposables.

	v Pour pouvoir effectuer une translation déterminée , il faut connaître :
	Dans la translation effectuée ci-dessus , la donnée du couple de points ( A , A’ ) détermine parfaitement cette translation :
	Quelle est l’image de « A » dans cette translation ? .. A’…..

	Activité : Exercice :
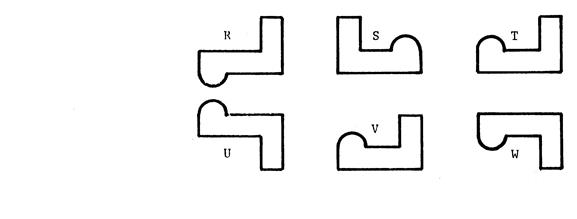
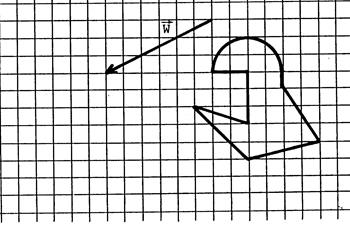
	Parmi les figures ci-dessous , deux d’entre elles se correspondent par une translation. Comme il y a deux façons de les faire correspondre, précisez celle que vous choisissez en complétant : …….à pour image …… Placez ( ci-dessous à gauche ) deux points « O » et « O’ » tels que le couple ( O , O’ )définissez cette translation. Joignez ces deux points par un segment fléché pour indiquer le sens de déplacement.


	Fiche 2 : Vecteur d’une translation.
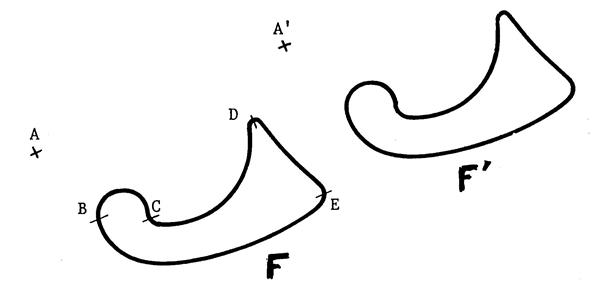
	Reprenez la translation vu dans la fiche 1 .(on vous propose un corrigé) On a marqué sur la figure « F » les points « B » ; « C » ; « D » ; « E » . Placez sur la figure « F’ » les points « B ‘ » ; « C’ » ; « D’ » ; « E’ » images respectives de « B » ; « C » ; « D » ; « E » . Matérialisez par un trait rouge le déplacement de « B » à « B’ » lors du glissement du calque. Faîtes de même pour les points « C » ; « D » ; « E » .

	v Le déplacement du calque s’étant effectué suivant la droite ( A A ‘ ), les traits rouges que vous avez tracés sont donc portés par des droites et toutes ces droites sont parallèles à la droite ( A A ‘). Le sens de déplacement est la même pour tous les points , c’est celui de F vers F’ La longueur du déplacement est la même ^pour tous les points . Donc les segments [ BB’ ] ; [ CC ‘ ] ; [ DD’ ] ; [ EE’ ] ; ont même longueur ; celle de [ AA’ ] .
	v « M » étant un point quelconque de « F » , « M » possède une image et une seule , appelons – la « M’ ». On passe de « M » à « M’ » de la même façon que l’on passe de « A » à « A’ ». C'est-à-dire :


	v La translation étant définie par ( AA’), le vecteur est désigné par se lit « vecteur AA’ ». La flèche signifie qu’il faut lire « vecteur »et indique le sens : celui de « A » vers « A’ ». et ne désignent pas le même vecteur puisque le sens n’est pas le même .
	v La translation peut-être définie par ( B ,B’ ) ; ( C , C’) ; ( D , D’) ; ( E ,E’) etc …. ( M ,M’) donc ; ; ; ; .. etc .. désignent le même vecteur . On peut donc écrire : = = = =
	A retenir : = signifie

	Dessin représentant un vecteur :
	Pour représenter graphiquement un vecteur , on dessine un segment fléché.
	Par exemple : La droite (ST) donne la direction du vecteur . La flèche indique le sens du vecteur. « T » est l’origine et « S » l’extrémité du couple ( T , S ) La longueur de [ TS] donne la longueur (on dira « norme ») du vecteur.

	v Il y a une infinité de couple de points correspondant au même vecteur. v Il y a donc une infinité de façons de représenter graphiquement un vecteur.
	Notation : On a désigné par le vecteur correspondant au couple de points ( dit : bipoint) ( A , A’) , mais on peut désigner un vecteur par une seule lettre . On écrit par exemple : , , , etc….


	Fiche 3 : Image d’un point par un translation.
	Une translation est parfaitement déterminée par la connaissance de son vecteur. O dira alors :
	A retenir : Dans la translation de vecteur , « M’ » est l’image de « M » signifie =
	Activité 1 :	Activité 2:
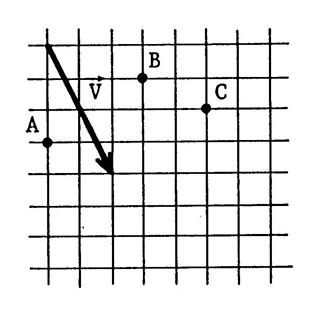
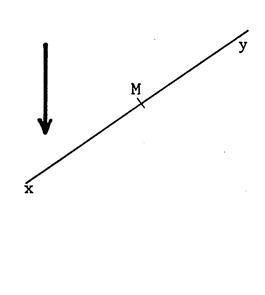
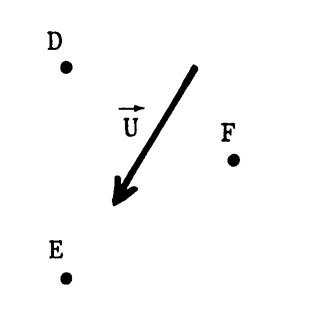
	Ci-dessous . Dessinez les images « A’ » ; « B’ » , « C’ » des points « A », « B » , « C ». par la translation de vecteur	Ci-dessous . Dessinez les images « D’ » ; « E’ » , « F’ » des points « D», « E » , « F ». par la translation de vecteur

	Remarque : Dans toute translation, tout point possède une image et une seule. ( expliquez pourquoi verbalement )


	Fiche 4 : Vecteurs égaux et parallélogramme.	@ Bipoints équipollents
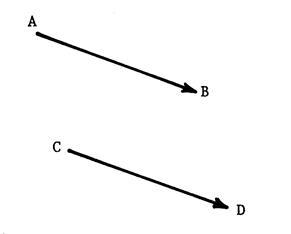
	« A » , « B » ; « C » ; « D » sont 4 points distincts non alignés. Considérons le cas où les couples ( A , B ) et ( C , D ) représentent le même vecteur. On a alors = Vous savez que = Cela signifie :


	v Considérons le quadrilatère « ABCD ». On vient de dire qu’il est non croisé. Et qu’il a une paire de côtés …parallèles …..et de même longueur.. Donc , grâce à la propriété « 15 » ( leçon n°…démonstration parallélogramme…) ; « ABCD » est un parallélogramme. On dira alors que = alors « ABDC » est un parallélogramme.
	v Inversement : démontrez oralement que : si « ABDC » est un parallélogramme alors =

	Remarque : Dans le cas « A » , « B » ; « C » ; « D » sont alignés , nous dirons que le quadrilatère « ABCD » est un quadrilatère aplati.

	Théorème : = signifie que « ABDC » est un parallélogramme.
	Attention : ne vous trompez pas dans la disposition des points : « ABDC » et non « ABCD ».
	Activité 1: = signifie que « HRPS » est un parallélogramme.
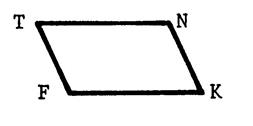
	Activité 2: TNKF est un parallélogramme. Ecrivez 4 égalités de vecteurs.

	Activité 3: JZYX est un parallélogramme aplati. Ecrivez 4 égalités de vecteurs.


	Fiche 5 : Exercices.
	Exercice 1 :
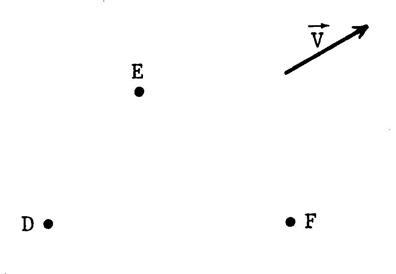
	On donne 3 points « D » , « E », « F » et un vecteur . Placez les images « D’ » , « E’ », « F’ » de « D » , « E », « F » dans la translation . 1°) Nommez les vecteurs égaux à . 2°) Nommez 3 parallélogrammes ( expliquez verbalement ) 3°) Ecrivez 6 égalités de vecteurs. ( ces vecteurs n’ayant pas la direction de .)
	Exercice 2 :
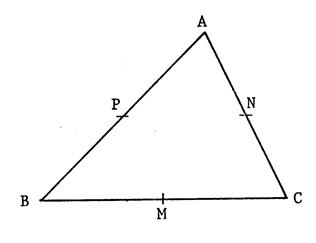
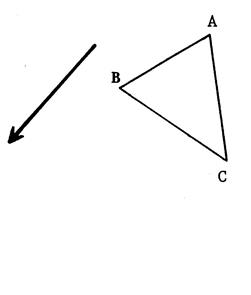
	Ci-contre : voici un triangle « ABC » . « M », « N » , « P » sont les milieux respectifs de [ BC ] , [ CA ] , [AB ] , En utilisant les noms des points « A ; B ; C ; M ; N ; P ». 1°) Nommez tous les parallélogrammes de la figure. 2°) Ecrivez toutes les égalités de vecteurs.
	Exercice 3 :
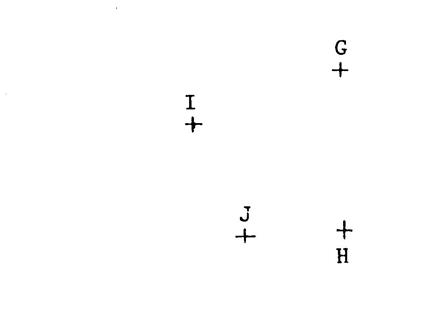
	Voici , ci-contre, quatre points distincts « G ; H ; I ; J ». Dans la symétrie de centre « I » , « G » a pour image « K » ; « H » a pour image « L ». Dans la symétrie de centre « J » , « G » a pour image « R » , « H » a pour image « S ». 1°) Complétez la figure.


Fiche 6 : Image d’une figure par une translation.
En utilisant le quadrillage ( mais pas le calque)
Dessinez l’image de la lettre « F » dans la translation .		Dessinez l’image de la figure ci-dessous dans la translation


Fiche 7 : Image de figures élémentaires par une translation.				Info +++ sur ces translations…
Vous venez de déterminer intuitivement l’image d’une figure par translation dans le plan quadrillé. Vous avez pu constater comme on l’avait dit dans la fiche 1 que toute figure et son image sont superposables. Vous allez le confirmer dans les 3 différents cas ci-dessous. En déterminant l’image de la figure donnée dans la translation de vecteur donné. Pour cela vous pouvez construire l’image de quelques points de la figure.

Droite et demi-droite	Triangle		Cercle

Ce que vous venez de constater, il est possible de le démontrer , nous dirons alors :
Théorème 33 : Dans toute translation , - L’image d’une droite est une droite . La droite et son image sont parallèles. - L’image d’une demi- droite est une demi- droite . de même sens. - L’image d’un segment est un segment de même norme (longueur).. - L’image d’un angle est un angle de même mesure. - L’image d’un cercle est un cercle de même rayon. - Toute surface et son image ont la même aire.

Fiche 8 : Situation problème. ( d’après le sujet donné au brevet en 1987 Caen)

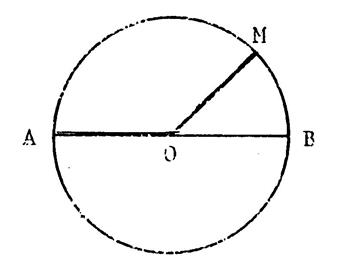
On donne un cercle de centre « O ». [ AB ] est un diamètre et « M » un point du cercle. 1°) Quel est la nature du triangle « AMB » ? (justifiez la réponse) 2°) On considère la translation du vecteur OM. Construisez les points « A’ » ; « B’ » ; « M’ » image de « A ; B ; C » Quelle est l’image de « O » par cette translation ? 3°) Quelle est la nature du quadrilatère « ABB’A’ » ? (justifiez votre réponse )
4°) Démontrez que « AM’B’ » est un triangle rectangle.

Fini le 9/1/2015.