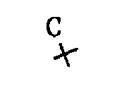Notions  préliminaires

Géométrie

Les outils utilisés en géométrie

Découverte : 

Le POINT :

·      Un corps  très petit, par exemple l’une des fines poussières que l’on voit voltiger dans un rayon de soleil, nous donne l’idée e » point.

·      La trace laissée par la point effilée d’un crayon sur une feuille de papier est un point , mais un point matériel visible en raison de ses dimensions.

·      Le point géométrique , tel que  nous devons le concevoir, n’a aucune dimension ou plutôt a des dimensions nulles ; il n’y a donc rien à dire de la forme d’un point géométrique ; la seule chose à considérer est sa position dans l’espace.

Ordinairement  en géométrie on dessine les figures dont on parle , et , pour plus  de commodité dans le langage, on donne des noms  à ces figures soit au moyen de lettres , soit, au moyen de chiffres .

Ainsi , si l’on trace un point , on mettra à côté la lettre « A » et l’on dira :  soit le point « A » ; On tracera  de même les points  « B » , « C » et « D »  ( figure ci contre)

Les noms  donnés à ces différents points  permettent  de les distinguer facilement les uns des autres.

Représentation graphique d’un point.

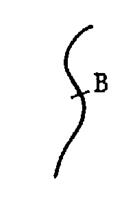
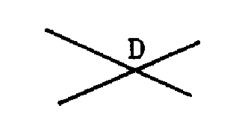
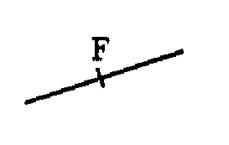
Un point est l’intersection de deux segments de droite ou courbe : 

Remarquez  l’imprécision  qu ‘en à placer la pointe du compas au centre de ces intersections

Ci-dessous d’autres représentations de points.

Dans l’espace : un point est considéré comme étant une droite vue en bout.(prendre une règle à section carré et regarder cette droite en bout .) ; cette droite provient de l ‘intersection de deux plans ou demi-plan.

NOTATION :

Un point est noté par une lettre  majuscule :Pour désigner  plusieurs ou différents points on utilise des lettres majuscules.

On peut aussi désigner plusieurs points par une même lettre , à la condition que celle ci soit affectée d’un signe particulier dans les différents cas on dira :

O’   lire   O prime

O’’ lire    O seconde

O’’’  lire  O tierce

Exemples :

  A ; B   ;   O  (généralement utilisé pour indiquer le centre d’une figure)

 ou  «  x_A »   si le point « A » appartient  à la droite  nommée « x »

 ou    « y_A »  si le point  « A » appartient à la droite nommée « y » ; ainsi de suite

TRAVAUX AUTO FORMATIFS.

CONTROLE

1.      Qu’est ce qu ‘un point ?

2.      Donner trois représentations graphiques d ’ un point.

3.      Que peut représenter un point en géométrie dans l’espace ?

4.      Par quoi nomme - t- on un point ?

EVALUATION :

1.      Faire la représentation des trois types de points

2.      Faire la représentation graphique des trois types de droites :symbolisées par :  ; ( yx) ; (AB)