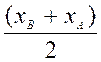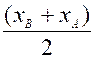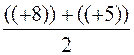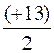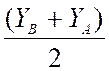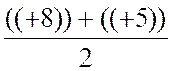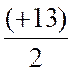|
|
|
|
Longueur d'un segment (la
longueur tient compte de longueur du segment unitaire) |
|
|
Mesure
d'un segment Lla mesure
ne tient pas compte de la longueur du segment unitaire; c'est le cas
le plus utilisé , on dit que le segment unitaire
vaut "1" sans préciser l'unité de longueur) |
|
ENVIRONNEMENT
du dossier:
|
Index
|
|
Projection. |
DOSSIER : Position du MILIEU d'un
segment ( sur une droite)
|
|
|
|
|||||
|
|
-
Représentation graphique. |
|
|||||
|
|
-
Calculs de la position du milieu sur une droite. |
|
|||||
|
|
-
Approche : Calculs de la position du milieu
d’un segment dans un repère cartésien. |
|
|||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Devoir évaluation |
Interdisciplinarité |
|
Corrigé Contrôle |
Corrigé évaluation |
|
+2 +5
|
|
Commentaire:
on cherche une valeur numérique |
|
||
|
|
|
|||
|
|
Schéma(
voir ci-dessus ) : Soit une droite graduée , un point « O » d ‘ abscisse
« 0 » , un point
« I » d ‘abscisse
« 1 » , un point « A » d ‘abscisse « xA »
et un point « B » d ‘« abscisse « xB » *
La position (x M) du milieu ( noté
M) d'un segment est égale à la somme
de l'abscisse de l'extrémité (x B )plus l'abscisse de l'origine (
x A)du segment divisée par deux . |
|
||
|
|
|
xM = |
|
|
|
|
Application: Sur une droite graduée "x"; on trace un segment AB tel que
A= + 5 ; et B
= (+8) ; quelle est la position du point M sur la droite graduée ? |
|
||
|
|
On sait que" le milieu d'un segment est égal à la somme des
valeurs des extrémités" : On peut écrire que : xM = On remplace les
lettres par les valeurs: xM = xM = xM =(+6,5) Conclusion : la position du point M sur la droite graduée
"x" est de (+6,5) Vérification: prendre une graduation égale à un cm. il suffit de tracer une droite , de placer les extrémités du segment , de placer le
milieu sur ce segment, et ensuite de mesurer la longueur qui sépare le point
"M" de l'origine "O" de l'axe . |
|
||
|
|
Ce qui
est vrai pour un axe "x"(droite placée horizontalement) est vrai
pour un axe "y" ( droite placée
verticalement) Schéma: Soit une droite graduée , un
point « O » d ‘ abscisse « 0 » , un point « j » de mesure « 1 » , un point
« A » nommé « yA » et un point « B » nommé « yB »
* Nous aurions la formule
suivante :
|
|
||
|
|
YA et YB sont les positions des points A et B sur
la droite "y" yM = |
|
||
|
|
Application: Sur une droite graduée "y" ; on trace
un segment AB tel que A= + 5 ; et B = (+8) ; quelle est la
position du point M sur la droite graduée ? |
|
||
|
|
On sait que" le milieu d'un segment est égal
à la somme des valeurs des extrémités" : On peut écrire que : yM = On remplace les lettres par les valeurs: yM = yM = yM =(+6,5) Conclusion : la position du point M sur la droite
graduée "y" est de (+6,5) Vérification: prendre une graduation égale à un cm. il suffit de
tracer une droite , de placer les extrémités du segment
, de placer le milieu sur ce segment, et ensuite de mesurer la longueur qui
sépare le point "M" de l'origine "O" de l'axe . |
|
||
|
|
Généralisation : Si nous désignons par « REMARQUE: Si ces deux droites se coupent alors nous sommes
en présence d'un repère cartésien |
|
||
|
Pour en savoir plus : sur les coordonnées du milieu d'un segment. |
|
|
Travaux auto formatifs. |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
A quoi est égal la position du milieu d'un
segment sur une droite graduée? Donner la formule permettant de calculer la
position du milieu d'un segment sur une droite graduée? |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
EVALUATION
Calculer le milieu des segments AB Exercice n°
1 : |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
+2 +5 a = + 2 ;
b = + 5 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
Exercice n° 2 :
B O A a = + 4 ;
b = -1 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
