|
Géométrie : DOSSIER : Plan sous ensemble de
plan . |
|
|
|
|
|
|
|
ENVIRONNEMENT
du dossier:
|
Objectif
précédent : |
|
||
|
|
|
|
|
DOSSIER : LE SEGMENT de droite
|
|
|
|||||
|
|
1. Définition. |
|||||
|
|
2. Longueur d’un segment
de droite. |
|||||
|
|
3. Segments consécutifs’
segments cumulés. |
|||||
|
|
4.
Tracer d’un segment : |
|||||
|
|
5. Comparaison des segments |
|||||
|
|
6.
Les « bornes » du
segment. ( « ouvert » ;
« fermé » ; « semi ouvert » ; « semi
fermé » ; tracés et notations) |
|||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|
|
|
|
|
|
TEST |
COURS
|
|
||||
|
|
Objectif suivant :segment (intervalle)
et règle graduée |
|
|
1- Définition |
|
|
|
|
Un segment de droite est une portion de droite limitée dans les deux
sens par deux points appelés les « extrémités » du segment . |
|
|
|
|
|
|
|
|
|
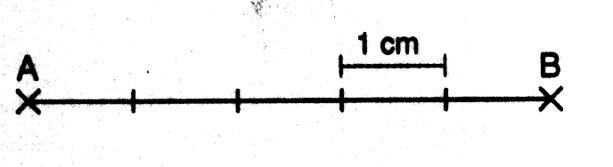
2- Longueur d’un segment de droite . |
|
|
|
|
Une droite illimitée indique simplement une direction et n’a pas une longueurs déterminée, de même une semi droite indique une direction à partir d’un point origine, mais n’a pas
non plus de longueur déterminée. Au contraire un segment de droite a une longueur fixe, comprise entre
ses deux extrémités ; dés lors deux segments
de droite peuvent être comparés au point de vue de leurs longueurs, tandis
que pareille comparaison est
impossible entre deux droites ou deux semi droites. |
|
|
|
|
|
|
|
|
|
3 ° ) Segments
consécutifs’ segments cumulés. |
|
|
|
|
Considérons , sur
une même droite « XY » , trois ponts « A »,
« B » et « C » , disposés , par exemple, suivant l’ordre
alphabétique ( vois figure ) |
|
|
|
|
Ces points déterminent trois segments « AB » , « BC » et « AC » que l’on peut
grouper deux à deux des trois façons suivantes : « AB » et « BC » ; « AB » et
« AC » ;
« BC » et « AC » |
|
|
|
|
Les deux segments « AB » et « BC » qui ont une
extrémité commune « B » et sont situés de part et d’autre de cette extrémité ,
sont dits « consécutifs » ; Les deux segments
« AB » et « AC », qui ont une extrémité commune
« A » et sont situés d’un même côté de cette extrémité, sont dits
« cumulés », il en est de même des segments « BC » et
« AC ». |
|
|
|
|
|
|
|
|
|
Si l’on a , sur une même droite
« XY », plus de trois points, « A », « B »
,« C », « D », « E » disposés , par exemple, |
|
|
|
|
Suivant l’ordre alphabétique , on dit encore que les segments
« AB » , « BC » « CD » et « DE »,
pris dans cet ordre ou dans l’ordre inverse « ED » ,
« DC », « CB » et « BA », sont consécutifs ,
et que les segments « AB » , « AC » , « AD » et
« AE » pris dans un ordre
quelconque ,sont cumulés. |
|
|
|
|
|
|
|
|
Exemples ; |
|
|
|
|
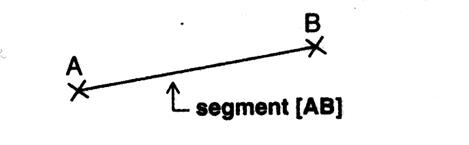
La partie de droite comprise entre deux points est
appelée « SEGMENT »
|
Tracer un morceau de droite c’est tracer un segment de droite : |
|
|
||
|
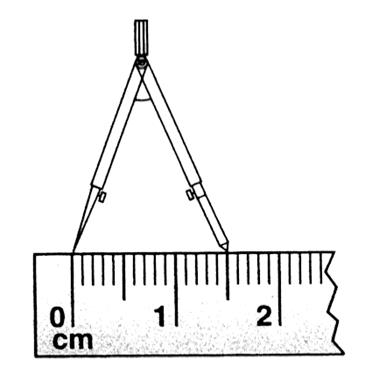
Le premier segment étant tracé . Il suffit de tracer une ligne . Sur cette ligne on
place un point. Avec un compas on
prend la mesure du premier segment . En prenant soin de conserver le même écartement
on reporte le deuxième point sur la ligne . (il suffit de gommer ensuite les parties de
la ligne n’appartenant pas au nouveau
segment.) |
|
|
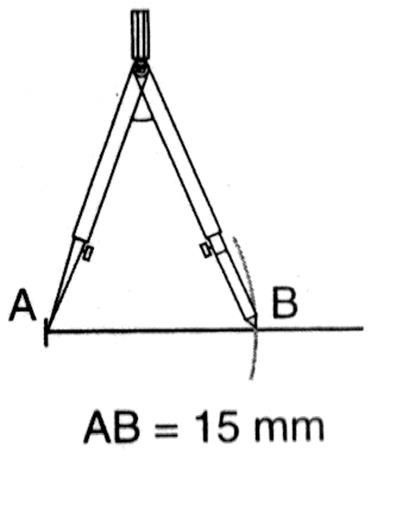
COMPARAISON des segments :
|
Manip : tracer sur une feuille un segment de droite AB , traçons sur un papier calque un segment de droite
CD ; Amenons le calque sur le dessin de manière à amener les deux
droites l’une sur l’autre, le point A coïncidant avec le point C |
|
|
|
|
Suite :
|
Les pointillés sont
hors « segment » , le trait plein
appartient au segment considéré. |
Le
crochet est « ouvert » ou
« fermé », -« ouvert » la borne n’appartient pas au segment. -« fermé »
la borne appartient au segment. |
|
|
|
|
Nom |
Représentation
graphique : Activités : Traduction de l’écriture symbolique. ·
sur une droite placé les points « A » et « B » ·
dessiner les crochets « ouvert » et ou « fermé » |
Notation |
|
il
contient les points qui le borne |
|
[A B] |
|
|
|
|
|
Segment ouvert : Il ne
contient pas les points qui le borne |
|
]
A B [ |
|
|
|
|
|
Autres cas : Segment semi ouvert : il contient un des points qui le borne. Soit celui de droite : (il exclu celui de gauche
) soit celui de gauche : (il exclu celui de droite
) |
|
] A
B ] [A
B[ |
|
|
|
]
A B ] |
|
|
[ A B [ |
|
|
Nom |
représentation graphique |
Notation |
||||||||
|
Segment fermé : il
contient les points qui le borne |
|
[A B] |
||||||||
|
B A Il ne
contient pas les points qui le borne |
|
] A B [ |
||||||||
|
B A B A
il contient un des points qui le borne. Soit celui de droite : (il exclu celui de gauche
) soit celui de gauche : (il exclu celui de droite
) |
|
]A
B] [A B[ |
Application : en algèbre ; pour représenter graphiquement des valeurs de
« x » ; solutions des inéquations du premier degré à une
inconnue et en relation avec les relations d’ordre.
exemples :
Représenter
graphiquement +4 £ x £ +15 ; ( lire : « x » est compris entre les valeurs +4 inclus et +15
inclus )
[A B] ...on notera ...... [ +4 ;
+15 ]..........................................................
![]()
![]()
![]() on dessinera : [ ]
on dessinera : [ ]
0 +4 +15
] A B [ ..........................................................................................
] A B]
............................................................................................
[A B [
...........................................................................................
] A x )
..........................................................................................
[ A x )
...........................................................................................
CONTROLE :
Traduire et faire une représentation graphique.
[A B]
........................................................................................
] A B [ ..........................................................................................
]A B]
............................................................................................
[A B[ ...........................................................................................
EVALUATION
Faire la représentation graphique
des segments de droites
suivants :
[+5 ; +7]
] –6 ; -3 [
]-1 ; + 2,5]
[0 ;+ 3[
Voir en histoire : les dates
historiques d’événements qui ont eu lieu
voilà ……
1°) Sciences naturelles : la
vitesse des animaux
|
Informations : voici les vitesses de certains animaux |
|
|
En prenant
Géographie : Les longueurs des grands fleuves français .
|
Ces 4 segments de droites
figurent les 4 grands fleuves français. Légende : chaque cm représente |
|
|
Questions :
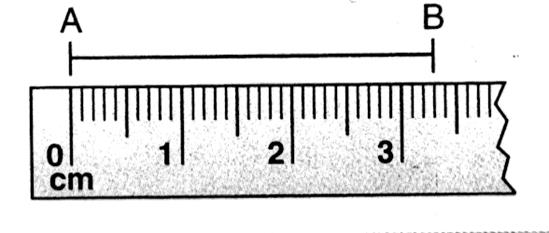
Mesurer la longueur de chaque segment.
Calculer la longueur de chaque fleuve .
|
|
Loire |
Rhône |
Seine |
Garonne |
|
Lg en cm |
|
|
|
|
|
Lg en km |
|
|
|
|