|
|
|
Pré requis:
|
|
|
ENVIRONNEMENT du
dossier:
|
1.
Primaire : les lignes 2.
Le point |
v
Droite v
½ droite v
Segment v
½ plan |
|
DOSSIER :
Nomenclature N°2 : DROITE (suite)
1/2 DROITE ; et « Plan et demi Plan »
, SEGMENT et milieu d’un segment.
|
|
|
|
|
|
|
|
|
|
TEST |
COURS |
Devoir évaluation |
Interdisciplinarité |
|
|||
|
|
|
|
|
|
|
||
Une droite est l’intersection de deux - demi plans .(
activité :plier une feuille , l’arête
·
Axiome d ’ Euclide : Par deux points « A » et « B » passe une
droite est une seule .
2°) La ligne « droite »
La
droite est illimitée : La représentation graphique ; toute représentation par le dessin d ‘ une ligne droite n ‘est en fait qu
‘une partie de la droite ( appelé « segment »).
L’outil couramment
utilisé pour tracer une
« droite » est une « règle ».
(voir
les différentes règles ..........................................@......)
3°) NOTATION : il y
a 3 façons de traduire ; avec
des symboles ; une droite
soit : droite :
« » ou
« d » ou droite
yx
noté ( y x ) ou
; « droite AB » noté
(AB)
C A
Remarques
·
le point C n’appartient pas à
la droite AB :
ce qui se note : C Ï (AB)
·
Le point D appartient à la droite
AB
ce
qui se note : D Î (AB)
Par définition : Une droite
est une ligne telle qu ‘elle réalise
toujours le plus court chemin entre deux quelconques de ses points
,
« Illimitée » : par deux points passe une droite et une seule.
PLAN et Le
1/2 PLAN
·
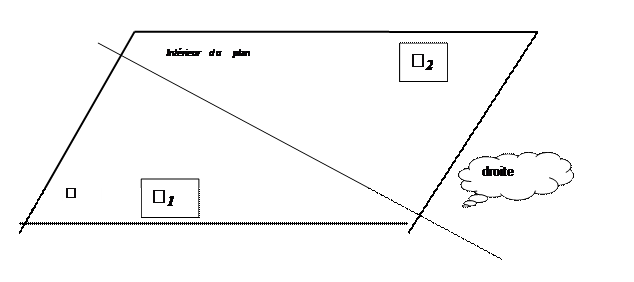
Un plan est une surface plane de dimensions illimitées de tout part . Le dessin que l’on en fait n’en représente qu‘une infime partie.
Toute droite contenue dans un plan partage celui ci en deux parties égales appelées "demi
plans". La ligne droite sert de frontière entre ces deux demi plans .
NOTATION : La lettre utilisée pour désigner un
demi plan est un « p » majuscule indicié : 1 et 2
Exemple de représentation :
|
Objectif suivant : la demi droite et axe gradué |
Tout point d ’ une droite
partage celle - ci en deux demi droites :
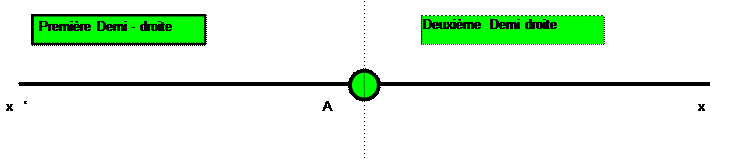
LA DEMI DROITE FERMEE
Une demi
droite est dite « fermée » si elle contient le point qui la limite
|
Notation : [ A x ) ; lire
demi droite fermée « A
x » ; Le point « A » appartenant à la demi droite. |
|
a
[ notation : x ³ a |
A DEMI DROITE OUVERTE
x
Une demi droite est dite « ouverte » si
le point qui la limite n’appartient
pas à la demi droite considérée , le point est dit « origine » de la
demi droite.
|
Notation : ] A x ) ; lire : demi droite ouverte « A x » ;
« A » n’appartenant pas à la demi droite |
|
Objectif suivant :segment
(intervalle) et règle graduée |
« SEGMENT »
La partie de droite comprise entre deux points est
appelée « SEGMENT »
« SEGMENTS ISOMETRIQUES » deux segment
sont isométrique si ils ont la même mesure .(longueur)
« BORNES »ou
« extrémités »
Les deux points limitant le segment s’appellent :
« bornes ou extrémités»
|
Nom |
représentation graphique |
Notation |
||||||||
|
il
contient les points qui le borne |
|
[A B] |
||||||||
|
B A Il ne
contient pas les points qui le borne |
|
] A B [ |
||||||||
|
B A B A
il contient un des points qui le borne. Soit celui de droite : (il exclu celui de gauche
) soit celui de gauche : (il exclu celui de droite
) |
|
]A
B] [A B[ |
Application : en algèbre ; pour représenter graphiquement des valeurs de
« x » ; solutions des inéquations du premier degré à une
inconnue et en relation avec les relations d’ordre.
exemples : ³<
Représenter
graphiquement +4 £ x £ +15 ; ( lire : « x » est compris entre les valeurs +4 inclus et +15
inclus )
[A B] ...on notera ...... [+4 ;
+15]...............................................................................
on dessinera :
[
]
0 +4 +15
] A B [
..........................................................................................
]A
B]
............................................................................................
[A B[ ...........................................................................................
] A x )
..........................................................................................
[ A x ) ...........................................................................................
Donner l ‘axiome d ‘
Euclide :
Traduire et faire une représentation
graphique.
......................................................................
( yx )
............................................................................
(AB)...........................................................
C Ï (AB)
..........................................................................
D Î (AB)
.................................................................................
[A B]
........................................................................................
] A B [ ..........................................................................................
]A B]
............................................................................................
[A B[
...........................................................................................
] A x )
..........................................................................................
[ A x
)
...........................................................................................
Qu ‘est ce qu
‘une droite ?
.................................................................................
CORRIGE :
Droite : ou droite yx noté ( yx
) ou ; droite AB noté
(AB)