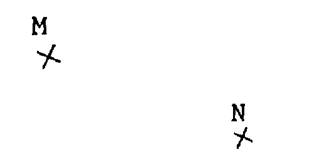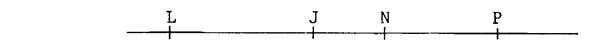la droite _ le segment ; le milireu , les droites parallèles .

Revu 2012-06-30

Pré requis:

Notions préliminaires
Ligne droite (notion)		CM2 _ 6^ème.

ENVIRONNEMENT du dossier:

Index « warmaths »

Objectif précédent :

1°) droite et courbe : vue en primaire.

2°) Droite passant par un ou plusieurs points

3°) La ligne droite

Objectif suivant :

Info 1 : Liste des cours en géométrie.

Info 2 : Tableau

Info 3 : la géométrie en arithmétique

DOSSIER : DROITE – DEMI DROITE - SEGMENT – MILIEU - DROITES PARALLELES

Chapitres
	1. Le point
	2. La droite et « points alignés »
	3. La demi droite
	4. Le segment
	5. Le milieu d’un segment.

			ICI : Travaux auto- formatifs.			Corrigé des travaux auto formatifs.
TEST		COURS	Devoir Contrôle	Devoir évaluation	Interdisciplinarité : Travaux dos.46	Corrigé Contrôle	Corrigé évaluation

Info COURS

1	Le point ( info +++)
	Ci-dessous la représentation de points.


	On remarque que le dessin du point occupe une « certaine » place.
	Mais , le point mathématique n’occupe pas de place.


2	La droite.
	Activité 1
	a) Tracé :

	On vous propose deux points « M » et « N ». Avec une règle tracer un trait passant par « M » et « N ». Le trait représente une portion de la droite. Cette portion de droite « matérialise » une droite . Il reste à imaginer cette droite , on pense qu’elle se prolonge des deux côtés ; indéfiniment. ( elle quitte la feuille ).
	On dit que par les deux points passent une seule droite. (d’autres parleront : propriétés et axiome d’Euclide »
	· Et la droite passant par « M » et « N » ou « N » et « M » . est appelée droite MN ; ou droite NM . · Pour désigner la droite MN , en géométrie on écrira en écriture symbolique : ( M N ) : ( deux lettres majuscules entre parenthèses) Ou bien : · Pour désigner la droite NM , en géométrie on écrira en écriture symbolique : ( NM ) : ( deux lettres majuscules entre parenthèses)
	b) Compléments sur la désignation d’une droite :
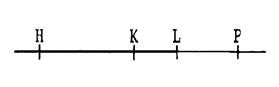
	Activité : Ci contre une droite et quatre de ses points. On appelle cette droite : ( H K) ; ( K H) ; (HL) ; ( LH) ; ( H P ) ; ( PH ) ; (KL) ; (L K) ; ( K P ) ; ( P K ) ; ( L P ) ; ( P L)
	· On peut désigner une droite par une lettre : « D » ; « d » ; « m » ; « s » ; d’ » ; « x ‘ » ; « x ‘ ‘ » … ; « x » ; « y » …..Mais on utilise des lettres grecques :exemple « » qui est la lettre « delta ».
	On peut utiliser aussi deux lettres « x » et « y » , par exemple et on dit « droite xy » Attention : dans ce cas « x » et « y » ne sont pas des points.

	Quand on veut représenter un point sur une droite on trace un petit trait et on écrit son nom à côté (on nome ce point) Ainsi dans l’exemple ci-dessous ,on a placé le point « O ». Activités : Placer d’autres points sur la droite et donner leur un nom . Question : · Combien peut –on placer de point sur cette droite ? ( une infinité)
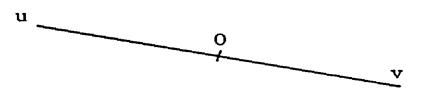
	· Combien y a-t-il de point sur la droite uv ? ( un seul )
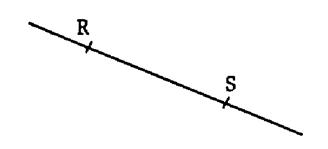
	· Combien y a t –il de point sur la droite RS ? ( deux points)
	Remarque : Sur la droite RS , il y a deux points qui portent un nom : « R » et « S » , mais il y en a une infinité d’autres auxquels on n’a pas donné de nom.

POINTS ALIGNES :

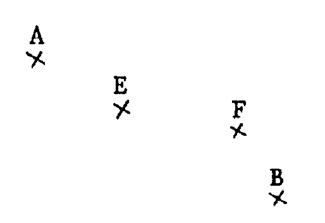
Ci-dessous on vous donne 4 points : A ; E ; F ; B .

Activités :

· Tracer une droite passant par A et B , on nome la droite (passant par A et B) « d »

· Que constatons pour le point « E » : réponse : le point E se trouve sur la droite « d ».

· Que constate –t-on pour le point « F » réponse : le point F ne se trouve pas sur la droite « d ».

On retiendra : quand une droite passe par plusieurs points , on dit que ces points sont alignés…..

On dira que les points A ; B ; E sont alignés et que les points ABF ne sont pas alignés.

· Dans le cas de deux points seulement , est-il besoin de dire qu’ils sont alignés ? réponse : NON


3	Demi droite . (info1 : la demi droite) ; ( @ info 2 : demi – droites et angle )
	· Les points de la droite « xy » situés du même côté du point « M » constituent un ensemble que l’on appelle une « demi-droite » · Le point « M » détermine sur « xy » , deux demi-droites que l’on note : [ Mx et [ M y . « M » est ( appelé) l’origine de ces demi- droites. La droite « xy »est le support de ces demi-droites. · Activité 1 : passer en bleu la demi-droite [ Mx et en rouge la demi droite [ M y .
	Activité 2 :
	Nommer toutes les demi- droites que vous voyez sur cette figure.
	Réponse : a) [Ov et [ I v ; [ Ou . . [ I u . Remarques : · La droite qui se note [Ov peut se noter [ I v · De même la droite [ Ou peut se noter [ I u .


4	Le segment ( info@ plus)
	L’ensemble des points de la droite « d » situé entre « A » et « B » est appelé « segment » ; On le note [ AB ] ou [ BA ] Activité : Coloriez en bleu le segment : [ AB ] · « A » et « B » sont appelés les « extrémités » du segment. La droite ( A B ) est le support de ce segment. · Il y a une infinité de points sur ce segment.
	ATTENTION : Il ne faudra pas confondre les notations suivantes : · ( A B ) : désigne une droite ; elle est illimité des deux côtés. · [ A B : désigne une demi droite ; Elle est limité en « A » et illimité de l’autre côté. · [ AB ] : désigne un segment , il est limité en « A » et en « B »
	Activité :
	Nommer par écrit tous les segments ayant pour extrémités deux points des quatre points : « L » ; »J » ; « N » ; « P »

	Réponses : [ LJ ] ; [ LN ] ; [ LP] ; [ JN ] ; [ JP ] ; [ NP] ; [ PL ] ; [ PN ] ; [ PJ] ; [ NJ ] ; [ NL ] ; [ JP] ;
	ACTI V I TES : Recherche des points situé ou non sur une droite , une demi- droite ou un segment.
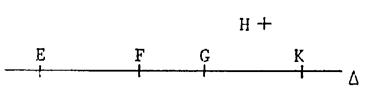
	On donne une droite delta , « » et des points : E ; F ; G ; H ; K. · Pour exprimer que « E » est un point qui appartient à la droite « » ; on écrira : · Pour exprimer que « H » est un point qui n’ appartient pas à la droite « » ; on écrira : · De même que « F » est un point du segment [ E G ] qui peut s’écrire : · « K » n’est pas un point de la demi droite [ GE on peut écrire Activité1 : Compléter les écritures suivantes en utilisant les symboles : et : E ………..[ F K ; F …..[ G E ; G …………[ FK ] ; K …..( G F ) ; K …..[ G F ] ;

	Activité 2 :
	Ci-dessous o vous donne une ligne « zt » . « C » et « D » sont deux de ses points . On vous demande de placer sur cette droite : n( on dit aussi : positionner)
	1°) Un point « A » tel que : M [ CD ] 2°) Un point « B » tel que : B [ C t ; et B [ CD ] 3° ) Un point « F » tel que F [ D t ; et F [ C z 4°) Un point « P » tel que P [ D t ; et P [ C t

	Activité 3 :
	Placer sur la droite « xy » , quatre points : M ; N ; P ; Q de telle sorte que : M [ D y ; N [ CD ] ; et P [ CD ] et Q [ By


5	Le milieu d’un segment.	( ici info 1 plus sur le segment et son milieu). (info 2 : la division d’un segment) Info 3 : voir programme 4 ème « le milieu » dans les triangles) ; info 4 : cours sur les milieux dans les triangles.
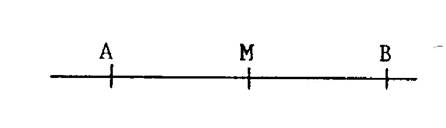
	Voir la figure ci contre. « M » est le milieu du segment. [ AB ] · « M » est un point du segment. [ AB ] · « M » est à égale distance de « A » et de « B » En conclusion : Les segments [ MA ] et [ MB ] ont donc la même mesure.
	Ce qu’il faut vérifier avec une règle graduée ( pour obtenir la longueur) , ou un compas pour comparer les mesures (normalement) égales.
	Activité : Tracer la position du point « R » , milieu du segment « M P » Procédure : · 1°) Mesure la longueur du segment : : Mes. [ MP ] = ………………………mm · 2°) Diviser par « 2 » la valeur de la mesure du segment [ MP ] : ………….longueur MR ou RP = ( Mes. [ MP ] ) / 2 ) = ………………………mm · 3°) Reporter la distance sur le dessin. ( · 4°) Vérifier que le point « R » est a égale distance des points « M » et « P » .
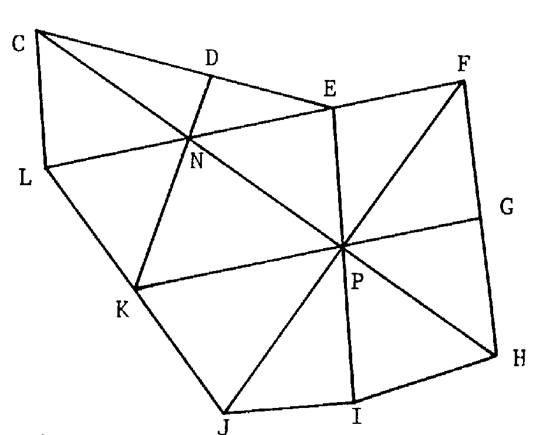
	Activité 2 : Trouver l’ensemble des points qui semble être le milieu d’un ou plusieurs segments.

	Les réponses seront écrites sous la forme : · P est le milieu de [ F H ]







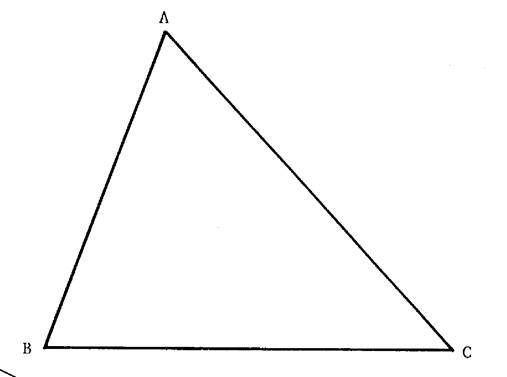
	Activité 3 : On donne un triangle A C B : On demande : ( utiliser la règle graduée ) 1°) Déterminer la mesure de AC , calculer la mesure de la distance qui sépare «M » équidistant de[ AC ]et Placer un point « M » milieu de [ AC ]. Ainsi de suite : 2°) Placer un point « N » milieu de [ CB ] 3°) Placer un point « P » milieu de [ BA ] Ensuite tracer les droites : ( MN ) ; ( N P ) ; ( P M)
	Remarque importante : Quand on demande de tracer la droite ( exemple : ( M N) ) on n’arrête pas le trait aux points « M » et « N » , on doit continuer le trait , on doit « dépasser » les points « M » et « N » . Sinon : on répond à une autre question : « tracer le segment MN ».
	Exemples :
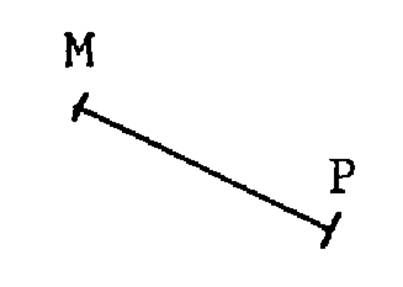
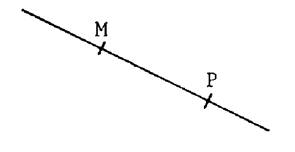
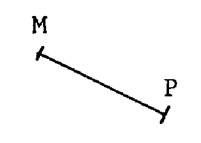
	· ci-dessous , on répond à la question : Tracer le segment « MP »		· ci-dessous , on répond à la question :Tracer la droite « M P »

TRAVAUX AUTO FORMATIFS

CONTROLE :

1) Citer les deux propriétés de la droite.

2 ) Citer les trois sortes de droites.

3) quel est l’outil que l’on utilise pour tracer une droite ? quelle précaution doit – on prendre ?

EVALUATION

Tracer une droite avec une règle.

(comment vérifier ! si elle est rectiligne )

Aller revoir les activités dus cours..

INTERDISCIPLINARITE