ENVIRONNEMENT du dossier:

>>>> Aide >>>>>>

DOSSIER : LES DROITES des MILIEUX

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

Classe de 4^e :Connaître et utiliser les théorème suivants relatifs aux milieux de deux côtés d’un triangle .

Résumé à retenir :

Théorème 1 : Dans un triangle , si une droite passe par les milieux de deux côtés , elle est parallèle au troisième .

Théorème 2 : Dans un triangle , si une droite passe par le milieu d’un côté et est parallèle à un second côté , elle coupe le troisième en son milieu.

Théorème 3 : Dans un triangle , la longueur du segment joignant les milieux de deux côtés est égale à la moitié de celle du troisième côté.

Théorème 1 :

Enoncé : Dans un triangle , si une droite passe par les milieux de deux côtés , elle est parallèle au troisième .

INFO PLUS+++

La droite qui relie les milieux de deux cotés d’un triangle est parallèle au troisième côté.

Commentaire :il y a dans un triangle trois droites des milieux.

Théorème 2

Enoncé : Dans un triangle , si une droite passe par le milieu d’un côté et est parallèle à un second côté , elle coupe le troisième en son milieu.

b’

a’

b

a

Construction de droites milieux des cotés dans un triangle :

Remarque :

lg. a = lg. b et lg. a’ = lg. b’

utilisations : graduations régulières , division d’une droite en segments égaux.

A

Procédure :

Tracer le triangle.

Sur un coté déterminer le milieu « A » (par mesure , ou par construction)

A partir de ce point tracer les parallèles au deux autres cotés

Terminer la construction :tracer la troisième droite soit en joignant les deux milieux soit en traçant la troisième parallèle passant par un point « milieu

Théorème 3

Enoncé : Dans un triangle , la longueur du segment joignant les milieux de deux côtés est égale à la moitié de celle du troisième côté.

Le segment qui relie les milieux de deux côtés d’un triangle a une longueur égale à la moitié de la longueur du troisième coté.

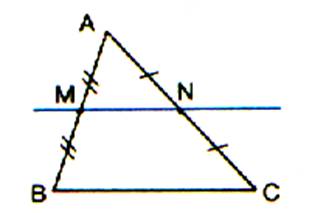
Si M est milieu du segment AB et

N est milieu du segment AC alors on en conclut que la droite MN et parallèle à la droite BC

La distance entre MN est égale à la distance entre BC divisée par 2

Autrement dit :

( MN) //(BC)

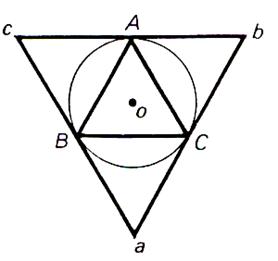
CAS particulier :INFO PLUS le polygone régulier ( tracé) :

Remarque : Un polygone régulier est inscrit dans un cercle.

Si l’on trace par chaque sommet d’un polygone régulier la tangente au cercle , on construit un polygone régulier ayant la même nombre de côtés.

TRAVAUX AUTO- FORMATIFS.

CONTROLE:

1°) Compléter les phrases suivantes :

La droite qui relie les milieux de deux cotés d’un triangle ……………côté.

2°) Le segment qui relie les milieux de deux côtés d’un triangle a une longueur égale ……………… de la longueur du troisième coté.

3°) Citer les 3 théorèmes relatifs « aux milieux »

EVALUATION:

1°) Tracer un triangle quelconque : et tracer les droites des milieux .

2°) Droite des milieux d' un triangle .

a) Construire un triangle de côtés AB = 6 cm , BC = 7 cm et AC = 8 cm . Placer le point M au milieu du segment [ AB ] et tracer la parallèle à [ BC] qui coupe [A C] en N .

b)Appliquer la relation de Thalès pour prouver que N est le milieu de [ AC] . La droite ( MN ) est dite « droite des milieux » .

b) Construire les deux autres droites des milieux du triangle .