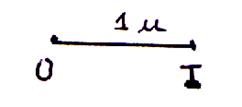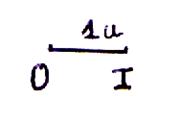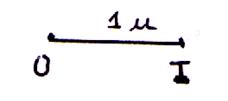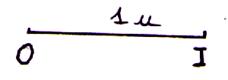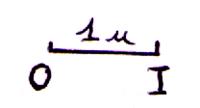Pré requis:
|
|
||
|
Préambule |
||
|
Soustraction de deux nombres relatifs |
||
ENVIRONNEMENT du dossier:
|
Objectif précédent
mesure algébrique notée :
|
DOSSIER : DISTANCE entre deux points sur une droite
.
·
DEFINITIONS
· Notation : d ( O,E ) = ½![]() ½ ;
½ ;
·
CALCUL de la DISTANCE entre deux points sur une droite.
·
Exemples : par la méthode graphique , par le
calcul.
|
TEST |
COURS |
Interdisciplinarité |
|
DEFINITIONS
1°) ON appelle "mesure" l'évaluation d'une quantité en la
comparant à une quantité déterminée.
2°) On appelle "longueur" la dimension d'un objet linéaire de
l'une à l'autre de ses extrémités.
(l'unité de longueur est le mètre)
3°)On appelle "distance" ,l'intervalle (ou les intervalles )qui existe
entre deux points ,ou deux objets. .(on dit aussi que
c'est le nombre de graduations qui sépare de points sur une droite)
(L'intervalle est généralement noté "u" associé à un segment
de droite d'unité "UN ") ,
|
on confond souvent « distance » et
« longueur » ! On peut dire que la distance entre deux points
se mesure avec un instrument gradué appelé « mètre » , avec le mètre nous mesurons la longueur entre deux
points. La longueur est une forme de vue «
restrictive » de la distance. Dans la distance,
le nombre de graduations n’est pas associé à un nom. Exemple : la distance entre A et B est de « 12 graduations » Dans la longueur , le nombre
de graduations est associé à un nom . Exemple : la distance entre A et B est de ,par
exemple « 12 centimètres » |
Pour obtenir la
distance entre les deux points A et B
Il y a
2 solutions possibles ; une solution graphique ou une solution par calcul
:
La
distance entre deux points :elle se
calcule ; c’est la valeur absolue du nombre relatif obtenue
faisant le calcul d'une mesure algébrique .
Ou elle se détermine aussi graphiquement
, il suffit de compter le nombre de graduations qui sépare les deux
points. (la distance est un nombre
décimal qui n ’ a pas
d’unité de longueur.
La distance entre deux points servira à connaître ,
en effectuant un calcul , la longueur
d'un segment .
I ) Obtention de la distance entre
deux points ,à partir d’une représentation graphique ,sur une droite par
« comptage » :
Pour obtenir la distance entre
deux points sur une droite il suffit de
compter le nombre de graduations ( ou intervalle) qui
sépare les deux points considérés .
On la note d ( O, E ) ou d ( A,B )
Remarque : d ( A,B ) = d ( B,A )
Attention ne pas confondre avec la mesure algébrique de (A,B) qui est
différente de la mesure algébrique de
(B,A) ; les valeurs sont « opposée »
Exemple de
problème :
trouver graphiquement la distance entre
A et B :

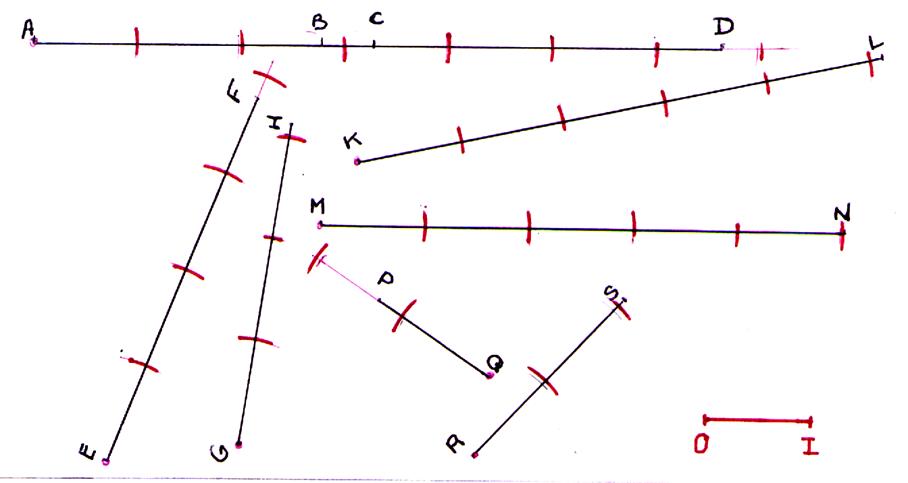
On gradue la droite
, en reportant avec un compas la
distance OI ; on numérote chaque graduation .
On
compte le nombre d’intervalles séparant les points A et B .
Analyse :
il y a deux graduations entre A et B , ( quelque soit le sens du comptage ) .
La distance en A et B est 2
|
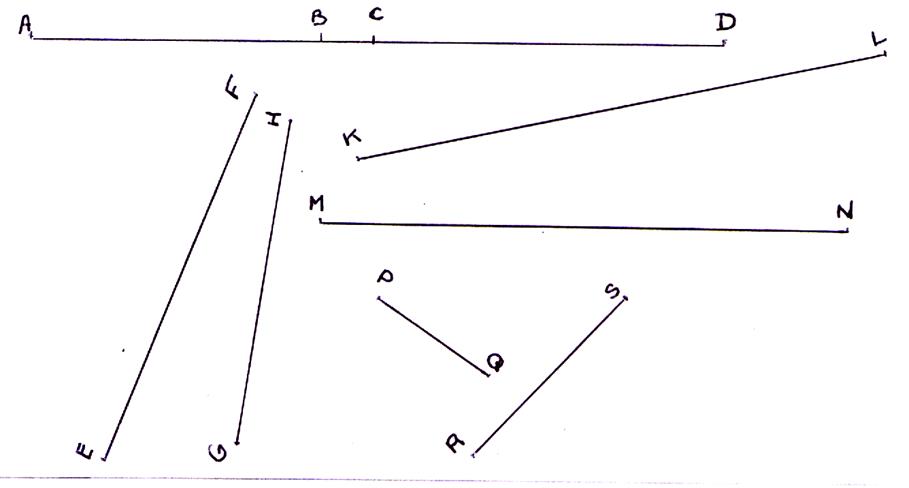
Travaux : graduez
, puis mesurez les segments. |
|
|
A partir du segment unitaire [ OI ] =
1 ; procédure : avec un compas on prend une ouverture égale à la
longueur du segment unitaire (ici OI =
2 cm ) . A partir d’une extrémité du segment on reporte la longueur du segment
unitaire ( tracer un
arc sur la ligne pour obtenir un point d’intersection) .Reporter cette
distance autant de fois qu’il est possible, dépasser l’extrémité si
celle ci ne « tombe » pas juste sur l’arc
du compas . |
|
|
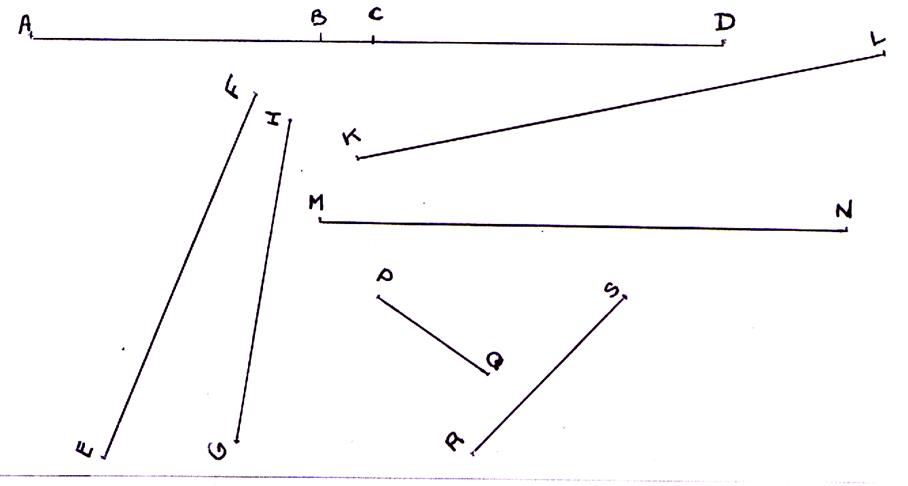
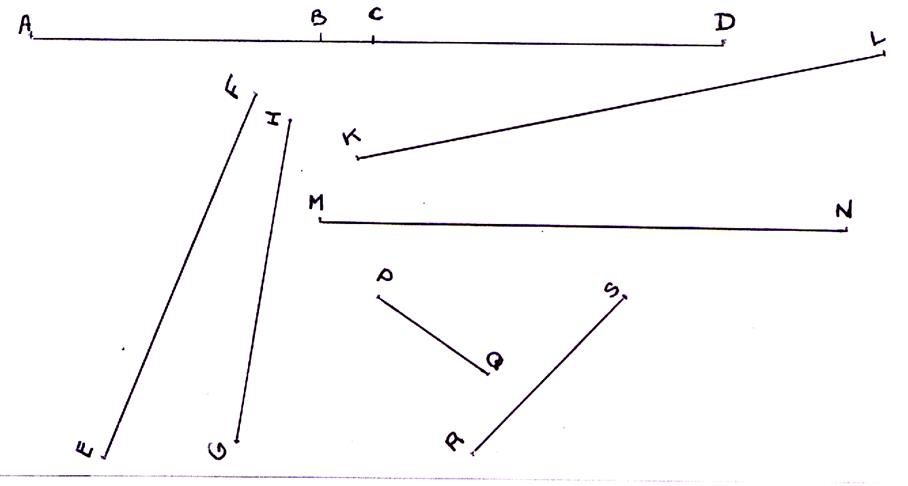
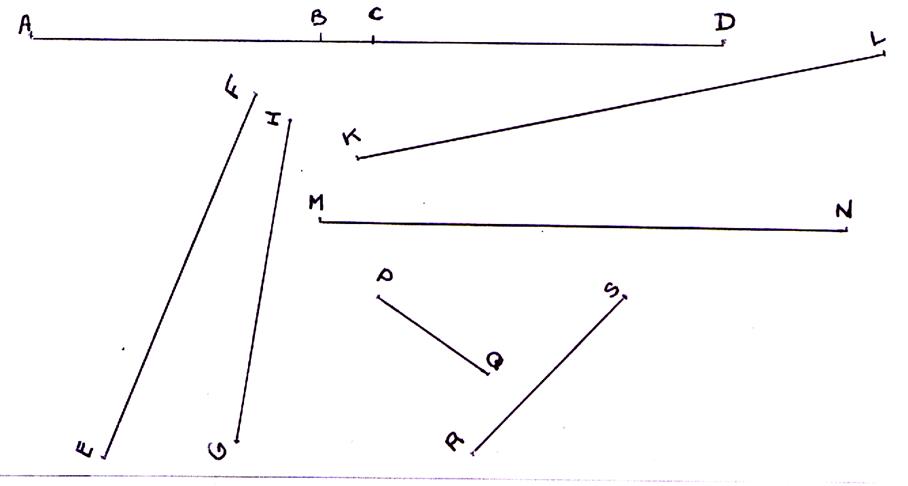
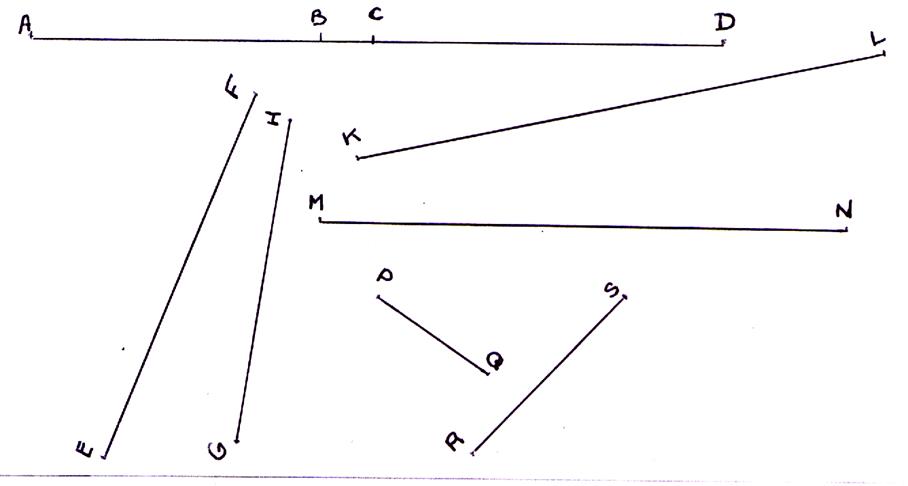
[AB ] ; [BC ] ; [CD ] ; [
EF] ; [GH ] ; [KL ] ; [MN ] ; [PQ ] ; [ RS] ; |
|
|
|
|
|
A ) Mesure
des segments : AB ] = ; [BC ] =
; [CD ] = ; [ EF] = ; [GH ] = ; [KL ] = ; [MN ]
= ; [PQ ] =
; [ RS] = ; [ _ _
] = |
|
|
Graduations : |
|
|
Mesure des segments :
|
Distance |
Commentaire : |
|
[AB ] = entre 2 et 3 |
On est plus prés de 3 ; On peut dire
que le segment vaut « 3 » ; pour
plus de précision il faudrait « fractionner » le segment
, en parts égales. (pour en savoir plus :voir
division d’un segment
) |
|
[BC ] = |
|
|
[CD ] = |
|
|
[ EF] = |
|
|
[GH ] |
|
|
[KL ] |
|
|
[MN ] |
|
|
[PQ ] |
|
|
[ RS] |
|
|
[ _
_ ] |
|
II ) CALCUL de
la DISTANCE
entre deux points sur une droite:
La distance entre deux points est égale à la valeur absolue de la mesure algébrique d ‘un bipoint ( d ’ origine O et d ’extrémité
E ); cette mesure algébrique est égale à
la différence de l ’ abscisse de l’extrémité ( xE )
moins l ‘ abscisse de l ’ origine du bipoint (xO).
Ce qui se traduit :
|
|
½xE
- xO ½= ½ |
|
L'écriture symbolique de la distance entre deux points est : deux lettres majuscules
"ordonnées" surmontées d'un trait horizontal encadrées par une barre
verticale de chaque coté.
|
Procédure : à respecter pour calculer la distance entre deux points. |
Exemple : calculer la mesure algébrique comprise entre les deux extrémités du
segment AB ; avec A(+2) ; B (+7) |
|
Origine du segment: |
XA = (+2) |
|
Extrémité du segment: |
XB = (+7) |
|
Calcul de la mesure algébrique entre les extrémités du segment: |
XA- XB =
(+2) - (+7) Calcul: (+2) - (+7) = (+2) + (-7) = (- (7- 2) ) = (-5) |
|
Détermination de la valeur absolue du calcul précédent : |
½(-5) ½ = 5 |
|
Conclusion |
La distance entre A et B est de 5 |
Exemple
n°2 de problème :
calculer la distance entre les deux points : A (+3) et B (+ 5)
Procédure
:
Il faut
calculer ê![]() ê ( lire :...la
valeur absolue de la mesure algébrique...)avec A (+3) et B (+5)
ê ( lire :...la
valeur absolue de la mesure algébrique...)avec A (+3) et B (+5)
1 ° ) On
pose l'égalité : êx E - x O ê = ê![]() ê
ê
on remplace : ![]() par
par ![]() ;
on repère l’origine et l’extrémité du
bipoint
;
on repère l’origine et l’extrémité du
bipoint
2°) on transforme l'égalité et
on l'adapte en fonction des caractéristiques du bipoint
on obtient : êx B - x A ê = ê![]() ê
ê
on
peut écrire l’ égalité
de cette façon : ê![]() ê = ê x B -
x A ê
ê = ê x B -
x A ê
3° ) on remplace par les valeurs numériques
données :
ê![]() ê = ê (+5) -
(+3) ê
ê = ê (+5) -
(+3) ê
4°) Calcul : (voir :
soustraction de deux nombres relatifs )
ê (+5) - (+3) ê= ê (+5) + (-3) ê
ê (+5) -
(+3) ê= ê ( +
(5 - 3 ) ) ê
ê (+5) -
(+3) ê = ê ( + 2 ) ê
5°) rendre compte : ê![]() ê= ê ( + 2 ) ê
ê= ê ( + 2 ) ê
donc ê![]() ê= 2
ê= 2
TRAVAUX AUTO FORMATIFS.
Série 1 :
Qu'appelle t on
"mesure"
Qu'appelle t on
"longueur "
Qu'appelle t on
"distance"
Pour quoi est
utilisée la mesure algébrique ?
Série
2 :
1° )A quoi est égale
la distance entre deux points ? …………………………………
2°)Traduire en
langage littéral : ½xE - xO ½= ½![]() ½ ; que cherche t - on à connaître ?
½ ; que cherche t - on à connaître ?
3 °) Traduire en langage mathématique :
La distance entre deux point est égale à la
mesure algébrique d ‘un bipoint ( d ’ origine B et d ’extrémité A ) qui elle est égale
à la différence de l ’ abscisse de l’extrémité A moins l ‘ abscisse de l ’ origine du bipoint
B.
4°) Donnez la procédure pour calculer la
distance entre deux points .
Graduation et mesure
(distance)d’un segment :
Ce travail propose 4 travaux différents ;
éventuellement voir ( INFO :
SOS graduation )
et ( INFO :
SOS mesure) ; (INFO mesure d’un segment)
|
Série 1 : |
|
|
à
partir du segment unitaire [ OI ] = 1 ;
donner le mesure des segments : |
|
|
[AB ] ; [BC ] ; [CD ] ; [ EF] ; [GH
] ; [KL ] ; [MN ] ; [PQ ] ; [ RS] ; |
|
|
|
|
|
A ) Mesure
des segments : AB ] = ; [BC ] =
; [CD ] = ; [ EF] = ; [GH ] = ; [KL ] = ;
[MN ] =
; [PQ ] = ; [ RS] = ; [ _ _ ] = |
|
|
Série 2 : |
|
|
à
partir du segment unitaire [ OI ] = 1 ;
donner le mesure des segments : |
|
|
[AB ] ; [BC ] ; [CD ] ; [ EF] ; [GH
] ; [KL ] ; [MN ] ; [PQ ] ; [ RS] ; |
|
|
|
|
|
A ) Mesure
des segments : AB ] = ; [BC ] =
; [CD ] = ; [ EF] = ; [GH ] = ; [KL ] = ;
[MN ] =
; [PQ ] = ; [ RS] = ; [ _ _ ] = |
|
|
Série 3 : |
|
|
à
partir du segment unitaire [ OI ] = 1 ;
donner le mesure des segments : |
|
|
[AB ] ; [BC ] ; [CD ] ; [ EF] ; [GH
] ; [KL ] ; [MN ] ; [PQ ] ; [ RS] ; |
|
|
|
|
|
A ) Mesure
des segments : AB ] = ; [BC ] =
; [CD ] = ; [ EF] = ; [GH ] = ; [KL ] = ;
[MN ] =
; [PQ ] = ; [ RS] = ; [ _ _ ] = |
|
|
Série 4 : |
|
|
à partir
du segment unitaire [ OI ] = 1 ; donner
le mesure des segments : |
|
|
[AB ] ; [BC ] ; [CD ] ; [ EF] ; [GH
] ; [KL ] ; [MN ] ; [PQ ] ; [ RS] ; |
|
|
|
|
|
A ) Mesure
des segments : AB ] = ; [BC ] =
; [CD ] = ; [ EF] = ; [GH ] = ; [KL ] = ;
[MN ] =
; [PQ ] = ; [ RS] = ; [ _ _ ] = |
|
CALCULS
Exercice n° 1:
Enoncé :
Calculer d (A,B
) avec A (+3) et B (+5)
Donner les deux solutions : Le graphique
et par le calcul.
Exercice n°2 :
Enoncé :
Calculer d(A,B)
avec A (+3) et B (-5)
Donner les deux solutions :graphique et par le calcul.
|
Cliquez
ici pour : |