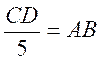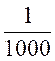multiplication la longueur du segment

La division dans N

Index  warmaths

Objectif précédent : conversions de longueur    

Objectif suivant :

1°): la division décimale

2°) la fraction de longueur

tableau 

2°) les opérations sur les longueurs

DOSSIER : Division de longueur (segment).

I )Division d’une longueur par un nombre :

II ) QUOTIENT D’UNE LONGUEUR PAR UN NOMBRE :

III )   Recherche du QUOTIENT APPROCHE D’UN NOMBRE QUELCONQUE par un NOMBRE  ENTIER ou DECIMAL :

IV ) ETUDE des CAS ou le DIVIDENDE N’EST PLUS UN NOMBRE ENTIER.

TEST

COURS

Devoir  Contrôle

Devoir évaluation

1°)Interdisciplinarité

     2°)Série2

Corrigé Contrôle 

Corrigé évaluation 

COURS

I ) Division d’une longueur par un nombre :

Rappel :

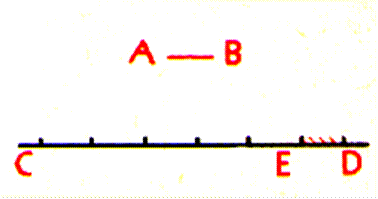
Nous avons vu que dans la multiplication la longueur du segment CD est égal  à :

CD = 5 AB

Inversement , nous pouvons partager la longueur CD en 5 longueurs égales à AB ; nous disons que la longueur AB est le quotient de la longueur CD par 5 :

Nous l’écrivons : 

 CD : 5 = AB

Le signe « : » se lit « divisé par … »

Donc calculer la longueur AB revient à calculer l’un des facteurs d’un produit connaissant ce produit : CD et l’un des facteurs de ce produit « 5 »

La longueur CD est le dividende .

Le facteur connu « 5 » est le diviseur

. remarque : pour indiquer que AB est le quotient de CD , par 5 , on peut encore employer la notation :

Exercice 1 :

La longueur d’un segment CD est égale à 15 cm. Trouver la longueur du segment AB.(CD contient 5 fois le segment AB)

Cette longueur doit être telle qu’en la multipliant par 5 nous retrouvions 15 cm.

La longueur cherchée est 3 cm , en effet :  15 = 5  3

Exercice 2 : la longueur du segment CD étant égale à 17 cm , trouver la longueur du segment AB.

Il n’existe pas  de nombre entier qui multiplié par 5 donne 17 , si nous voulons partager  CD en 5 segment égaux de façon que chacun d’eux mesure un nombre entier de centimètres , il faut une longueur de 3 cm , il reste sur le segment CD une longueur de  2 cm inutilisé.

L’examen de la figure nous permet d’écrire :

CD = 5 AB + ED ou

17 = 5   3 + 2

Voir “division euclidienne”:

II )   QUOTIENT D’UNE LONGUEUR PAR UN NOMBRE :

Commentaire : ce chapitre permet d’expliquer la division euclidienne .

                  Le quotient d’une longueur appelée « dividende » , par un nombre appelé « diviseur » , est la plus grande longueur dont le produit par le diviseur est inférieur ou égal au dividende.

Cette définition peut s’appliquer à une grandeur quelconque : surface , volume , poids , capacité .

                  Dividende = diviseur  quotient + reste

Deux cas peuvent se présenter :

Si le reste de la division est nul , le quotient est dit « exacte » ;      Voir exercice 1 ;  « 3 » est le quotient exacte de 15 par 5

Si le reste n’est pas nul , le quotient est approché. ;       Voir exercice 2 ;  « 3 » est le quotient approché de 17 par 5

La division est l’opération qui permet de trouver un quotient.

Remarques :

1)   La division par 0 n’a pas de sens

2) Le reste d’une division doit toujours être inférieur au diviseur

3) Dans les deux exercices précédents , nous connaissons le nombre de parts  et nous avions à calculer la valeur d’une part ; le dividende et le quotient étaient exprimés avec la même unité.

On peut avoir à calculer le nombre de parts connaissant la valeur de chacune d’elles :

Exemple : un galon a 72 cm de longueur , on veut le partager en plusieurs morceaux ayant chacun pour longueur 8 cm .

Calculer le nombre de morceaux.

Résolution :

Le nombre de morceau doit être tel que son produit par 8 soit égal à 72 , ce nombre est « 9 » :  72 : 8 = 9

Ici , le dividende et le diviseur sont de même nature , le quotient qui représente un nombre de parts est de nature différente.

Pratique de la division :

Recherche du quotient entier d’un nombre entier par un nombre entier.

Premier Cas.

Le diviseur et le quotient n’ont qu’un chiffre : 85 : 9

Le quotient est plus petit que 10 car 910 >85

La connaissance  de la table de multiplication permet de

Trouver ce quotient :  85 : 9 = 9  le reste est « 4 »

Deuxième cas

Exercice :      soit à partager une pièce d’étoffe ayant 174 m de longueur en 25 coupons d’égale longueur . (sans décimales )

Longueur de chaque coupon :  174 m : 25

Le diviseur est un nombre entier quelconque , le quotient n’a qu’un chiffre.

Le quotient est plus petit que 10 car : 25 10 > 174

Supposons que l’on ne veuille avoir que 20 coupons. Si chacun de ces coupons a 1 mètre de longueur  , on utilise  20 mètres de la pièce  ou encore 2 décamètres. Donc autant de fois  2 dam sont contenu dans 17 dam , autant de fois on peut donner à chaque coupon une longueur de 1 mètre :

17 : 2 = 8 .

Mais en réalité nous avons  25 coupons.

Il faut donc voir si le produit de 8 par 25 est inférieur ou égal à 177 :

825 = 200  or 200 > 174 , donc 8 ne convient pas !

essayons  7 :

7  25 = 175 or  175 > 174 ; donc 7 ne convient pas encore !

essayons  6 :

6  25 = 150       150 < 174 ; 6 convient , donc la longueur d’un coupon est égal à 6 mètres.

On peut poser l’opération ainsi :

       17 dam   4 m      25

     - 15 dam   0 m        6 m

        2 dam    3 m

    ou            23 m

Ou plus simplement

175        25

  23     6

Conclusion :    174 m : 25 = 6 m      il reste 23 m

Troisième cas

Exercice : un grossiste a réparti 1 735 mètres de tissus entre 25 détaillant , de façon que chacun d’eux ait la même quantité.

Calculer la longueur d’ étoffe reçue.

Longueur d’étoffe  reçu par chaque détaillant : 1735 m : 25

Le diviseur et le quotient sont des nombres entiers quelconque.

Le quotient cherché est compris entre  10 et 100 , en effet :

25 10  < 1735

25 100 > 1 735

le quotient a donc deux chiffres : la longueur cherchée est donc formée d’un certain nombre de décamètres et d’un certain nombre de mètres  .

le nombre de décamètres s’obtient en divisant le nombre de décamètres 1735 mètres par 25 , nous savons le calculer :

puisqu’il y a 173 dam dans la longueur donnée  , ce quotient est égal à 6.

Si le grossiste ne distribue que 6 dam à chacun des détaillants , il distribue en tout 150 dam ou 1500m et il lui reste encore 235 mètres  à distribuer, le quotient de 235 par 25 étant égal à 9 , chaque détaillant peut recevoir un supplément de 9 m . En définitive , la longueur cherchée se compose de  6 dam et 9 m  , soit 69 m

L’opération peut se poser ainsi :

               173 dam  5m     25

               150 dam            6 dam 9 m

                 23 dam 5 m

                    ou  235 m

                          225 m

                 reste    10 m

Ou plus simplement

1 735     25

   235      69

    10

III )   Recherche du QUOTIENT APPROCHE D’UN NOMBRE QUELCONQUE par un NOMBRE  ENTIER ou DECIMAL :

Pré requis

Rappel : nous savons calculer le quotient entier approché dans le cas où le dividende et le diviseur sont des nombres entiers.

Exemple : 2 cm est le quotient entier approché de 17 cm par 6 , parce que  2 cm représente le plus grand nombre de centimètres dont le produit par 6 est contenu dans 17 cm ; 3 cm ne convient pas puisque :

                    3 cm 6 >17 cm

On dit encore que :

 2 cm est le quotient à une unité prés par défaut de 17 cm par 6 .

3 cm est le quotient à une unité près par excès de 17 cm par 6.

Si nous calculons le reste de la division , dans le premier cas nous trouvons 5 cm ; mais nous pouvons essayer de calculer le quotient avec une plus grande approximation :

La longueur qui reste , 5 cm   ou 50 mm , peut être divisée à son tour en 6 parties égales ayant chacune pour longueur  8 mm  ( 8 est en effet  le quotient à une unité près de 50 par 6 et il reste  2 mm) si nous ajoutons ces 8 mm aux 2 cm précédemment trouvés , nous dirons que :

2,8 cm est le quotient à 1 mm prés ou encore à près de 17 cm par 6.

Nous pouvons du reste nous contenter de cette approximation et nous posons ainsi l’opération :   17      6

                                                             50     2 , 8

                                                               2 

remarque : le reste représente ici  des dixièmes de centimètre  ou encore 2mm

IV ) ETUDE des CAS ou le DIVIDENDE N’EST PLUS UN NOMBRE ENTIER.

Voir   « la division décimale »

Preuve de la division : 2 procédés