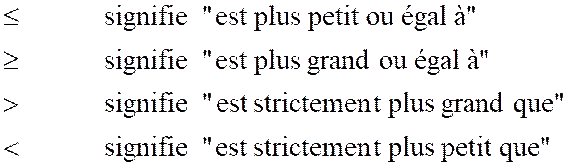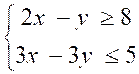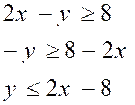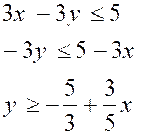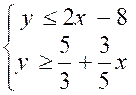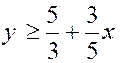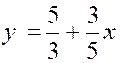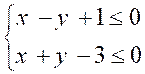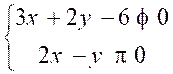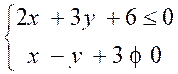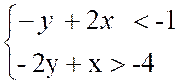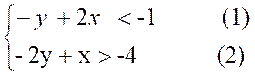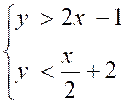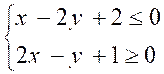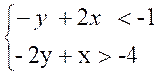Pré
requis:
|
Régionnement et inégalité des distances
(5ème)
|

|
|
Système d’équation du premier degré à une inconnue
|

|
|
Résolution de l’équation du premier degré à deux inconnues
|

|
|
Fonction linéaire (représentation graphique)
|

|
|
Fonction affine (représentation graphique)
|

|
ENVIRONNEMENT du dossier:
DOSSIER : LES INEQUATIONS du premier degré
et du second degré.
Les systèmes
d’équations . (niveau IV )
|
TEST

|
COURS

|
Devoir Contrôle 
|
Devoir évaluation 
|
Interdisciplinarité

|
|
Corrigé Contrôle 
|
Corrigé évaluation

|
I )
INEQUATIONS A UNE INCONNUE DU PREMIER DEGRE
¶
Définition
Une inéquation est
une relation d'ordre mathématique qui comprend une inconnue en général notée x.
Elle comprend les sigles suivants :
· Elle est du premier
degré lorsque la puissance de « x » ne dépasse pas 1
·
Elle
est du second degré lorsque la puissance
de « x » est de « 2 » .
Résoudre une
inéquation :
Résoudre une inéquation, c'est
trouver toutes les valeurs de l'inconnue pour que l'inéquation soit vérifiée.
Ces valeurs sont les solutions
de l'inéquation.
Exemple : Résoudre l’inéquation
|
4x - 1
|
>
|
x + 2
|
|
premier
membre
|
|
second
membre
|
·
Si
x = 0, alors le premier membre vaut:
4 ( 0 )
- 1 = ( 0 ) - 1 = -1 et le second membre
vaut: 0 + 2 = 2.
Comme -1 > 2 est faux, alors 0 n'est pas solution de l'inéquation.
·
Si
x = 3, alors le premier membre vaut: 4 * 3 - 1 = 12 - 1 = 11
et le second membre vaut: 3 + 2 = 5.
Comme 11 > 5 est vrai, alors 3 est une solution de l'inéquation.
On remarque qu'il y a
une infinité de solutions possibles. On parlera donc d'ensemble de solutions.
Pour trouver les
solutions d'une inéquation, la méthode suivante est utilisée.
· Méthode de résolution
Objectif : "Isoler
x" dans un membre (généralement le premier membre).
Procédé : Transformer
l'inéquation à l'aide des règles 1 ,2 et 3 énumérées ci
après.
Une inéquation a les
mêmes solutions que toutes les inéquations obtenues:
·
R1: En ajoutant ou en
retranchant un même nombre aux deux membres de l'inéquation:
Si
a < b alors a + c < b +
c (ex: a + 5 < b + 5)
alors
a - c < b - c (ex: a - 5 < b - 5)
· R2:
En multipliant ou en divisant par un même nombre positif non nul les
deux membres de l'inéquation:
Si
a > b et c >
0 alors a * c > b *
c (ex: a * 3 > b * 3)
alors
a / c > b / c (ex: a / 3 > b / 3)
·
R3: En multipliant ou en
divisant par un même nombre négatif non nul les deux membres de
l'inéquation et en changeant le sens de l'inégalité:
Si
a > b et c <
0 alors a * c < b *
c (ex: a * (-4) < b * (-4))
alors
a / c < b / c (ex: a / (-4) < b / (-4))
Exemple :
Résoudre
l'inéquation : 4x - 1 > x + 2
• On regroupe les
"termes en x" dans le premier membre à l'aide de R1: (on retranche
x)
4x
- 1 - x > x + 2 - x
On réduit : 3x - 1 >
2
• On regroupe les
"termes sans x" dans le second membre à l'aide de R1: (on ajoute
1)
3x
- 1 + 1 > 2 + 1
On réduit :
3x >
3
• On "isole
x" à l'aide de R2: (on divise par 3 dans les deux membres)
3x
/ 3 > 3 / 3
On réduit : x >
1
Conclusion : Les solutions sont
tous les nombres strictement plus grand que 1.
On note également
l'ensemble des solutions sous la forme d'un intervalle dans ce cas cet
intervalle est : ] 1 ;
+ ¥
[ ; ( "+ ¥
" se lit "plus l'infini", ce sont tous les nombres positifs très
grands ).
* Précisions
sur la notations des intervalles de nombres :
[ 2
; 5 ] : intervalle 2 ; 5 fermé ce sont
tous les nombres x tels que : 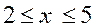
[ 2
; 5 [ : intervalle 2 fermé ; 5 ouvert ce sont tous les nombres x tels que : 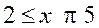
] 2 ; 5 [ : intervalle 2 ; 5 ouvert, ce sont tous les nombres x tels que
: 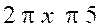
] - ∞ ; 2 ] : ce sont tous les nombres x tels que 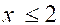
] - ∞ ; 2 [ :
ce sont tous les nombres x tels que : 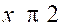
[ 2
; + ∞ [ : ce sont tous les nombres x tels que : 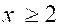
] 2 ; + ∞ [ :
ce sont tous les nombres x tels que : 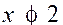
+Exercice
n°1
Donner les solutions
des inéquations suivantes sous forme d'intervalle :
5x
+ 2 > -x -4 3x + 8
> 5 -4x + 2 > 0 7x -4 < 18
II ) INEQUATIONS A UNE INCONNUE DU SECOND DEGRE
Ces
inéquations se ramène à l'étude du signe du polynôme ax² + bx
+ c. Pour mémoire ( voir cours sur les équations et polynômes du second degré ) :
¶
Si le polynôme n'a pas de solutions, alors pour tout réel x, le polynôme est du
signe de « a »
·
Si le polynôme a une ou deux solutions, alors on effectue la factorisation du
polynôme et on construit un tableau de signe.
Exemple : Résolution
de 15x²-17x-4 < 0
L'équation 15x²-17x-4 = 0 admet deux
solutions -1/5 et 4/3 donc :
15x²-17x-4
= 15(x+1/5)(x-4/3)
L'inéquation se ramène donc à 15(x+1/5)(x-4/3)
< 0
Il faut donc étudier le signe du produite
(x+1/5)(x-4/3)
On fait un tableau de signe :
|
Valeurs
de x
|
-1/5 4/3
|
|
Signe
de x+1/5
|
- 0 +
|
|
Signe
de x-4/3
|
- 0 +
|
|
Signe
de (x+1/5)(x-4/3)
|
+ 0
- 0 +
|
|
Signe
de 15x²-17x-4
|
+ 0 -
0 +
|
D'après le tableau de signe l'ensemble
solution de cette inéquation est ] -1/5 ; 4/3 [
+Exercice
n°2
Résoudre les inéquations suivantes :
-2x²+3x+8 > 0 4x²+8x+15 > 0 13x² - 2x + 5 > 0
III )
SYSTEMES D'INEQUATIONS A DEUX INCONNUES
Un système de 2 inéquations à deux inconnues x et y est
tel que : 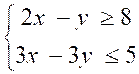
Résoudre un tel système consiste à trouver toutes
les valeurs de x et y qui vérifient à la fois les deux inéquations.
Pour résoudre un tel
système on utilise une méthode graphique.
On exprime les deux
inéquations en isolant y dans un membre :
Inéquation n°1 :
on transforme
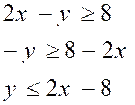
Inéquation n° 2 : on transforme
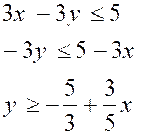
Le système 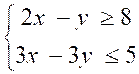 est donc équivalent
à :
est donc équivalent
à : 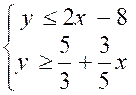
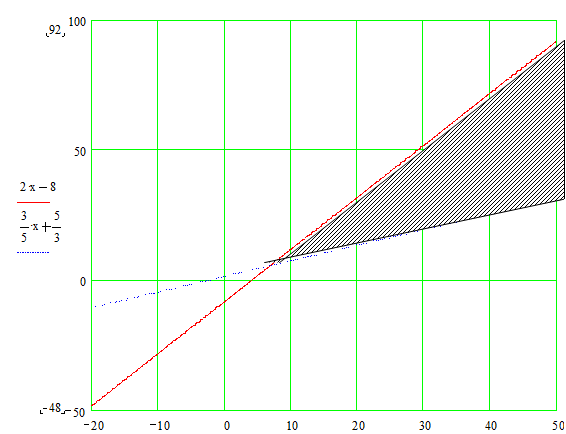
Dans le cas où y = 2x - 8 l'ensemble des couples
solutions (x ; y) sont graphiquement
situés sur la droite d'équation y = 2x - 8.
Ainsi l'ensemble des
solutions de l'inéquation 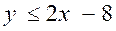 est constitué par
l'ensemble des points dont les coordonnées sont situés
au dessous de la droite d'équation y = 2x - 8
est constitué par
l'ensemble des points dont les coordonnées sont situés
au dessous de la droite d'équation y = 2x - 8
De la même façon, les
solutions de l'inéquation 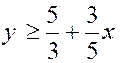 sont situés au dessus de la droite d'équation
sont situés au dessus de la droite d'équation 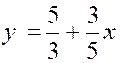 .
.
Les solutions du
système 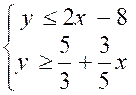
sont donc constituées
des coordonnées (x ; y ) des points situés à l'intersection des zones
énumérées ci-dessus.
Cela se traduit donc
graphiquement par la zone hachurée ci-dessous :
On constate donc graphiquement que cette zone commence au
point d'intersection des deux droites.
+Exercices n°3
Résoudre
graphiquement les systèmes d'inéquations proposés. Colorier les zones solutions
des systèmes.
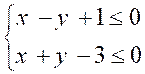
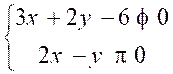
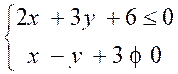
|
Autre exemple de résolution d’un SYSTEME avec 2 INEQUATIONS :
|
Par définition : la donnée simultanée de deux (ou plusieurs)
inéquations s’appelle un « système d’inéquations ».
Résoudre un système d’inéquations :
c’est chercher toutes les solutions « communes » aux
inéquations.
Application 2:
On demande
de résoudre graphiquement le système : 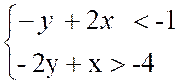
|
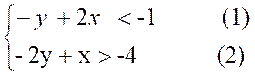
Transformations :
On
transforme (1) y >2 x -1
On
transforme (2)
-2y > -x - 4
Û 2y < x
+ 4 soit y < 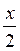 +2 +2
· Ï le système devient : 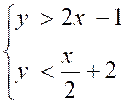
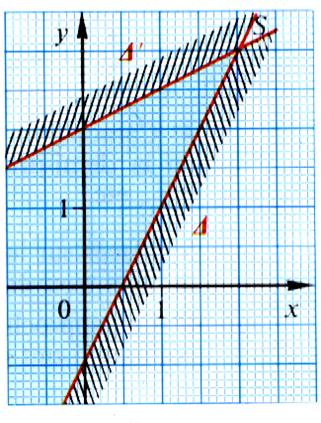
· On trace les droites :
 d’équation : y = 2x -1 d’équation : y = 2x -1
et
 ’ d’équation :
y’ = ’ d’équation :
y’ = 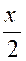 +2 +2
|
|
Pour chaque
inéquation on considère le demi plan qui convient (on considère le point
origine O (0 ;0) ; on cherche si il
appartient ou pas au demi plan )
La solution
graphique du système correspond à tous les points communs aux deux demi plans
(zone non barrée)
Remarques :
les droites 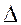 et
et 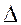 ‘ sont sécantes au point de coordonnées ( 2 ;3) ; Ce point
n’est pas solution du système. ( parce que nous
avons des inégalités strictes)
‘ sont sécantes au point de coordonnées ( 2 ;3) ; Ce point
n’est pas solution du système. ( parce que nous
avons des inégalités strictes)
Application
3 :
|
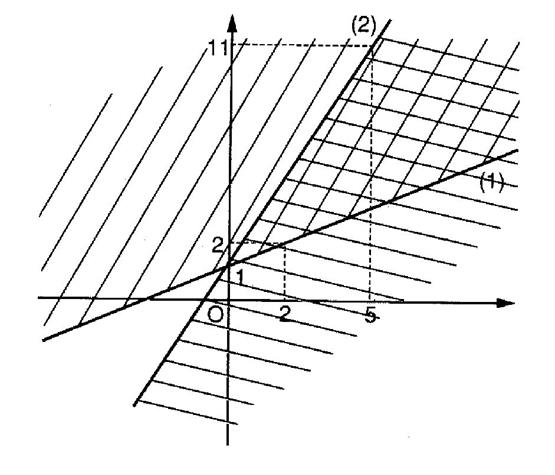
On demande de résoudre le système suivant :
|
Solution graphique :
Vous
remarquerez que la partie du plan non hachurée est solution, ainsi que les
deux droites, car les inégalités sont données au sens large.
|
|
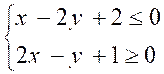
|
|
TRAVAUX AUTO FORMATIFS.
CONTROLE :
EVALUATION
A)
|
Résoudre graphiquement les inégalités suivantes :
|
|
|
|
|
|
x
- 2y + 4 > 0
|
(corrigé dans le cours)
|
|
|
|
|
y – 3 > x -5
|
|
|
|
|
|
2x – 5 > x + 4
|
|
|
|
|
|
2y - 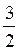 < x + < x + 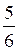
|
|
|
|
|
|
- 4y + 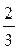 > > 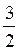 x + 4 x + 4
|
|
B)
Résoudre le système suivant :
|
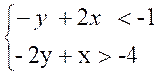
|
Corrigé
dans le cours.
|