Pré requis:

Lecture : L'algèbre
Lecture : l'arithmétique .

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent :

Les égalités (vocabulaire)

Objectif suivant

1°) Les égalités ( sommaire )

2°) Les égalités et « résoudre »

3°)résolution des équations types du premier degré à une inconnue.

Liste des cours en algèbre.

DOSSIER : L ‘ EQUATION

I ) « EQUATION » et « IDENTITE » (définitions)
II) RESOUDRE d’une équation.
a) Résolution algébrique	Exemples d’exercices « résoudre »
b) Résolution graphique

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

COURS

I ) DEFINITIONS : ( des mots et expressions utilisés) en algèbre

IDENTITE :

On appelle « identité » une égalité évidente ou une égalité satisfaite quelles que soient les valeurs numériques des lettres qui y entrent.

Ainsi

Est une identité : 8 = 8

( a + b )² = a ² + 2ab + b² est aussi une identité

Par contre l’ égalité : 5 x = 40

N’est pas une identité , car si nous remplaçons « x » par 3 , par exemple , le membre de gauche est égal à 5 fois 3 soit « 15 » , le membre de droite est égal à 40 ; et 15 n’est pas égal à 40 .

Si je remplace « x » par 8 , le membre de gauche est égal à 40 , et par conséquent l’égalité se transforme en identité : 40 = 40

L’égalité 5x = 40 ne se réduit donc à une identité que si l’on remplace « x » par une valeur convenablement choisie , c’est une équation.

%Ä Info sur les égalités (Déf.)

EQUATION :

On appelle « équation » une égalité qui n’ a lieu que pour certaines valeurs attribuées à une ou à plusieurs lettres appelées « inconnues »

On appelle « équation » une égalité qui ne se réduit à une identité que pour des valeurs particulières des lettres qui y entrent.

Exemples : 5x = 40 ; y = 2x +4 ; 2y = x² + x ; -5x +7 = x +5 ; ……

Toute équation est de la forme A = B

« A » est le premier membre de l’équation et « B » le second membre.

Une équation est une phrase interrogative : l’équation 5x = 21 , dont l’inconnue est notée « x » , est la question : « Pour quelles valeurs numériques de « x » , l’égalité 5x = 21 est - elle vraie ? » « x » = 4,2 est la réponse à la question , on dit que « 4,2 » est la solution de l’équation .

L’activité qui consiste à Rechercher la valeur de « x » qui vérifie l’égalité « vraie » s ‘ appelle : résoudre.

Inconnues

Les lettres qu’il faut remplacer par des valeurs particulières pour obtenir une identité sont les inconnues de l’équation ; on les désigne généralement par les lettres « x » « y » ; « z » ; « t » ; « u ».

Exemples :

5x + 7 = 6x +13 est une équation à une inconnue.

2x + 5 y - 3 = 4x -3y + 2 est une équation à deux inconnues

SOLUTIONS ou RACINES

Les valeurs particulières qu’il faut donner aux inconnues pour avoir une identité sont appelées « les solutions » ou « racines » de l’équation.

On appelle « solution » d’une équation tout ensemble de nombre qui , mis à la place des inconnues , donne aux deux membres la même valeur.

Dans le cas d’une équation à une inconnue, une solution est également appelée « racine » de l’équation.

Ainsi l’équation 5x + 7 = 6x +13 admet la racine « x = - 6 » parce que pour « x » = -6 les deux membres sont égaux à « -23 ». On dit encore que pour « x » = -6 l’équation est « satisfaite ».

« Résoudre une équation » , c’est trouver ses solutions.

Mais pour résoudre une équation, on la transforme en équations « équivalentes » jusqu’à ce que l’on obtienne une équation dont la résolution est immédiate.

Exemple c’est en transformant l’équation 5x + 7 = 6x +13 que l’on soit arrivé à l’équation « immédiate » x = - 6

Pour cela, on utilise certains théorèmes , que nous avons déjà vu dans les travaux sur les égalités.

EQUATION SATISFAITE ou VERIFIEE

On dit qu’une équation est satisfaite ou vérifiée pour les valeurs des inconnues qui sont racines.

L’égalité 5x = 40 ne se réduit donc à une identité que si l’on remplace « x » par une valeur convenablement choisie , c’est une équation . « 8 » vérifie l’équation ; pour trouver la valeur « 8 » on a fait une activité mathématique appelé « résoudre » .( on fait 40 : 5 )

II ) RESOUDRE UNE EQUATION

Il y a deux possibilités de résoudre une équation : algébriquement ou graphiquement.

a) RESOLUTION ALGEBRIQUE

Résoudre : c’est trouver ses solutions.

« Résoudre une équation » c ' est rechercher la valeur de l ' inconnue (appelée généralement " x " ) qui vérifie que l ' égalité est vraie.

Exemples d’équations.	Résoudre c'est : ….	justification
2+ x = 5	Résoudre c'est rechercher la valeur de "x" ,qui ajoutée à 2 donne la valeur "5"	Ici "x" vaut "3" ; parce que "2" plus "3" égale "5"
2 x = 6	Résoudre c'est rechercher la valeur de "x" ,qui multipliée à 2 donne la valeur "6"	Ici "x" vaut "3" ; parce que "2" fois "3" égal "6"
x - 2 = 5	Résoudre c'est rechercher la valeur de "x" ,à qui l'on soustrait 2 donne la valeur "5"	Ici "x" vaut "7" ; parce que "7" moins "2" égal "5"
x : 2 = 3	Résoudre c'est rechercher la valeur de "x" ,qui divisée 2 donne la valeur "3"	Ici "x" vaut "6" ; parce que "2" fois "3" égal "6" ; donc "6" divisé par "2" égal "3"
Autre exemple : 2 x + 12 = 17 il faut transformer !	2 x + 12 = 17 2x = 17-12 2x = 5 x = 5: 2 x = 2,5	2 fois 2,5 + 12 = 5 + 12 = 17 donc "x" vaut 2,5

On peut résoudre des équations du premier degré ; du second degré et d’autres encore.

Donc « résoudre » ; c'est avoir une égalité contenant une lettre appelée « inconnue » et dont on voudrait connaître la valeur numérique . et pourvoir vérifier que la valeur trouvée réalise "l'égalité vraie " proposée.

Cette lettre se trouve être un facteur « intégrer » dans un terme.

(par exemple : si on donne « 3x =5 » ;

3x : « 3 » et « x » sont des facteurs du terme du premier membre).

Résoudre : c’est isoler « x » dans le premier membre de l’égalité.

Pour régler le problème de la résolution d'une équation il faut se poser la question :

Quelle peut être la valeur de "x" qui vérifie l'égalité ?

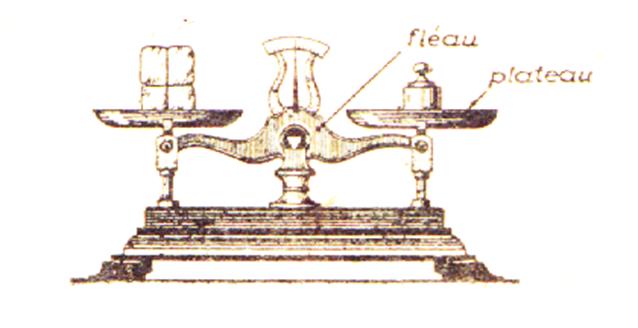
L'outil utilisé pour comprendre la transformation d'une égalité est la balance de Roberval. (étalonnée au « 0 »)

roberval

L’égalité doit rester vraie , on doit toujours après transformation obtenir le maintien de l’aiguille à « 0 ».(on imagine que pour conserver l’ équilibre : on ajoute autant , on divise autant , on retranche autant , on multiplie autant dans chaque plateau )

Il est donc nécessaire de connaître les règles (théorèmes) qui permettent de transformer une égalité ! ! ! ! ! !.

Théorèmes @ SOS cours

Transformer une égalité : c'est mettre les "x" dans le premier membre de l'égalité et les nombres et opérations associées dans le deuxième membre de cette égalité

Et ensuite par un calcul approprié (généralement une division ) on doit trouver une valeur numérique que l'on affecte à "x" .

Il faut bien entendu vérifier : c'est à dire remplacer dans l'égalité de départ "x" par la valeur "trouvée" , si l'on trouve deux nombres identiques pour chaque membre , on conclut que la valeur de "x" trouvée est " solution de l'équation" ;sinon cela signifie que l' on a fait une erreur dans les transformations , il faudra donc reprendre au "départ" et rechercher une autre proposition pour qu'elle puisse être solution .

b) RESOLUTION GRAPHIQUE

Info @

La résolution graphique.

En général on trace des points dans un repère , souvent :cartésien.

Chaque point possède des coordonnées.

L’ensemble des points forment soit une droite soit une courbe ( parabole ; hyperbole ;……)

Voir les représentations graphiques ;…… Info @

TRAVAUX AUTO FORMATIFS.

CONTROLE :

1. Donner la définition de : IDENTITE :

2. Donner la définition de : EQUATION :

3. Donner la définition de : Inconnues

4. Donner la définition de : SOLUTIONS ou RACINES

5. Que signifie : EQUATION SATISFAITE ou VERIFIEE ?

EVALUATION

Aucune évaluation.

INTERDISCIPLINARITE

CORRIGE du CONTROLE.

Donner la définition de : IDENTITE :

On appelle identité une égalité évidente ou une égalité satisfaite quelles que soient les valeurs numériques des lettres qui y entrent.

Donner la définition de : EQUATION :

On appelle « équation » une égalité qui ne se réduit à une identité que pour des valeurs particulières des lettres qui y entrent.

Donner la définition de : Inconnues

Les lettres qu’il faut remplacer par des valeurs particulières pour obtenir une identité sont les inconnues de l’équation ; on les désigne généralement par les lettres « x » « y » « z » « t » « u ».

Donner la définition de : SOLUTIONS ou RACINES

Les valeurs particulières qu’il faut donner aux inconnues pour avoir une identité sont appelées « les solutions » ou « racines » de l’équation.

Que signifie : EQUATION SATISFAITE ou VERIFIEE ?

On dit qu’une équation est satisfaite ou vérifiée pour les valeurs des inconnues qui sont racines.