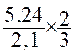Retour vers tous les cours de collège

Pré requis : programme 6^ème

Niveau Suivant : 4^ème

	MATHEMATIQUES - FORMATION COLLEGE
>>>Retour index warmaths .		Vers les listes des cours de collège..

Collège: 5^ème

Ø Liste d’explication des contenus et Définitions des « objectifs - compétences » .
	A chaque compétence doit correspondre un objectif. A chaque objectif doit correspondre : une leçon  + un devoir ( à réussir ) de contrôle ( savoirs ) et d’évaluation ( savoir-faire ).	Voir notation du devoir formatif .
1°) Compétences en TRAVAUX GEOMETRIQUES
2°) Compétences en TRAVAUX NUMERIQUES :
3°) Compétences en ORGANISATION ET GESTION DE DONNEES , FONCTIONS

Lire 1: des nombres et des grandeurs

Lire 2 : mesure des grandeurs

Explicitations des contenus de la classe de 5^e :

Le professeur a toute liberté dans l’organisation de son enseignement à condition que soient atteints les objectifs visé par le programme.

1°) TRAVAUX GEOMETRIQUES

En classe de 6^e , les élèves ont été progressivement habitués à s’exprimer d’une manière précise pour décrire des figures et mettre en œuvre de courtes séquences déductives.

En classe de 5^e  ;l’étude des figures se poursuit. Un nouvel outil , la symétrie centrale permet d’enrichir et de réorganiser les connaissances sur les figures , dont certaines propriétés pourront être démontrées ; : le parallélogramme est une figure fondamentale du programme . Dans l’espace , les études expérimentales s’amplifient ; elles fournissent un terrain pour dégager quelques propriétés élémentaires du parallélisme et de l’orthogonalité .

Les travaux de géométrie plane prennent toujours appui sur des figures , dessinées suivant les cas à main levée ou à l’aide des instruments de dessin et de mesure , y compris dans un environnement informatique . Ils sont conduits en liaison étroite avec l’étude des autres rubriques ; ils constituent en particulier , le support d’activités numériques conjointes ( grandeurs et mesures ) . Les diverses activités de géométrie habitueront les élèves à expérimenter et à conjecturer , et permettront progressivement de s’entraîner à des justification au moyen de courtes séquences déductives mettant en œuvre les outils du programme et ceux déjà acquis en 6^e , notamment la symétrie axiale , il importe de faire peu à peu percevoir aux élèves ce qu’est l’activité mathématique , tout en veillant à ne pas leur demander de prouver des propriétés perçues comme évidentes.

Contenus	Compétences exigibles	Commentaires
1. Prisme droit, cylindres de révolution	Fabriquer un prisme droit dont la base est un triangle ou un parallélogramme , de dimensions données.	Comme en 6^e , l’objectif est d’entretenir et approfondir les acquis : représenter , décrire et construire des solides de l’espace, en particulier à l’aide de patrons. Passer de l’objet à ses représentations constitue encore l’essentiel du travail, lequel pourra être fait en liaison avec l’enseignement de la technologie.
	Fabriquer un cylindre de révolution dont la base est un cercle de rayon donné
	Représenter à main levée ces deux solides .	L’usage d’outil informatiques ( logiciels de géométrie dans l’espace) peut se révéler utile pour une meilleur visualisation des différentes représentations d’un objet. Ces travaux permettront de consolider les images mentales déjà mises en place , relatives à des situation de parallélisme et d’orthogonalité .
	Calculer le volume d’un prisme droit ,calculer son aire latérale à partir du périmètre de sa base et de sa hauteur .
	Calculer le volume et l’aire latérale d’un cylindre de révolution .	Le parallélépipède rectangle , déjà rencontré en 6^e , est un cas particulier de prisme droit. La formule de son volume est à présent une connaissance exigible.

Contenus	Compétences exigibles	Commentaires
2.Dans le plan, transformation de figures par symétrie centrale : parallélogramme.		Dans un premier temps , l’effort portera sur un travail expérimental ( pliage pour la symétrie axiale et papier calque pour le demi-tour . permettront d’obtenir un inventaire abondant de figures simples . Les propriétés conservées par symétrie centrale seront ainsi progressivement dégagées , en comparant avec la symétrie axiale.
Construction d’images et mise en évidence de conservations .	Construire le symétrique d’un point , d’un segment, d’une droite , d’une demi – droite , d’un cercle.	La symétrie centrale n’a , à aucun moment , à être présenté comme application du plan dans lui – même ; Suivant les cas ? La présence du centre de symétrie ,
Parallélogramme	Connaître et utiliser une définition du parallélogramme et des propriétés relatives aux côtés , aux diagonales et aux angles . Relier les propriétés du parallélogramme à celles de la symétrie centrale .	Le travail entrepris sur le parallélogramme et la symétrie centrale aboutit ainsi à des énoncés que les élèves doivent connaître ; Des situations déductives pourront s’appuyer sur ces énoncés .
	Calculer l’aire d’un parallélogramme.	L’aire du parallélogramme pourra être reliée à celle du rectangle .
Caractéristique angulaire du parallélisme. Liste des fiches (5^ème ) sur les angles : opérations ;adjacents ,complémentaires, supplémentaires, droites parallèles coupées par une sécante ,	Connaître et utiliser les propriétés relatives aux angles formés par deux parallèles et une sécante. Connaître et utiliser les expressions : Angles adjacents Angles complémentaires. Angles supplémentaires .	On pourra utiliser également le vocabulaire : angles opposés par le sommet ; angles alternes externes ;angles alternes internes ; angles correspondants.
Figures simples ayant un centre de symétrie ou des axes de symétries	Reproduire sur papier quadrillé ou pointillé et sur papier blanc , un parallélogramme donné ( et notamment dans des cas particuliers du carré ; du rectangle , du losange ) en utilisant les propriétés.	Les problèmes de construction consolides les connaissances relatives aux quadrilatères usuels et permettront de mettre en œuvre droite et ? de revenir sur la symétrie axiales et les axes de symétrie
	Connaître et utiliser une définition et des propriétés ( relatives aux côtés) , aux diagonales , aux éléments de symétrie ) du carré ; du rectangle ; du losange	On poursuit le travail sur la caractérisation des figures en veillant à toujours la formuler ? d’énoncés séparés .

Contenus	Compétences exigibles	Commentaires
3 TRIANGLE
Somme des angles d’un triangle .	Utiliser dans une situation donnée , la somme des angles d’un triangle . Savoir l’appliquer aux cas particuliers du triangle équilatéral ; d’un triangle rectangle , d’un triangle isocèle	La symétrie centrale ou la caractérisation ? du parallélisme qui en découle permet de démontrer que la somme des angles d’un triangle est égales à 180°. Exemple d’utilisation ? ? ? ?ver quels triangles isocèles ont un angle ? ? degrés.
Construction des triangles et inégalité triangulaire .	Construire un triangle connaissant : La longueur d’un côté et les angles qui lui sont adjacents . Les longueurs de deux côtés et l’angle compris entre ces deux côtés. Les longueurs des trois côtés. Voir cas par cas  les triangles: Scalène ; rectangle ; isocèles ; équilatéraux	On remarquera , dans chaque cas où la construction est possible , que lorsqu’un côté est placé on peut construire plusieurs triangles , deux à deux et symétriques par rapport à ce côté , à sa médiatrice   son milieu. On rencontrera à ce propos l’inégalité triangulaire AB + BC ³ AC dont l’énoncé sera admis . Le ? l’égalité AB +BC = AC sera commenté et illustré ;
Aire d’un triangle	Calculer l’aire d’un triangle connaissant un côté et la hauteur associée .	On pourra relier l’aire du triangle à celle du parallélogramme .
4- Le Cercle : circonscrit à un triangle	Construire un cercle circonscrit à un triangle	La caractérisation de la médiatrice d’un segment à l’aide de l’équidistance a déjà été rencontrée en 6^e . Elle permet de démontrer que les trois médiatrices d’un triangle sont concourantes et justifie la construction du cercle circonscrit à un triangle .
Aire du disque	Calculer l’aire du disque de rayon donné

2°) TRAVAUX NUMERIQUES :

Comme en 6^e , la résolution de problèmes constitue l’objectif fondamental de cette partie du programme . Ces problèmes , en associant à une situation donnée une activité numérique , renforcent le sens des opérations et des écritures numériques et littérales figurant au programme et développent les qualités d’organisation et de gestion de donnés numériques . Il convient donc de ne pas multiplier les activités de technique pure.

L’initiation aux écritures littérales se poursuit , mais le calcul littéral ne figure pas au programme . Les travaux numériques prennent appui sur la pratique du calcul exact ou approché , sous différentes formes souvent complémentaires : le calcul mental , le calcul à la main ( dans le cas de nombres courants et d’opérations techniquement simples ) , l’emploi d’une calculatrice .

Contenus	Compétences exigibles	Commentaires
1. Enchaînement d’opérations sur les nombres entiers et décimaux positifs .
Conventions de priorités entre opérations.	Organiser , pour l’effectuer mentalement , avec papier crayon ou à la calculatrice , une succession d’opérations au vu d’une écriture donnée , de la forme : a+ b c ; a + ;  ;  ; a ( b / c ) ;… uniquement sur des exemple où « a » et « b » et « c » sont uniquement fixés.	L’acquisition des priorités opératoires est le préalable à plusieurs apprentissage :compréhension et mise en pratique de règles . Le fait que les calculatrices n’aient pas toutes les mêmes principes de fonctionnement est une occasion à saisir . En effet , l’activité consistant à répertorier leurs diverses modalités de fonctionnement , et à les mettre en œuvre , est hautement formatrice . On n’oubliera pas de penser , pour éviter d’introduire plusieurs fois un même nombre , à recourir à une mémoire de la machine .

Distributivité de la multiplication par rapport à l’addition.

Connaître et utiliser les identités : k ( a + b ) = ka + kb k ( a - b ) = ka - kb dans les deux sens ( factoriser )

La distributivité est à connaître sous générale d’identité. La comparaison avec une formulation en français –« le produit d’un nombre par la somme de deux nombres est égal à la somme des produits du premier par chacun des deux autres » .. ; pourra être l’occasion de montrer un intérêt ( en économie et précision) de l’écriture symbolique. On entraînera les élèves à la convention usuelle d’écriture « bc » pour « bc » ; « 3a » pour « 3a »  . Les applications donnent lieu à deux types d’activités distinctes : le développement qui correspond au sens de lecture de l’identité indiquée , et la factorisation qui correspond à la lecture "« inverse » : ka + kb = k ( a + b ) . Cette réversibilité se retrouve dans l’initiation à la résolution d’équations.. Cette réversibilité se retrouve dans l’initiation à la résolution d’équations.

Contenus	Compétences exigibles	Commentaires
2. Nombres en écriture fractionnaire.		Toutes les activités numériques fourniront des occasions de pratiquer le calcul mental et d’utilisation de la calculatrice. Plusieurs objectifs sont visés et en particulier développer la capacité à :prévoir des ordres de grandeurs, Opérer en conservant l’écriture fractionnaire. Utiliser le vocabulaire approprié ( terme ; ? ; numérateur ; dénominateur ) Contrôler des résultat par des calculs ? approchés.
Multiplication	Effectuer le produit de deux nombres écrits sous forme fractionnaire ou décimale , le cas d’entiers étant inclus ;
	Exemple 1 :
	Exemple 2 :
	Exemple 3
	Exemple 4 :
	Ramener une division dont le diviseur décimal à une division dont le diviseur est entier .
Comparaison , addition et soustraction , les dénominateurs étant égaux ou multiples	Comparer , additionner et soustraire deux nombres en écriture fractionnaire dans le cas où les dénominateurs sont les mêmes et dans le cas où le dénominateur de l’un est multiple du dénominateur de l’autre ;	La classe de 5^e s’inscrit , pour le calcul avec des écritures fractionnaires , dans un processus prévu dans la durée du collège . En 6^e , le produit et la soustraction de fractions n’ont été envisagés qu’à propos de nombres décimaux . La simplification y a été abordée est doit donc être utilisée en 5^e ; ce sera l’occasion ? ? ? ? des fractions irréductibles mais aucune com ? ? n’est exigible à ce sujet . La systématisation ? ? ? réduction au même dénominateur est traitée en ? ? ?

Contenus	Compétences exigibles	Commentaires
Nombres relatifs en écriture décimale . Les nombres relatifs.	Ranger , soit dans l’ordre croissant , soit dans l’ordre décroissant , des nombres relatifs courants en écriture décimale .	Les activités partirons de l’expérience acquise et pourront s’appuyer sur des interprétations physiques . Elles mettront en place des techniques opératoires concernant l’addition et la soustraction , ? ; ce qui entraînera les élèves à organiser et gérer un organigramme de calcul mettant en jeu des additions et des soustractions avec ou sans calculatrice . A ? ? ?occasion , on observera que soustraire un nombre c’est ajouter son opposé .
WR :expression et somme algébrique	Effectuer la somme de deux nombres relatifs dans les différents cas de signes qui peuvent se présenter . Transformer une soustraction en addition , comme dans l’exemple (LWR : mauvais exemple) - 3,7 – ( -4,3) = -3,7 + 4,3 = 0,6 préférer : (-3,7) – ( -4,3) = (-3,7) + ( + 4,3) = ( + 0,6 )
	Calculer , sur des exemples numériques , une expression où interviennent uniquement les signes + et - et éventuellement des parenthèses.
	Sur des exemples numériques , écrire en utilisant correctement des parenthèses , un programme de calcul portant sur des sommes ou des différences de nombres relatifs.

Contenus	Compétences exigibles	Commentaires
4. Initiation à la résolution d’équations.	Trouver des situations numériques simples , le nombre par lequel diviser un nombre donné pour obtenir un résultat donné.	Le travail sur cette compétence étend au cas ? division l’initiation à la résolution d’équation entreprise en 6^e . Désigner par une lettre le nombre inconnu peut ici se révéler pertinent.
	Tester si une égalité comportant un ou deux nombres indéterminés est vraie lorsqu’ on attribue des valeurs numériques données.	Les programmes prévoient une initiation très progressive à la résolution d’équations , de manière à éviter l’écueil connu d’apprentissage aboutissant à la mise en œuvre d’algorithmes dépourvus de véritable sens . La classe de 5^e correspond à une étape importante dans l’acquisition du sens , avec la présentation d’égalités vues comme des assertions dont la vérité est à examiner . Par exemple , dans l’étude d’une situation conduisant à une égalité telle que 3y = 4x + 2 , on sera amené à tester la véracité pour diverses valeurs de « x » et « y ». Les expressions qui figurent de part et d’autre ? ? ? ? signe d’égalité jouent ici le même rôle . On travaillera aussi avec des inégalités dans des cas simples , sans pour autant que cette activité donne lieu à des compétences exigibles .

3°) ORGANISATION ET GESTION DE DONNEES , FONCTIONS

Les trois parties de cette rubrique s’éclairent et se complètent mutuellement. La contribution des mathématiques à l’éducation du citoyen y apparaît clairement . La partie statistique a pour objectif d’initier à la lecture , à l’interprétation , à la réalisation et à l’utilisation de diagrammes , tableaux et graphiques et d’en faire l’analyse critique . Les outils de description d’une situation sont plus nombreux . Les travaux correspondants ne peuvent se concevoir qu’à partir d’exemples et en liaison , chaque fois qu’il est possible , avec l’enseignement des autres disciplines : sciences de la vie et de la terre , technologie ; géographie ;…

Ils seront l’occasion de consolider et d’approfondir les acquis des élèves sur l’utilisation des unités de mesure , dont celle du temps .

Contenus	Compétences exigibles	Commentaires
1. Activités graphiques
Repérage sur une droite graduée.	Sur une droite graduée : Lire l’abscisse d’un point donné. Placer un point d’abscisse donnée. Déterminer la distance de deux points d’abscisses données.	Les activités graphiques conduiront : A enrichir la correspondance entre nombres et points d’une droite déjà graduée à l’aide de nombres entiers , en développant l’usage des nombres décimaux relatifs. A interpréter l’abscisse d’un point d’une droite graduée en termes de distance et de position par rapport à l’origine , en particulier ,le cas où l’origine est le milieu de deux points donnés mérite de retenir l’attention, A relier la distance de deux points sur un axe et la soustraction des nombres relatifs, A situer les points du plan muni d’un repère orthogonal.
Repérage dans le plan .	Dans le plan muni d’un repère : Lire les coordonnées d’un point donné ; Placer un point de coordonnées données ; Connaître et utiliser le vocabulaire : coordonnées , abscisse , ordonnée

Contenus	Compétences exigibles	Commentaires
2. Exemple de fonctions . Proportionnalité		Toute définition de la notion de fonction sera évitée , mais des expressions telles que « en fonction de » ; »est fonction de «  seront utilisées.
	Reconnaître , s’il y a lieu , la proportionnalité sur un tableau complet de nombres.	On pourra notamment constituer un tableau des abscisses et ordonnées de points passant par l’origine dans le cas muni d’un repère .
	Compléter un tableau de nombres représentant une relation de proportionnalité dont les données sont fournies partiellement . En particulier , déterminer une quatrième proportionnelle .	Les élèves retiendront que dans une relation de proportionnalité , la correspondance est déterminée par un couple de valeur homologues non nulles.
	Mettre en œuvre la proportionnalité dans les cas suivants : Utiliser des unités combinant le système décimal et le système sexagésimal ( mesure de temps). Calculer et utiliser l’échelle d’une carte ou d’un dessin. Reconnaître un mouvement uniforme à la proportionnalité entre « temps » et « distance parcourue » ; utiliser cette proportionnalité . Calculer un pourcentage , un coefficient de proportionnalité . Effectuer pour des volumes des changements d’unités de mesure.	Les activités numériques et graphiques pourront se référer à l’un ou l’autre thème exploitant des formules , notamment de longueur , d’aire et de volume . Ainsi , on pourra envisager des variations : 1. De l’aire d’un triangle ou d’un parallélogramme , de celle d’un disque , 2. De la longueur d’un arc de cercle , de l’aire d’un secteur circulaire, 3. Du volume ou de l’aire latérale d’un cylindre ou d’un prisme droit . En fonction d’une variable de la formule , toute autre variable étant fixée.

Contenus	Compétences exigibles	Commentaires
3.Relevés statistiques.
Lecture , interprétation représentation graphiques de séries statistiques. Classes , effectifs.	Lire et interpréter un tableau , un diagramme à barre , un diagramme circulaire ou semi-circulaire. Regrouper des données statistiques en classes , calculer des effectifs. Présenter une série statistique sous la forme d’un tableau , la représenter sous la forme d’un diagramme ou d’un graphique.	Il importe d’entraîner les élèves à lire et à représenter des données statistiques en utilisant le vocabulaire adéquat. Le calcul d’effectifs cumulés n’est pas une compétence exigible mais il pourra être entrepris , en ? ? ? avec les autres disciplines dans des situations ? ? ? les résultats auront une interprétation. Le choix de la représentation est lié à la nature de la situation étudiée.,
Fréquence	Calculer des fréquences	La notion de fréquence est notamment utilisée pour comparer des populations d’effectifs différents , … ? le lien avec la proportionnalité . les écritures 2/5 ; 0,4 ( ou notation anglo-saxonne 0,4 ?) ; 40% qui peuvent être utilisées pour désigner la fréquence , permettent d’ insister sur les divers représentations d’un même nombre .
VERS la mise à niveau 4e