Pré requis:
|
Notions : droite , segment de droite , point |
|
|
Notion : plan
et demi plan |
ENVIRONNEMENT du
dossier:
|
Index warmaths |
Objectif
précédent 2°) Isométrie |
2°) Symétrie orthogonale
|
1°)tableau |
DOSSIER
Les symétries :
Cours :
L’ISOMETRIE de deux
figures obtenues par pliage et la symétrie axiale
(
symétrie
orthogonale N°1)
|
TEST |
COURS |
|
COURS
Deux segments
sont isométriques s’ ils ont
la même mesure de longueurs .
B) ANGLES ISOMETRIQUES : des
angles sont isométriques si ils ont la même mesure angulaire ( mesure
d’angle)
C ) TRIANGLES ISOMETRIQUES :
Deux triangles sont isométriques s’ ils ont les mêmes mesures
.( longueurs et angles )
D)
En Conclusion : Des figures
géométriques sont dites « isométriques » si elles ont les mêmes
mesures le longueurs et même mesure d’angle .
E) Pliage par
« superposition » un point ; un segment ou une figure est l’obtention d’
une symétrie axiale (elle correspond à une rotation du point ou de la
figure autour d’une droite de 180°
Exemples :
|
Rotation axiale menant à la symétrie axiale |
||
|
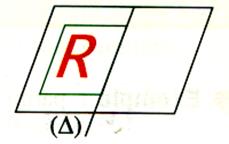
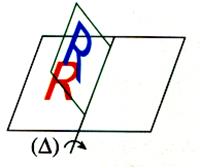
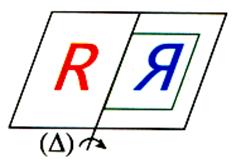
On calque R |
On fait tourner le caque autour de (D) |
On obtient en bleu le symétrique
de R par rapport à la droite (D) |
|
|
|
|
Exemple
d'application
Regardez dans un miroir !!!

Symétrique
axiale d’un point :
|
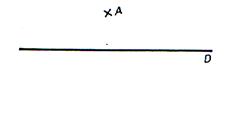
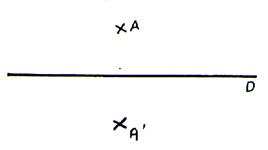
Soit
un point |
Par pliage le point A coïncide avec le point A |
La
symétrie axiale de A est le point A’ |
|
|
|
|
La droite passant par AA’ est perpendiculaire à la
droite « D »
Symétrique
axiale d’un segment:
|
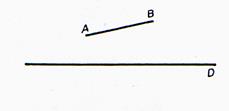
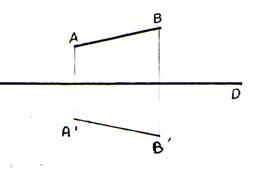
Soit
un segment |
Par pliage le point AB coïncide avec le segment A’B’ |
La
symétrie axiale de AB est le segment A’B’ |
|
|
|
|
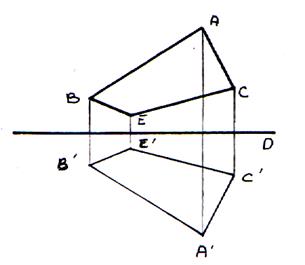
Symétrique
axiale d’un triangle :
|
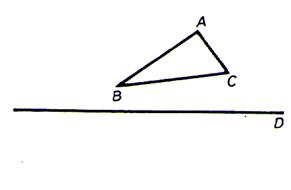
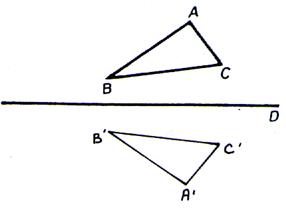
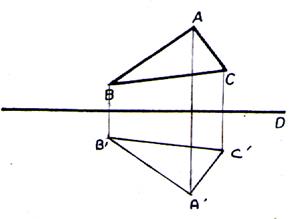
Soit un triangle
(ABC) |
Par pliage le
triangle ABC coïncide avec le triangle
A’B’C’ |
La symétrie
axiale du triangle ABC est le triangle
A’B’C’ |
|
|
|
|
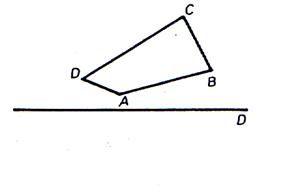
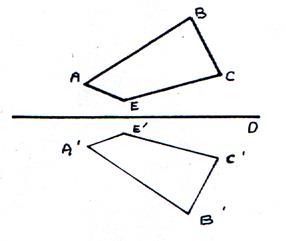
Symétrique
axiale d’un quadrilatère ( ou tout autre figure
plane):
|
Soit
une figure (ABCD) |
Par pliage la figure ABCE
coïncide avec la figure A’B’C’E’ |
La
symétrie axiale de la figure ABCE est la figure A’B’C’E’ |
|
|
|
|
Autres
exemples :
Activités ( 6e ; 5e
) pliages :
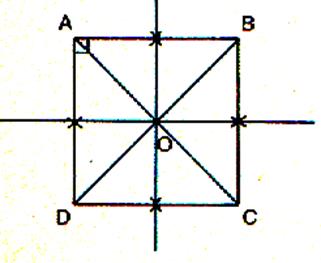
Tracer chaque figure et observer : la figure est découpée par pliage en deux demi- figures
identiques ; la ligne de pliage est appelée : axe de symétrie
|
Le carré : 4 axes de symétrie obtenus par pliage . |
|
|
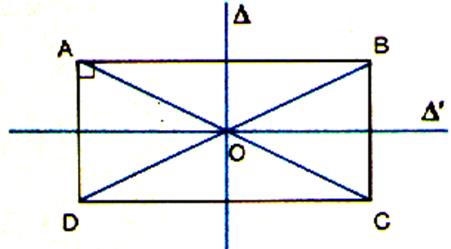
2 axes de symétrie obtenus par
pliage |
|
|
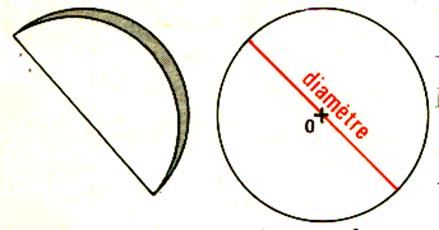
Il possède une infinité d’axes de symétrie. C’est la corde la plus longue ; elle passe par le centre . Elle est appelée « diamètre » |
|
|
|
|
|
|
|
Travaux auto
formatifs.
1°) Deux figures sont
« isométriques » si elles sont ………….
2°) L’isométrie
par rotation est une symétrie ………………
Faire les activités
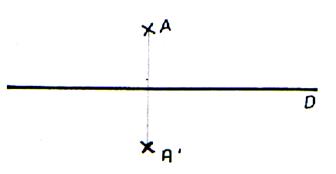
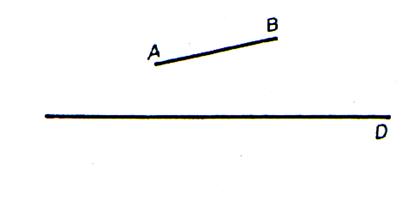
suivantes : Symétrique axiale d’un point :
|
Soit un point |
|
La symétrie axiale de A est le point A’ |
|
|
|
|
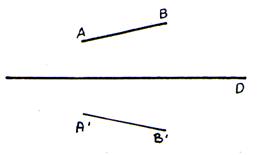
Symétrique axiale d’un segment:
|
Soit un segment |
|
La symétrie axiale de AB est le
segment A’B’ |
|
|
|
|
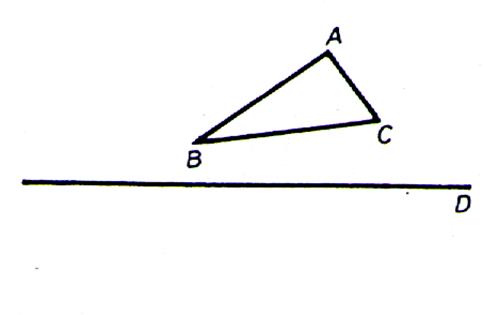
Symétrique axiale d’un triangle :
|
Soit un triangle (ABC) |
La symétrie axiale du triangle ABC est le triangle A’B’C’ |
|
|
|
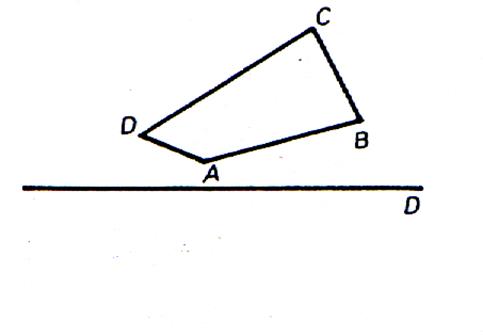
Symétrique axiale d’un quadrilatère ( ou tout autre figure plane):
|
Soit une figure (ABCD) |
La symétrie axiale de la figure ABCE est la
figure A’B’C’E’ |
|
|
|