|
Lecture : Rappels : les figures géométriques sont limitées par des lignes. Ces lignes sont
« droites » (tracées à la règle) ,
soit « courbe » (tracées au compas ) . Mesure de la longueur d’une ligne : « Ligne
droite » :Mesure de la longueur d’une droite : directement
avec une règle graduée ; La mesure de la
longueur d’une droite s’obtient par
calcul : voir « calcul de la mesure d’un segment
sur un axe » ou « calcul de la mesure d’un segment dans un repère. » « ligne courbe » : sa
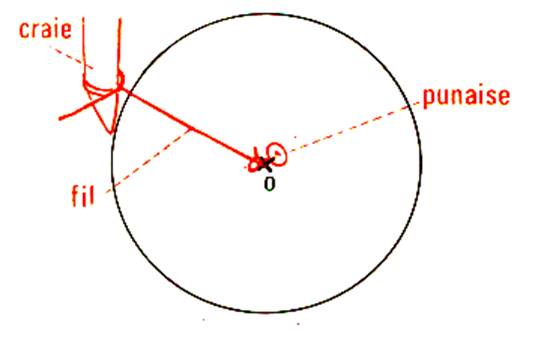
longueur peut s’obtenir par mesure : on pose un fil sur la ligne
courbe ; puis on la tend ce fil ,
on mesure à la règle . Si la courbe est un cercle : faire le calcul de la longueur de la circonférence. Si la courbe est un arc
de cercle : on peut obtenir la longueur par calcul
: il faut connaître le rayon du cercle ,la longueur de l’arc en
degré ,la relation mathématique qui lie le calcul du périmètre du cercle et la partie d’un
angle d’un arc. |
||||
|
Pré requis : |
||||
|
Notions : plan –ligne – point |
Primaire/collège |
|||
|
Info |
||||
|
Le nombre
"pi" |
||||
|
La ligne courbe |
||||
|
ENVIRONNEMENT du
dossier: |
|
|||
|
Index warmaths |
Objectif précédent : Géométrie
présentation |
Objectif
suivant : 1°) Le cercle 2°)Les disques |
tableau |
|
|
|
|
|
|
|
|
DOSSIER « géométrie » cercle et disque » : LE
CERCLE .(notion et terminologie ) |
||||
|
Primaire |
PARTIE 1 : les notions de
base ( tracés , recherche des
caractéristiques et vocabulaire) ; et construction d’un
hexagone. |
|
|
Collège |
PARTIE 2 : CARACTERISTIQUES du
cercle (Termes
employés) |
|
|
|
PARTIE 3 : Récapitulatif des mots désignant
les droites particulières. |
|
|
Un
point O et un nombre R étant donnés , le cercle de
centre O et de rayon R est l’ensemble des points situés dans le plan à la
distance R du point O |
|
|
|||||||||
|
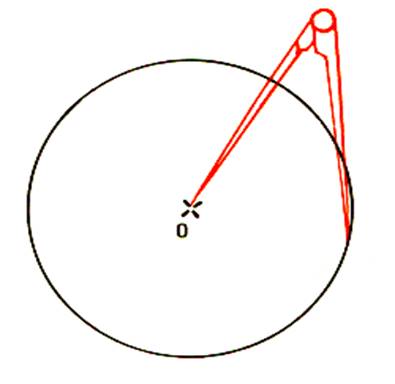
Activité : Marquer
un point O au centre de la page d’une feuille . Prendre
une ouverture de compas égale à 4cm. En
piquant la pointe du compas au point O , tracer un
cercle |
|
||||||||||
|
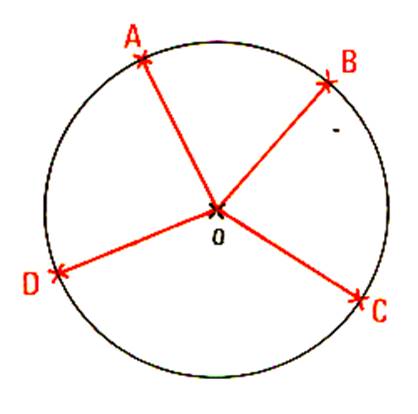
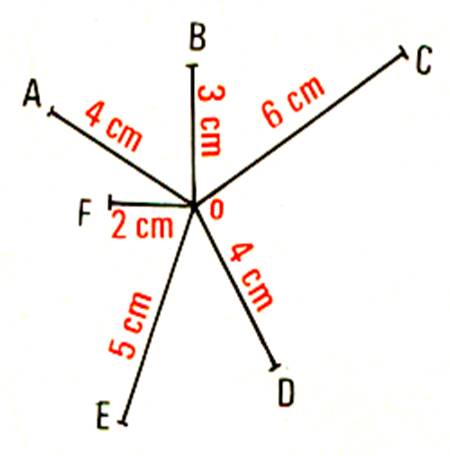
Analyse du tracé : Répondre aux questions suivantes : 1°) Quels sont les segments dont l’extrémité est sur le pourtour du
cercle ( qu’on appelle parfois « circonférence » ? 2°) Quels sont ceux dont l’extrémité est à l’extérieur du
cercle ? 3°) Quels sont ceux dont l’extrémité est à l’intérieur du cercle ? 4°) Sans mesurer , dites à quelle distance de
O les segments OC et OE ont été coupés
. 5°) Quelle longueur manque-t-il au segment OB , au segment OF pour atteindre le
pourtour du cercle ? CONSTRUCTION D’UN HEXAGONE REGULIER. |
|||||||||||
|
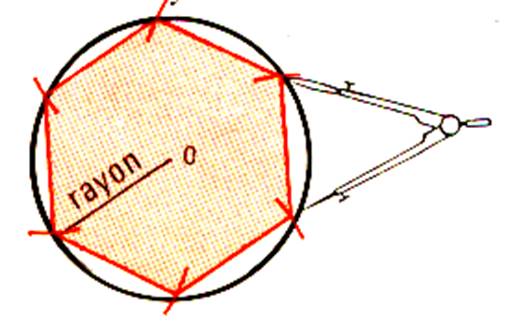
Tracer un cercle de 5cm de rayon . Partageons ce cercle en parties égales
en portant 6 fois le raton. Joignons les points pour obtenir une
figure. La figure colorié est appelée un exagone régulier . |
|
||||||||||
|
|
|||||||||||
|
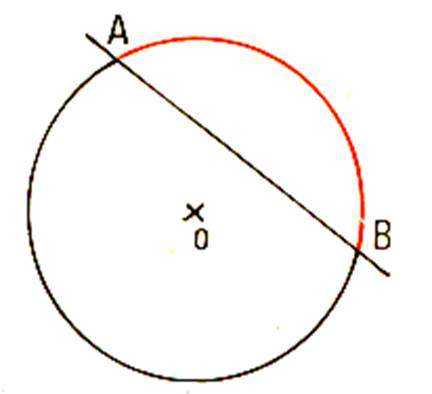
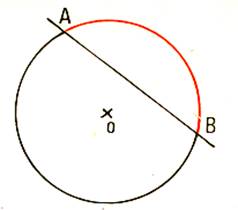
Tracer un cercle : ( de Le segment AB est une « corde » . Chacune des lignes noire et rouge s’appelle un arc de cercle
. |
|
||||||||||
|
Activité 1: |
|||||||||||
|
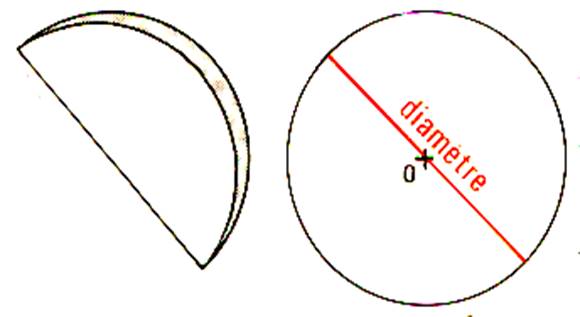
Découper un cercle de 5cm de rayon . Par pliage , déterminons 2 arcs égaux. Marquons le pli en rouge . Cette corde passe par
le centre. C’est le diamètre
. Le mesurer ; quelle longueur
mesure-t-il ; comparer la mesure à celle du rayon. |
|
||||||||||
|
Autre activité 2 : Tracer un cercle et tracer plusieurs diamètres. Nous pouvons
vérifier que ces diamètres sont égaux. Ainsi : 1 diamètre =
2 rayons Autre activité 3 : |
|||||||||||
|
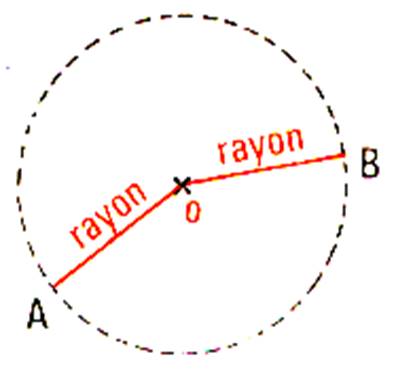
Reproduire le croquis dans lequel : AO + OB
= 2 rayons Pouvons – nous dire que AB est un diamètre du
cercle ? |
|
||||||||||
|
Résumé sur les CARACTERISTIQUES du cercle : Termes employés : |
|||||||||||
|
Est un point intérieur du disque
situé à égal distance de la
circonférence. On dit aussi : Centre : le centre du cercle est le point situé à égale distance de tous les
points qui « cernent » ce point.
On le désigne couramment par la lettre
O. |
|
|
|||||||||
|
Le cercle est une ligne fermée , c’est un ensemble de points . Ces points sont situés dans un
plan à la distance « R » d’un point « O ». Cette ligne est
mesurable (technique : on pose un fil sur le cercle, puis on mesure la longueur du
fil tendu avec une règle). (on parle de mesure du
développé du cercle ) Le cercle est aussi
la frontière du disque . |
|
|
|||||||||
|
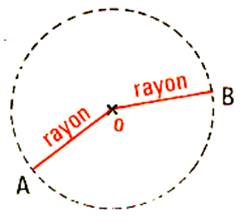
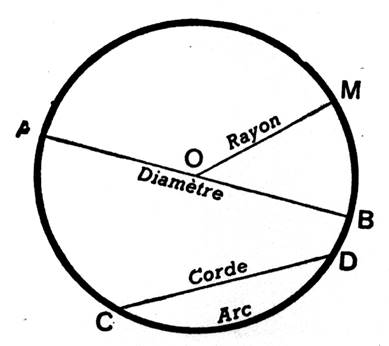
Rayon |
La distance du centre O à un point quelconque du
cercle est le rayon. Le rayon est le segment de droit qui joint le centre à un point quelconque du cercle . Exemple : rayon OC. Tous les rayons d’un même cercle sont égaux. |
|
|
||||||||
|
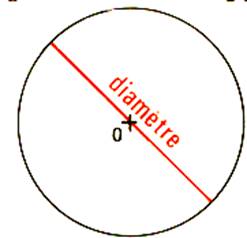
Diamètre |
Le diamètre est une corde qui passe par le
centre , sa mesure est le double de celle d’un rayon . Tous les diamètres
sont isométriques
. ( il partage le cercle ou disque en deux parties égales.) Si « R » désigne la longueur du rayon
et « D » celle du diamètre , nous avons : D = 2R |
|
|
||||||||
|
La longueur du cercle est
appelée « circonférence ». Elle peut se mesurer ,
en général , on calcule la longueur de
la circonférence , avec une formule .
« p »
lire « pi » , c’est un nombre dont la valeur approchée est « 3,14 ». « p »
lire « pi » :
c’est la lettre de l’alphabet grec « p » qui correspond à la première lettre du mot
« periphereia » qui signifie
« contour ». |
Formules : C = 2 fois p fois R Que l’on écrit : C = 2 p R Ou C = p fois
D que l’on écrit : C = p
D |
|
|||||||||
|
Un disque est constitué par l’ensemble des points de la circonférence et de sa région
intérieure. On réserve
le nom de « disque » à la
surface intérieure et de « cercle » à la courbe qui limite le
disque |
|
|
|||||||||
|
AB |
Un arc de circonférence est une portion de circonférence limitée par
deux points. Attention : on calcule la longueur d’ un arc de circonférence .
Cet arc de cercle est engendré par un
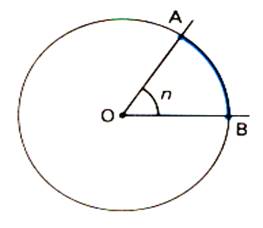
angle « au centre ». Formule : |
|
|
||||||||
|
Une corde est un segment de droite joignant deux points de la
circonférence .Une corde qui passe par le centre est un « diamètre » |
|
|
|||||||||
|
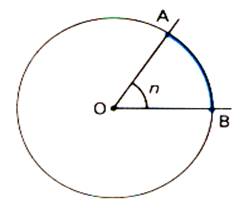
( « n ») |
Un angle au centre est un angle qui a pour sommet le centre du disque
. On dit que l’angle « intercepte l’arc compris entre ses cotés » . « n » est la mesure de l’angle en degré . « AB » est un morceau de la circonférence : |
|
|
||||||||
|
Récapitulatif
sur le nom des droites dans le
cercle : Les droites dans le cercle . |
|||||||||||
|
|
|
||||||||||
|
TRACE d’un cercle : |
|||||||||||
|
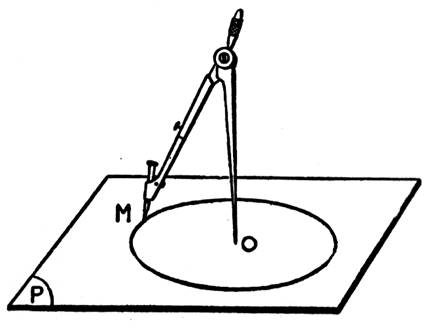
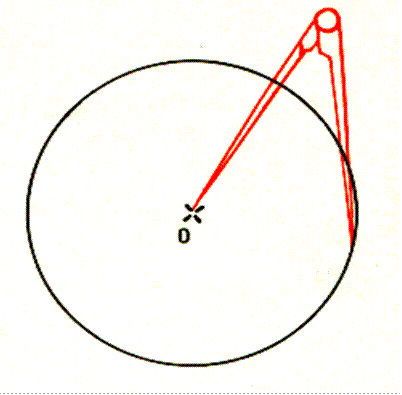
L’outil utilisé pour tracer un cercle est
appelé : COMPAS
|
|
||||||||||
|
Préparation du devoir ; TRAVAUX AUTO - FORMATIFS I ) Donner les définitions des
caractéristiques suivantes |
|||||||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
Rayon |
|
|
|||||||||
|
diamètre |
|
|
|||||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
|
|
||||||||||
|
1°)Tracer
un cercle de tracer et nommer la flèche ; la corde , le
diamètre , le centre, le rayon , une tangente et une sécante 2°) D’un point situé à |
|||||||||||
|
( à
imprimer ) |
|||||||||||