Pré
requis:
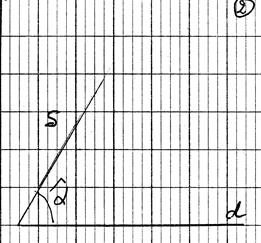
Projection
orthogonale d’un point
|
|
|
BIPOINT |
ENVIRONNEMENT
du dossier:
|
Index |
Objectif précédent |
Objectif suivant |
Tableau |
DOSSIER N° : PROJECTIONS ORTHOGONALES D ' UN SEGMENT.
|
TEST |
COURS |
Devoir Contrôle |
Devoir évaluation |
Interdisciplinarité |
|
Corrigé Contrôle |
Corrigé évaluation |
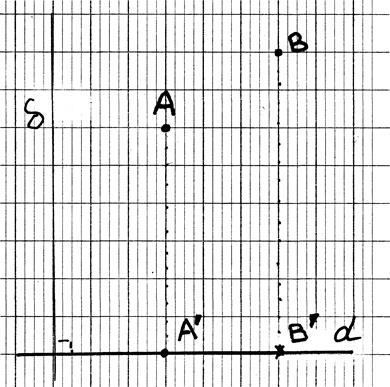
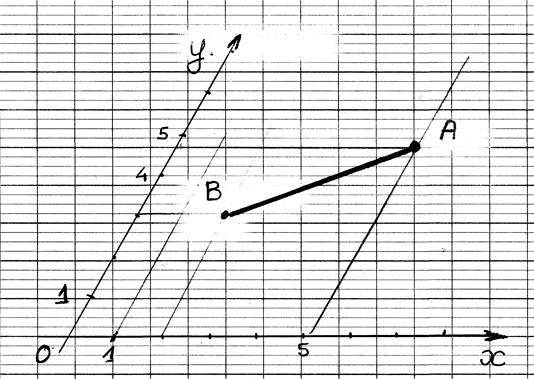
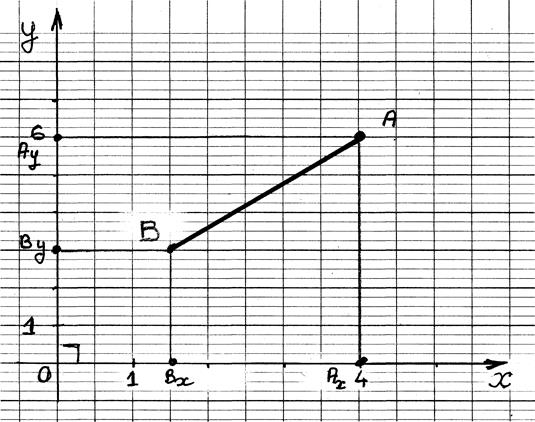
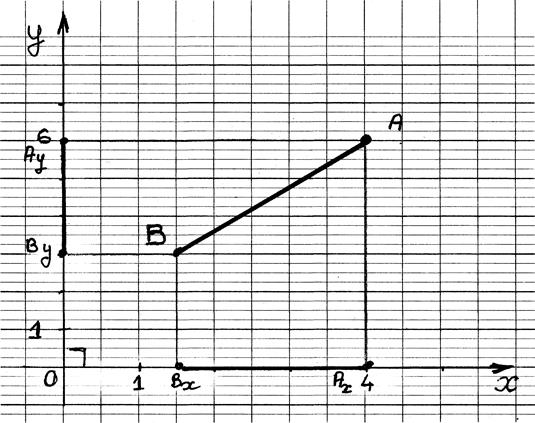
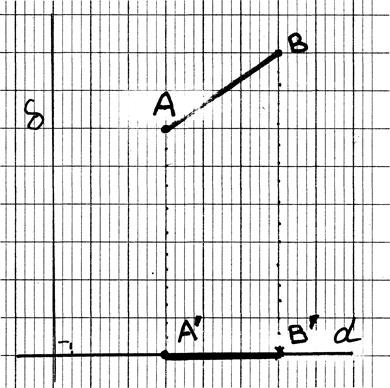
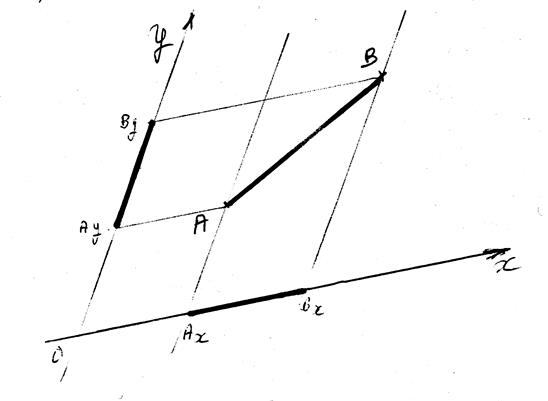
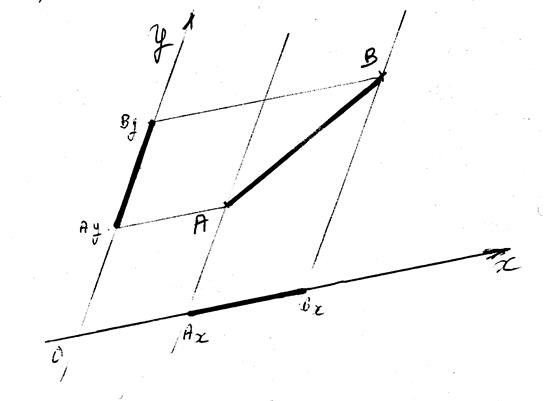
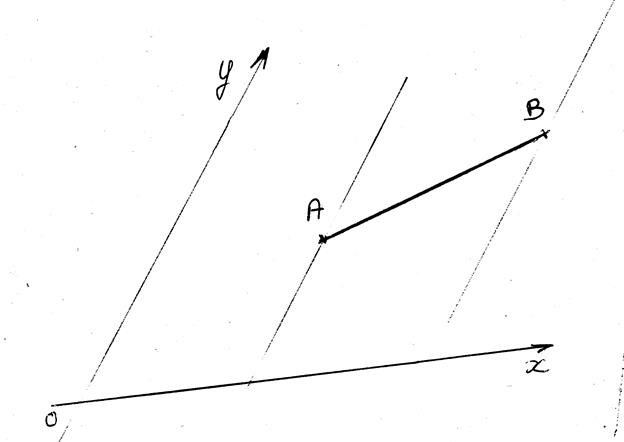
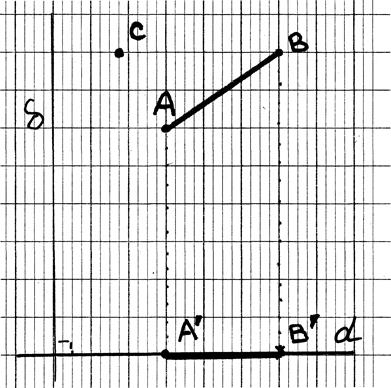
Projections du segment dans un repère orthogonal (Orthonormal)
B
Soit un repère orthonormé ( à compléter):
tracer les projections du segment
AB ; donner les coordonnées des deux points,
B''
échelle1
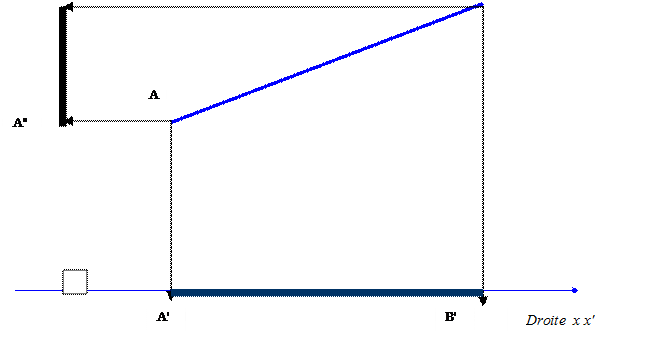
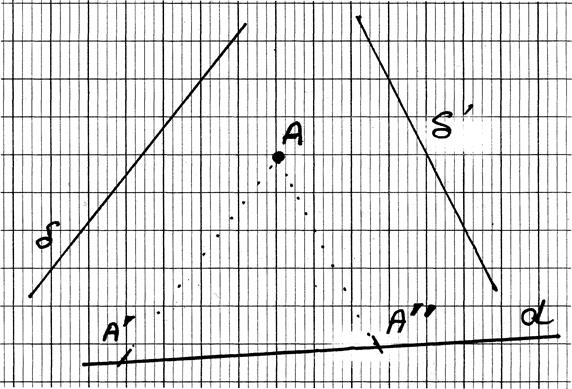
Commentaires:
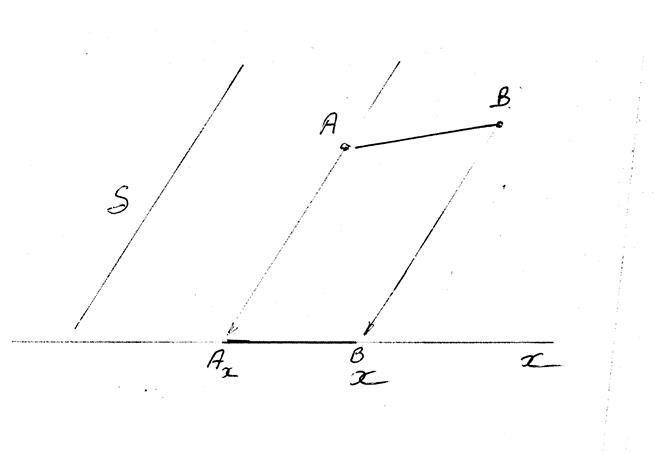
AB
est le segment à projeter:
A'
B' est la projection du segment AB sur l'axe des abscisses.(on dit aussi : le segment A'B' est l'image du segment AB
sur la droite x x' )
A''B"
est la projection du segment AB sur
l'axe des ordonnées. .(on dit aussi : le segment A''B'' est l'image du segment AB sur la droite y
y')
Remarquer que la longueur des segments projetés ne sont pas identiques au segment
projeté.
Ce cas
sera repris avec Obj : « Pythagore » ; et lorsque l'on recherche la norme d’un vecteur par le calcul
|
Pré requis: calcul de la longueur d'un
segment |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
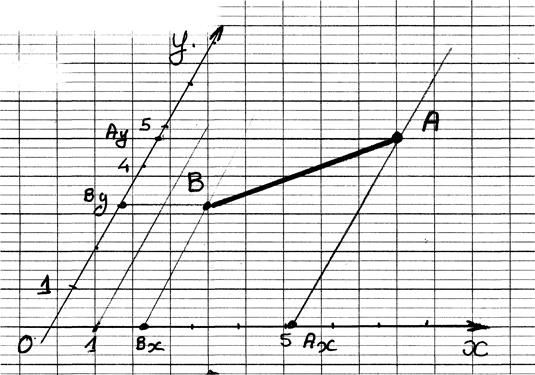
Calcul
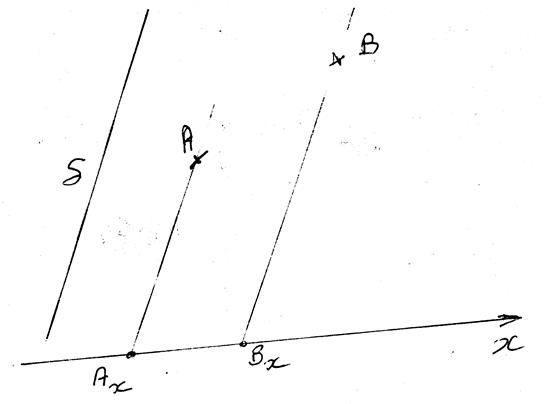
de la longueur du segment A'B' projeté
du segment AB sur xx'
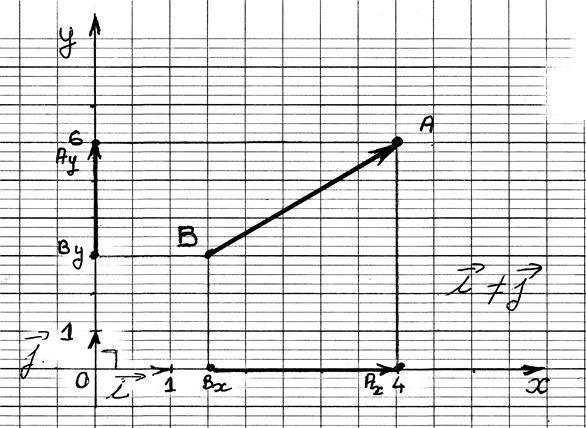
Calcul de la longueur du segment A'B':
le segment A'B':
|
Le point A' à
pour abscisse |
= Ax = ( +3 ) = xA |
|
Le point B' à
pour abscisse |
= Bx = ( + 7 ) = xB |
A savoir :
La longueur d'un segment est égale à la
valeur absolue de la mesure algébrique du bipoint ;représenté
par les bornes du segment multiplié par
le longueur du segment unitaire .
Soit le modèle mathématique
:
|
|
Lg [A'B'] = ½xB - xA
½ Lg
[u] = ½ |
|
Commentaire: couramment on prend
la longueur du segment( unitaire noté
: Lg [u] ); comme valant 1 cm
; cela pour faciliter les calculs et pouvoir vérifier les calculs avec une règle graduée.
Ainsi le modèle mathématique devient :
Lg [A'B'] = ½xB - xA ½ 
1 cm = ½
½ 1cm
Après
simplification : Lg [A'B'] = ½xB - xA ½ = ½½
Applications: Cas où les cordonnées
sont positives
le
segment A'B':
|
A'
à pour abscisse |
=
Ax = ( +3 ) = xA |
|
B'
à pour ordonnée |
= Bx = ( + 7 ) = xB |
|
On
sait que
Lg [A'B'] = ½xB - xA ½ |
calculs |
|
On
remplace xB et
xA par leur valeur donnée |
|
|
Cela
nous donne : Lg [A'B'] = ½(+7) - (+3) ½ |
(+7) - (+3) =
( + (
7 - 3)) = ( +4) |
|
Après
calcul
: Lg [A'B'] = ½(+4)
½ = 4 |
|
|
Conclusion : l'unité de mesure
du segment unitaire étant 1 cm ; la longueur du segment A'B' est de 4 fois 1
cm =
4 cm |
Lg [A'B']
= 4 cm |
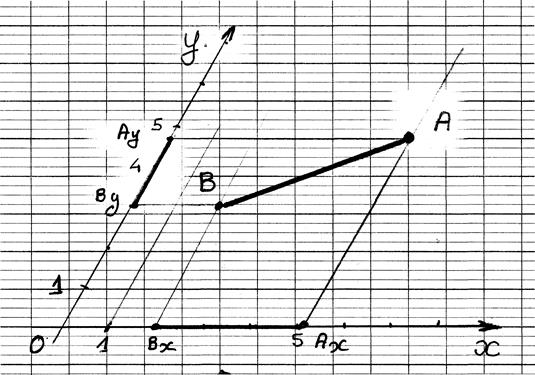
Calcul de la longueur du segment A''B'' projeté du segment AB sur yy'
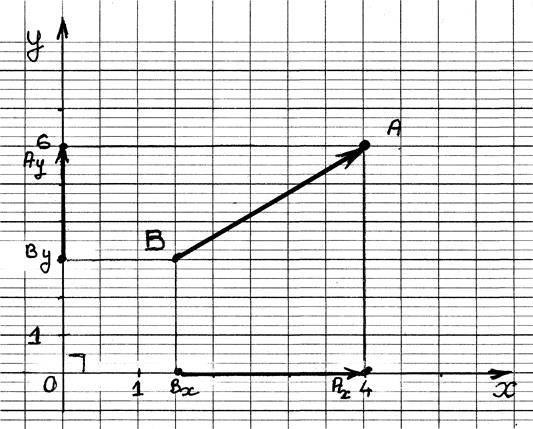
Calcul de la longueur du segment A''B'':
le segment A''B'':
|
A''
à pour ordonnée |
=
Ay = ( +2 ) = yA |
|
B''
à pour ordonnée |
= By = ( + 5 ) = yB |
A savoir :
La longueur d'un segment est égale à la
valeur absolue de la mesure algébrique du bipoint ;représenté
par les bornes du segment multiplié par
le longueur du segment unitaire .
Soit le modèle mathématique
:
|
|
Lg [A''B''] = ½yB'' - yA'' ½ Lg [u]
= ½ |
|
Commentaire: couramment on prend
la longueur du segment( unitaire noté
: Lg [u] ); comme valant 1 cm
; cela pour faciliter les calculs et pouvoir vérifier les calculs avec une règle graduée.
Ainsi le modèle mathématique devient :
Lg [A''B''] = ½yB'' - yA''
½ 
1 cm = ½
½ 1cm
Après
simplification : Lg [A''B''] = ½yB'' - yA'' ½ = ½½
Applications: Cas où les cordonnées
sont positives
le
segment A''B'':
|
A''
à pour ordonnée |
=
Ay = ( +2 ) = yA |
|
B''
à pour ordonnée |
= By = ( + 5 ) = yB |
|
On
sait que Lg
[A''B''] = ½yB'' - yA'' ½ |
calculs |
|
On
remplace yB'' et yA'' par leur
valeur donnée |
|
|
Cela
nous donne : Lg [A''B''] = ½(+5) - (+2) ½ |
(+5) + (- 2) = ;
( +
( 5 - 2)) = ( +3) |
|
Après
calcul
: Lg [A'B'] = ½(+3)
½ = 3 |
|
|
Conclusion : l'unité de mesure
du segment unitaire étant 1 cm ; la longueur du segment A''B'' est de 3 fois
1 cm = 3 cm |
Lg [A''B''] = 3 cm |
CONCLUSIONS:
N°1
|
Le
segment AB (noté [AB] ) à deux composantes dans le repère
cartésien dont on connaît les mesures des longueurs :en utilisant
"Pythagore" il est possible de trouver par le calcul la longueur du
segment AB |
|
(AB) 2= (A'B' )2
+ (A''B'') 2 |
(AB) 2 =
( 4)2 + (3') 2 (AB) 2 =
16 + 9 ( AB) 2 = 25 Donc AB = 5
La
longueur du segment AB est égale à 5 cm |
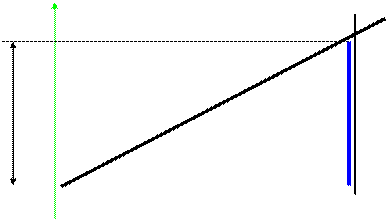
N°2
yA
0
·
xA
A’
A
partir des longueurs des composantes du segment , il est possible de calculer la pente (ce nombre donnera la valeur
numérique de la tangente dont on pourra en déduire la valeur de
l'angle que fait le segment par rapport à l'axe horizontal.
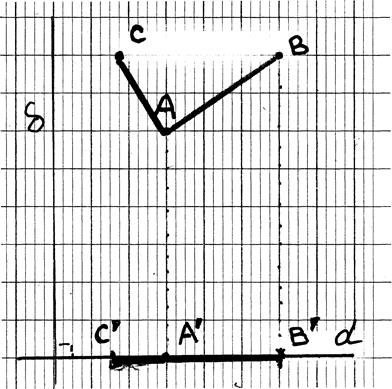
EVALUATION :
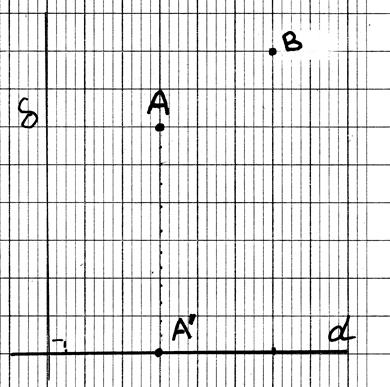
B
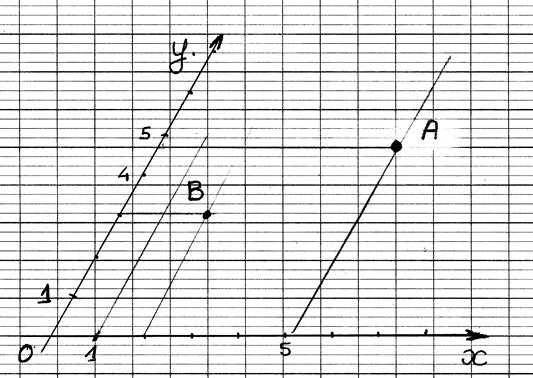
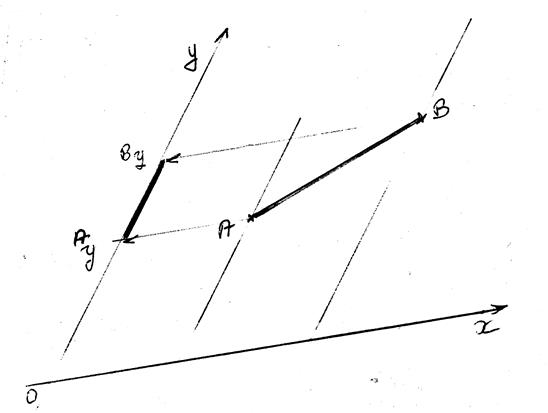
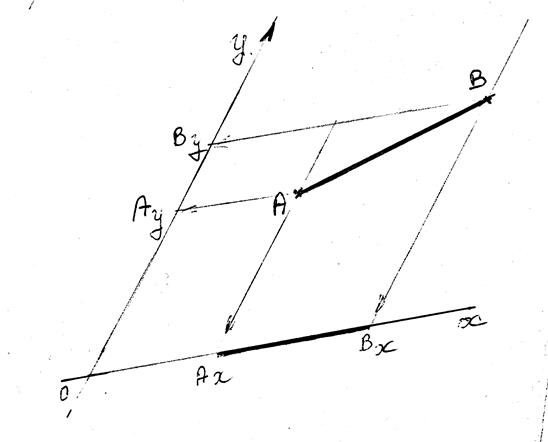
Soit un repère orthonormé ( à
compléter): tracer les projections du
segment AB ; donner les
coordonnées des deux points,
échelle1
