La mesure algébrique ne dépend pas d’un système de mesure de longueur ; c’est un nombre relatif ; la valeur absolue représente le nombre de graduations (la graduation dépend d’ un segment unitaire dont on ignore la longueur.) ; le signe + ou – informe sur le sens de déplacement .

La mesure algébrique est obtenue par calcul ou graphiquement .

Elle est utile en Mécanique ( les vecteurs )

2°) On appelle "longueur" la dimension d'un objet linéaire de l'une à l'autre de ses extrémités.

(l'unité de longueur est le mètre)

3°) On appelle "distance" ,l'intervalle (ou les intervalles )qui existe entre deux points ,ou deux objets.(on dit aussi que c'est le nombre de graduations qui sépare de points sur une droite)

la distance ignore les systèmes de mesure.

Le seul référent est un segment appelé « segment unitaire » qui sert à diviser un morceau de droite , en parties égales . Le nombre de parties égales correspond à la distance rechercher.

( Si l’on veut la longueur de cette droite , il suffit de multiplier la distance par la longueur du segment unitaire )

(L'intervalle est généralement noté "u" associé à un segment de droite d'unité de valeur "1 ")

la « distance » est un nombre décimal qui n ’ a pas d’unité de longueur.

ATTENTION : ne pas confondre "calcul de la longueur d'un segment" et "calcul de la mesure du segment" .

La mesure d’un segment correspond au nombre de graduations qui séparent deux points sur une droite . ( cette mesure peut se faire à partir d’une règle qu’il faut graduer à partir d’un segment unitaire )

La mesurer la longueur d'une segment s’effectue avec une règle graduée , a partir d’un étalon de longueur défini par le système métrique ,

C’est la règle graduer que l’on achète dont la graduation est déterminée par le système métrique ( en cm , mm , …)

Mesurer une distance avec une règle graduée ,c'est déterminer la longueur qui sépare deux points.

La longueur existant entre deux points se mesure avec une règle graduée ou elle se calcule .

Elle se calcule aussi , à condition de connaître le nombre de graduations qui sépare les deux points et la longueur « réelle en cm ,m, ....)d’une graduation.

Définition : La longueur d’un segment est égale à la distance entre deux points ( nombre de graduations) multipliée par la longueur comprise entre les deux points extrêmes d' une graduation « type » dite graduation unitaire.

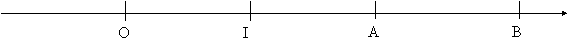
On a pour habitude de donner la définition « restrictive » suivante de la « longueur d ‘ un segment ».

On appelle "longueur d’un segment " la dimension d'un morceau de droite mesurée avec une règle graduée ( la mesure se fait de l’ une à l' autre de ses extrémités).

(l'unité de longueur est le « mètre » ou un de ces multiples ou sous multiples)

I ) LONGUEUR MESUREE directement à la règle graduée .

Cas où la longueur des graduations est égale aux longueurs du système métrique ( multiples ou sous multiples compris)

(lg[OI] = 1cm ) ; lg[OI] = 1dm ; lg[OI] = 1m ; …..)

Exercices types : (voir situation CC )

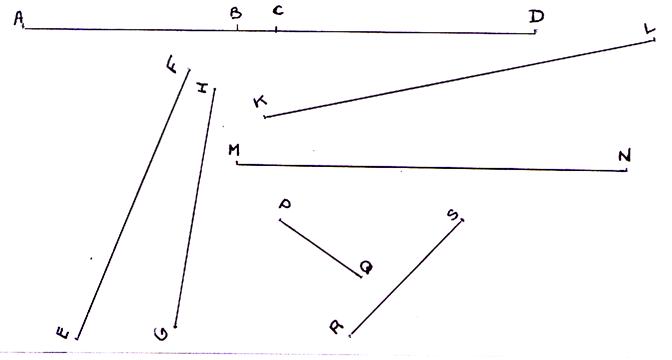
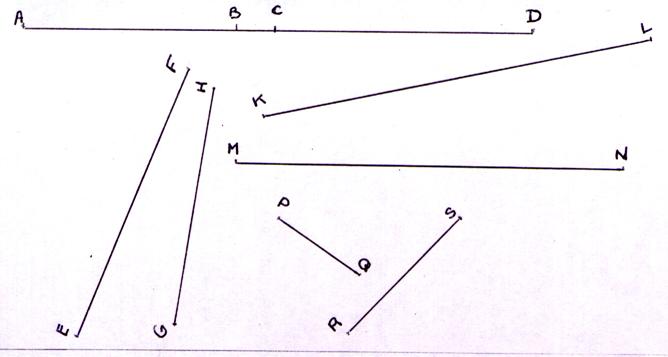
1°) Mesurer la longueur d’un segment :en cm des segments :

[AB ] ; [BC ] ; [CD ] ; [ EF] ; [GH ] ; [KL ] ; [MN ] ; [PQ ] ; [ RS] ;

A ) Mesurer la longueur en cm des segments :

AB ] = ; [BC ] = ; [CD ] = ; [ EF] = ; [GH ] = ;

[KL ] = ; [MN ] = ; [PQ ] = ; [ RS] = ; [ _ _ ] =

B ) Mesurer les segments avec une règle graduée ; donner le résultat au cm prés.

[AB ] = ; [BC ] = ; [CD ] = ; [ EF] = ; [GH ] = ;

[KL ] = ; [MN ] = ; [PQ ] = ; [ RS] = ; [ _ _ ] =

C) Mesurer les segments avec une règle graduée ; donner le résultat au mm prés.

AB ] = ; [BC ] = ; [CD ] = ; [ EF] = ; [GH ] = ;

[KL ] = ; [MN ] = ; [PQ ] = ; [ RS] = ; [ _ _ ] =

D) Mesurer les segments avec une règle graduée ; donner le résultat au ½ mm prés.

AB ] = ; [BC ] = ; [CD ] = ; [ EF] = ; [GH ] = ;

[KL ] = ; [MN ] = ; [PQ ] = ; [ RS] = ; [ _ _ ] =

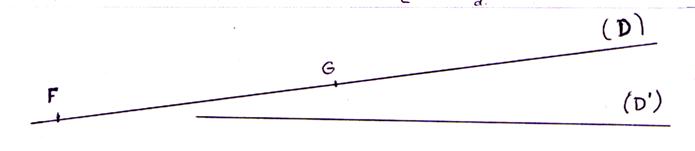
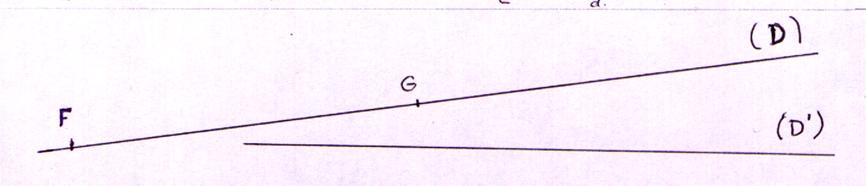
2°)Tracé d’un segment :

a) Tracer sur la droite ( D ) un segment AB de longueur 137 mm

b)Tracer sur la droite (D’) un segment [ F’ G’ ] isométrique au segment FG

II ) LONGUEUR MESUREE directement à la règle graduée .

Cas où la longueur des graduations n ‘ont une longueur égale aux longueurs du système métrique ( multiples ou sous multiples compris)

Exemple lg[OI] = 1,5 cm

Soit une droite graduée , un point « O » d ‘ abscisse « 0 » , un point « I » d ‘abscisse « 1 » , un point « A » d ‘abscisse « x_A » et un point « B » d ‘« abscisse « x_B »

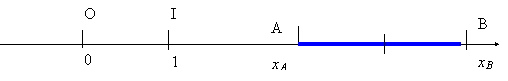
*Le bipoint (O,I) est appelé « bipoint unité » d’unité « 1 » ,

Le segment de droite ayant pour bornes incluses une longueur de 1,5 cm

Notation du segment unitaire	[OI ]
Notation de la longueur du segment unitaire	Lg [OI] = 1,5 cm

La Longueur du segment AB: noté " Lg [AB] "

Exemple :

La longueur du segment AB est égale à 2 fois la longueurs du segment OI: 2 fois 1,5 cm = 3 cm

Calcul de la longueur du segment AB:

La longueur d'un segment est égale à la valeur absolue de la mesure algébrique du bipoint ;représenté par les bornes du segment multiplié par le longueur du segment unitaire .

Soit le modèle mathématique :

Lg [AB] = ½x_B- x_A ½ Lg [u] = ½½ Lg [u]

TRAVAUX AUTO FORMATIFS.

CONTROLE

1°)Qu'appelle t on "mesure"

2°) Qu'appelle t on "longueur "

3°) Qu'appelle t on "distance"

4°) Quelles sont les méthodes qui permettent d’obtenir la longueur d’un segment .

(précisez)

EVALUATION

1°) Mesurer la longueur d’un segment :en cm des segments :

[AB ] ; [BC ] ; [CD ] ; [ EF] ; [GH ] ; [KL ] ; [MN ] ; [PQ ] ; [ RS] ;

A ) Mesurer la longueur en cm des segments :

AB ] = ; [BC ] = ; [CD ] = ; [ EF] = ; [GH ] = ;

[KL ] = ; [MN ] = ; [PQ ] = ; [ RS] = ; [ _ _ ] =

B ) Mesurer les segments avec une règle graduée ; donner le résultat au cm prés.

[AB ] = ; [BC ] = ; [CD ] = ; [ EF] = ; [GH ] = ;

[KL ] = ; [MN ] = ; [PQ ] = ; [ RS] = ; [ _ _ ] =

C) Mesurer les segments avec une règle graduée ; donner le résultat au mm prés.

AB ] = ; [BC ] = ; [CD ] = ; [ EF] = ; [GH ] = ;

[KL ] = ; [MN ] = ; [PQ ] = ; [ RS] = ; [ _ _ ] =

D) Mesurer les segments avec une règle graduée ; donner le résultat au ½ mm prés.

AB ] = ; [BC ] = ; [CD ] = ; [ EF] = ; [GH ] = ;

[KL ] = ; [MN ] = ; [PQ ] = ; [ RS] = ; [ _ _ ] =

2°)Tracé d’un segment :

a) Tracer sur la droite ( D ) un segment AB de longueur 137 mm

b)Tracer sur la droite (D’) un segment [ F’ G’ ] isométrique au segment FG

Problèmes

N° 1:

Enoncé : lg[OI] = 1,5 cm

calculer êê=

avec A (+3) et B (+5)

Donner les deux solutions :graphiques et par le calcul.

N°2

Enoncé : lg[OI] = 1,5 cm

calculer êê= ( lire : la distance entre deux points est égale à la mesure algébrique...)avec A (+3) et B (-5)

Donner les deux solutions :graphiques et par le calcul.

INTERDISCIPLINARITE

1°) Géographie : Les longueurs des grands fleuves français .

Ces 4 segments de droites figurent les 4 grands fleuves français.

Légende : chaque cm représente 100 km.

Questions :

Mesurer la longueur de chaque segment.

Calculer la longueur de chaque fleuve .

	Loire	Rhône	Seine	Garonne
Lg en cm
Lg en km

1°) Sciences naturelles : la vitesse des animaux

Informations : voici les vitesses de certains animaux

En prenant 1 mm pour représenter 1 km , tracer des segments qui symboliseront la distance parcourue par chaque animal s’il conservait cette vitesse pendant une heure .