|
|
|
|
|
|
ENVIRONNEMENT
du dossier:
|
Objectif
précédent |
|||||
|
|
|||||
|
|
LES
PRISMES DROITS . |
|
|||
|
|
|
|
|||
|
|
I)
Exemples et définition. |
|
|||
|
|
II) Calcul du volume du prisme droit . |
|
|||
|
TEST |
COURS |
Interdisciplinarité
|
|
Corrigé
Contrôle |
Corrigé
évaluation |
||
|
|
Travaux niv VI et
V: Dos 191 |
|
|
||||
|
|
|
|
|
|
Définition :
Un prisme est « droit » si les arêtes latérales ont des supports
perpendiculaires aux plans de base. |
|
|
|
·
Les surfaces latérales sont des
rectangles.
· Le
prisme est posé sur une base. |
|
|
|
|
|
|
|
Un
parallélépipède droit est un prisme dont les bases sont
des parallélogrammes |
|
|
|
|
|
|
|
|
|
|
|
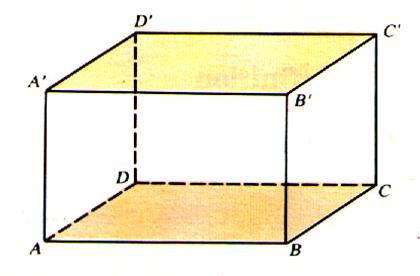
Le parallélépipède
rectangle :
Un parallélépipède rectangle est un prisme droit dont les bases sont des rectangles . |
|
|
|
|
|
|
|
Remarque : Le cube est un
prisme droit |
|
|
|
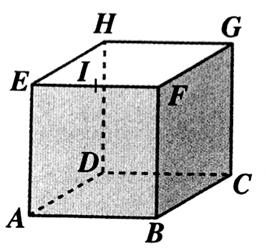
Cas
particulier : le cube |
|
|
|
Ci dessous : Le cube
|
|
|
|
Remarque :
Le parallélépipède rectangle est un prisme droit
|
|
|
|
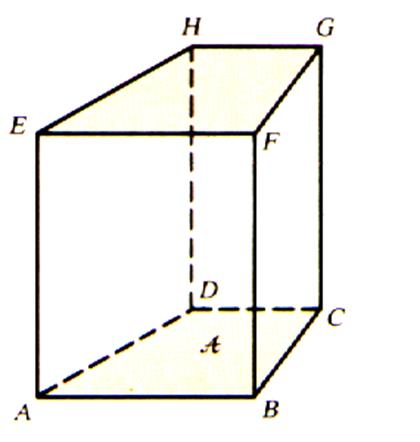
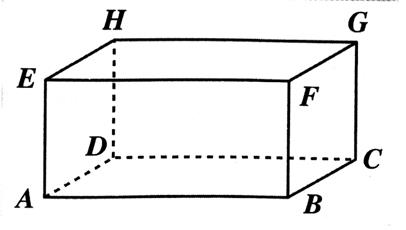
Ci dessus et ci - dessous : Le parallélépipède rectangle (dit aussi : pavé)
|
|
|
|
|
|
|
|
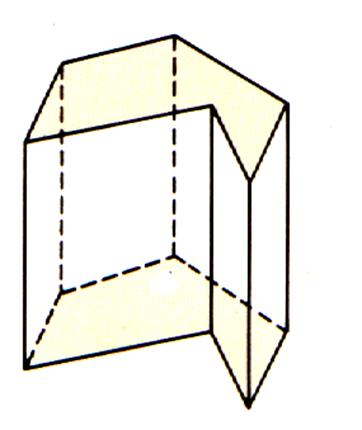
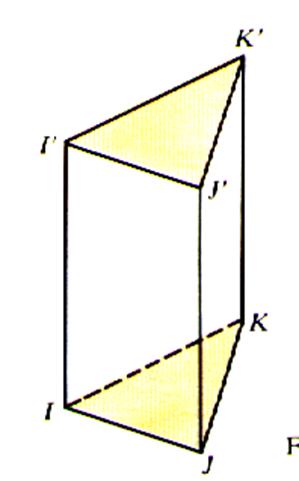
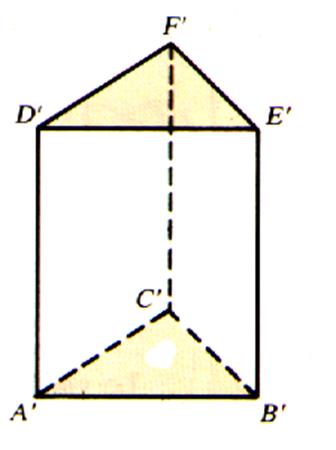
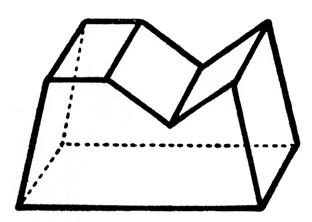
Autres exemples : à base triangulaire .
|
|
|
|
à base triangulaire |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
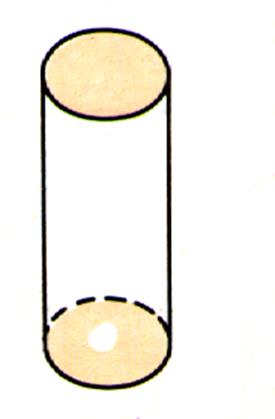
Cylindre
droit : ( qui est aussi un solide de révolution)
|
|
|
|
|
|
|
|
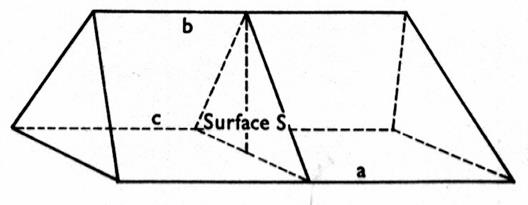
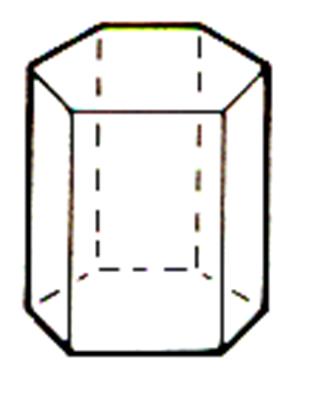
Prisme
droit à section hexagonale
|
|
|
|
( à vous d’en imaginer un autre
) ( voir « les
polygones »)
|
|
|
|
INFO plus ++++ |
|
|
|
Parallélépipèdes rectangles |
|
|
|
Cubes |
|
|
|
cylindres |
|
|
|
II) Calcul du volume du prisme droit : |
|
|
|
Si
l’on veut connaître le volume (V) de ces prismes il suffit de multiplier la
surface de base ( Sb) par la hauteur (h) du prisme. Ce qui permet d’écrire la formule (mathématique
) suivante : V
= Sb . h (nota : Une formule est appelée aussi
« expression algébrique » ;
le point qui sépare dans la formule
« Sb » et
« h » représente
le signe « multiplier » ) Exemple 1 : Un bassin de 3 m² est alimenté par un
robinet. Le niveau de l’eau monte
alors de 90 cm. Quel est le volume du bassin
? Réponse :
volume du bassin : 3 fois 0,9 = 2, 7 m3 |
|
|
|
|
|
