Module : .		DOSSIER : 156 - 157
warmaths ; Pour Aide et Formation Individualisée ; REMEDIATION mise à /NIVEAU : niveau VI
Info conseils et consignes.	TRAVAUX NORMATIFS PRIMAIRE / COLLEGE : / Reprise lycée. Matière : MATHEMATIQUES. Niveau VI - V - IV			.>>>>EXO cours (à donner à faire aux élèves)
VOLUME DU PARALLELEPIPEDE rectangle (dit aussi « pavé ») et du CUBE.
INFO COURS :
Info 1 @ « cours sur dos. 152 - 153… » ; Info 2 @ « cours sur 146 - 147… » ; Info 3 @ « cours niveau V »
TRAVAUX CONTROLE
Doc WR
Les questions relatives à « ce qu’il faut retenir » , au « savoir » se reporter aux cours .
TRAVAUX : EVALUATION
Le volume d’un corps s’évalue en le comparant aux cubes - unités de volume. Or, ces cubes n’existent pas en réalité on a recours, non. à des mesures, mais à des calculs, selon des formules ingénieusement établies (à apprendre).
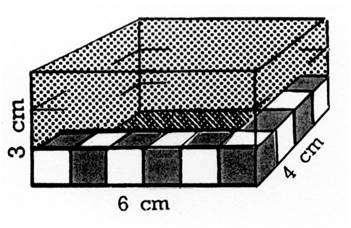
			Le parallélépipède rectangle représenté ci-contre mesure 6 cm de long, 4 cm de large, 3 cm de hauteur. On pourrait « théoriquement » placer sur sa base 4 bandes de 6 fois 1 cm^3soit l’ opération « 6 x 4 » = 24 cm^3 et, en hauteur 3 couches de 24 cm^3soit l’opération « 24 x 3 » =72cm^3 Le volume est donc connu par le calcul : 6 x 4 x 3 = 72
Soit mesure de la longueur x mesure de la largeur ´ mesure de la hauteur ou surface de base x mesure de la hauteur
Il faut prendre ces mesures avec la même unité de longueur, et on obtient le produit (volume) dans l’unité de volume correspondante. Formules. Volume du parallélépipède rectangle V = L x l x h ou V = S de base x h Le cube est un parallélépipède rectangle aux 3 dimensions égales; formules pour le cube: V = arête x arête x arête ; Ou V = S d’une face x arête.

1. Copiez et complétez le tableau suivant, concernant des parallélépipèdes rectangles:
longueur	12 cm		0,9 m		8 cm		8 m		12 m
largeur	8 cm		0,75 m		45 mm		7,5 m		2,5 m
hauteur	10 cm		60 cm		32 mm		3,5 m		5 cm
surface de base	………….		………….		………….		………….		………….
volume	………….		………….		………….		………….		………….
2. Copiez et complétez le tableau suivant, concernant des cubes
Arête		4 cm		10 cm		1,2 m		0,25 m		0,40 m
Surface d’une face
Surface totale
volume
3. Une citerne cubique mesure 1,5 m d’arête. Indiquez le calcul de son volume : a) en m^3 b) en dm^3. Quelle règle des mesures de volume retrouvez-vous dans les résultats? 4. Une boîte parallélépipédique mesure 24 cm de long, 18 cm de large, 16 cm de haut. a) Évaluez ses dimensions en dm, puis en m. b) Calculez son volume : en cm^3, en dm^3, en m^3. c) Citez la règle des mesures de volume que vous vérifiez ainsi. 5. On creuse une fosse de 2,4 m de long, 1,8 m de large, 1,5 m de profondeur. Le terrassier qui la creuse reçoit 24 € par m^3enlevé. Combien reçoit-il ? 6. A 47,50 € la tonne, combien coûte un bloc de pierre cubique de 0,8 m d’arête, le décimètre cube de pierre pesant 2,6 kg? 7. Combien le volume d’un cube de 16 cm d’arête vaut-il de fois le volume d’un cube de 8 cm d’arête ? Donnez la réponse a) par le calcul; b) par le raisonnement, en vous aidant d’un croquis . 8. Un pilier est formé de cinq pierres cubiques superposées ayant chacune 0,65 ni d’arête. Calculez : a) la hauteur du pilier; b) son volume en mètres cubes; c) sa masse le décimètre cube de pierre pesant 2,600 kg. 9. Dites le volume d’un livre de 20 cm de long, 10 cm de large, 3 cm d’épaisseur; d’une chambre de 5 m sur 4 ni, et 3 m de haut; d’une valise de 1 ni sur 0,6 ni, et 0,25 ni d’épaisseur; d’une boîte de 20 cm sur 16 cm, et 10 cm de profondeur; d’un mur épais de 0,5 ni, long de 16 m et haut de 3 m. 10. Une salle de classe mesure 7 ni de long, 6,5 m de large et 4 m de haut. Combien d’élèves peuvent y séjourner avec leur maître, chaque personne devant disposer de 5 m ^3d’air ? 11. Un terrassier creuse une fosse cubique de 1,5 m d’arête. La terre remuée augmente de un cinquième de son volume primitif, a) Quel volume a-t-elle après son extraction? b) Pour emporter la terre enlevée, le terrassier utilise une brouette contenant 45 dm^3. 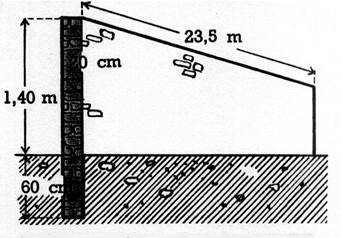Combien emplira-t-il de fois sa brouette? 12. Un mur, enfoncé de 60 cm dans le sol, s’élève de 1,40 ni au-dessus du sol. Sa longueur est 23,5 m, son épaisseur 20 cm. a) Quel est le volume de la maçonnerie ? b) Le mur a coûté 1546,30 € . Quelle question pouvez-vous poser ? Posez-la, répondez-y.
13. La caisse d’un camion mesure 3,5 m de long, 2 m de large, 80 cm de hauteur. Elle contient une hauteur de 60 cm de sable qui pèse 2,7 t par mètre cube, a) Quel est le volume de la caisse ? b) Quel est le volume du sable transporté? c) Quel est le poids de ce sable ? d) Vous n’avez pas utilisé le nombre qui mesure le volume de la caisse quelle question pouvez-vous poser ? Faites-le, répondez-y. 14. Un tas de fumier parallélépipédique mesure 6 m de long, 4 m de large et 1,6 m de haut. Le cultivateur le transporte dans un chariot de 2,4 m^3 et le répand sur un champ à raison de 0,5 m ^3 pour 2 ares de terrain, a) Combien fait-il de voyages aller et retour ? b) Quelle surface peut-il couvrir ?
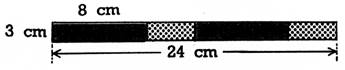
15 . Le dessin ci-contre est le début du développement d’un parallélépipède rectangle; reproduisez-le et achevez-le. Dites quelles sont les dimensions de ce parallélépipède, et quel est son volume, une fois construit.
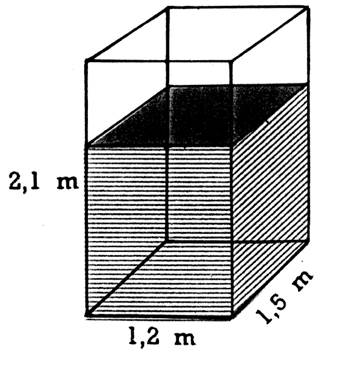
16. La citerne d’eau d’une ferme du Jura a les dimensions indiquées sur la figure ci-contre. a) Quel est son volume ? b) Elle est pleine aux deux tiers. Quelle hauteur d’eau contient-elle alors ? c) Calculez de 2 façons le volume d’eau qu’elle contient. d) On y puise 250 dm^3 d’eau par jour. Y restera-t-il de l’eau au bout de 10 jours ?