|
|
|
|
|
ENVIRONNEMENT du dossier:
|
1°)
le parallélépipède rectangle |
1°)
Le cube comme unité et instruments de mesure des volumes. |
3. liste des
cours sur : unités-conversions-périmètre-aire-volume ……. |
|||
|
|
|||||
|
|
CUBE ( ou un pavé) :
Définition et le développement
du cube |
|
|||
|
|
-
Exemples de
cubes et de a représentation en perspective
. |
|
|||
|
|
-
Le cube : (définition) |
|
|||
|
|
-
Développement du cube |
|
|||
|
|
-
Aire latérale |
|
|||
DOSSIER :
-
|
TEST |
COURS |
|
|
|
|
|
|
|
|
|
|
|
Exemples de cubes et ses représentations en perspective : |
|
|
|
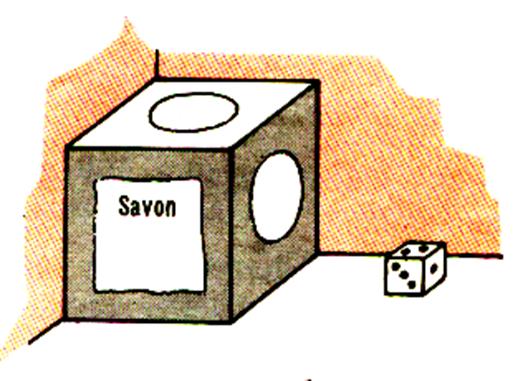
1°) Le "Dé" à jouer :
|
|
|
|
Le cube en perspective :
|
|
|
|
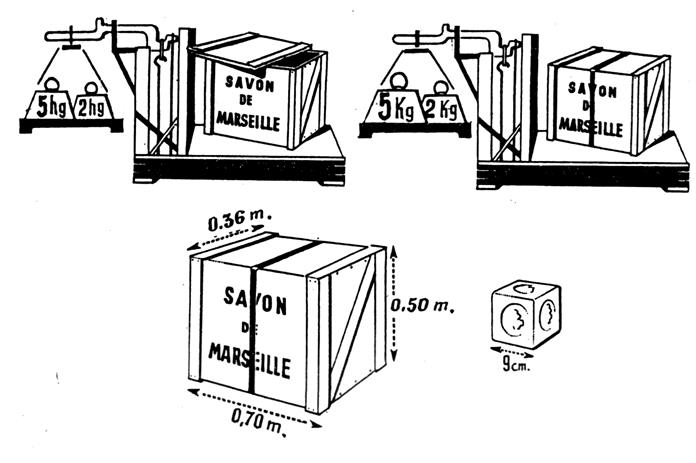
2°) un morceau de savon de Marseille,.. |
|
|
|
|
|
|
|
|
|
|
|
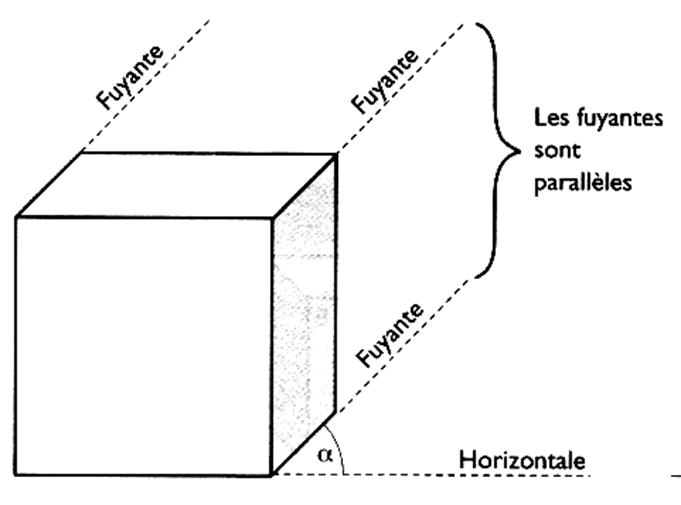
Info sur
la représentation du cube en
perspective : (info plus sur les
perspectives) |
|
|
|
|
|
|
|
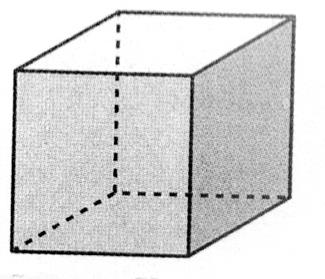
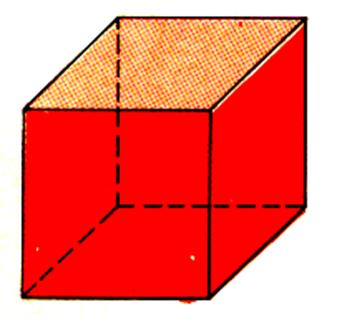
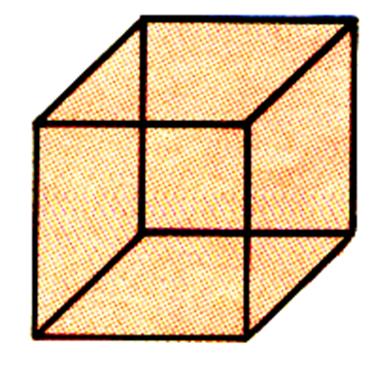
Un cube vu en « non transparent » :
|
|
|
|
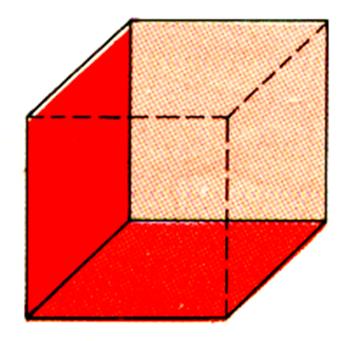
Un cube vu en transparence : |
|
|
|
|
|
|
|
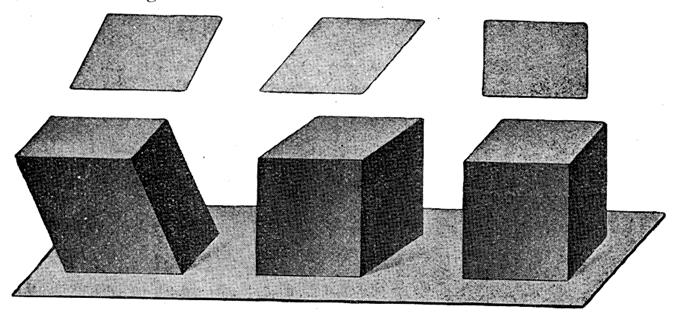
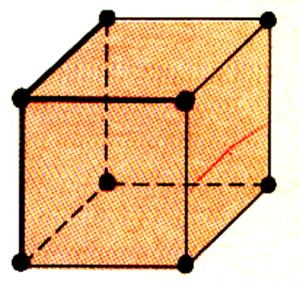
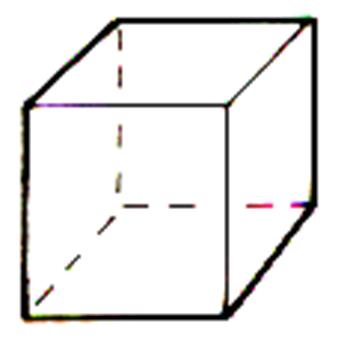
Ci
dessous 3 solides , seul celui du milieu représente
un cube. |
|
|
|
|
|
|
|
Celui de gauche n’est pas un cube :
|
|
|
|
Celui du milieu est un cube : |
|
|
|
|
|
|
|
Celui de droite est appelé : un pavé .
( voir le parallélépipède rectangle ) |
|
|
|
|
|
|
|
|
|
|
|
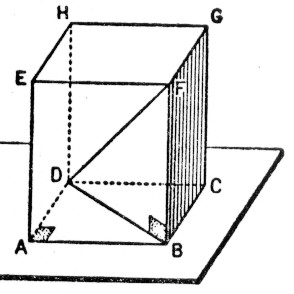
Représentation
d’un cube en perspective |
|
|
|
|
|
|
|
|
|
|
|
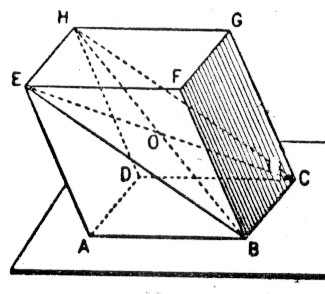
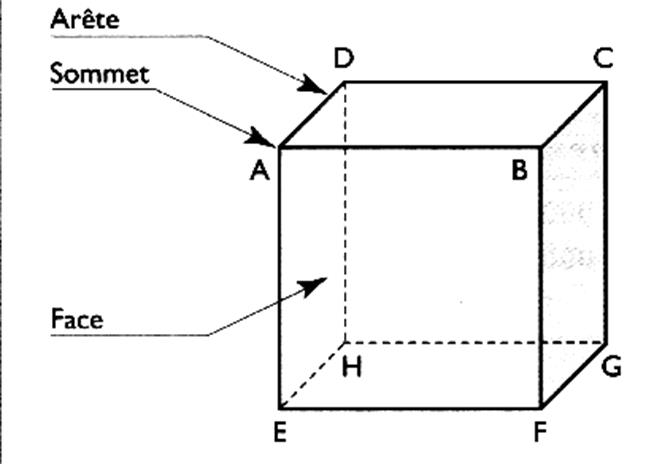
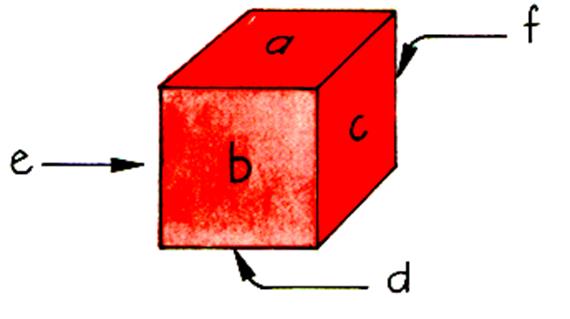
Tel qu’il est
dessiné le cube est posé sur sa base
DHGC ; son autre base est AEFB Les
faces latérales : sont ABDC
(vue de face ) Les
vues de coté sont celle : De
gauche : EADH De
droite BFGC Et
d’arrière : EFGH ou ( FEHG) |
|
|
|
|
|
|
|
|
|
|
|
Le cube : (définition) |
|
|
|
a) Il a 6 faces carrées :Les faces opposées
sont parallèles deux à deux et les faces ayant une arête commune sont
perpendiculaires . Chaque face étant un carré , les arêtes opposées d'une face sont parallèles . |
|
|
|
|
|
|
|
Les arêtes : |
|
|
|
Il
possède 12 arêtes de même longueur . Les
arêtes aboutissant à un même sommet
sont perpendiculaires deux à deux . |
|
|
|
|
|
|
|
Les sommets : |
|
|
|
Il
a 8 sommets. ; * 3 arêtes aboutissent
à chaque sommet . |
|
|
|
|
|
|
|
Le
cube est un parallélépipède dont les six faces
sont des carrés égaux . |
|
|
|
Le cube a six faces égales et douze arêtes. Deux des carrés forment les bases et les quatre
autres les côtés. |
|
|
|
|
|
|
|
Activités: |
|
|
|
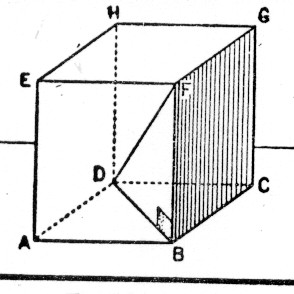
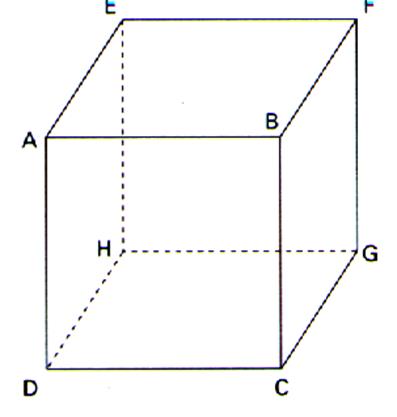
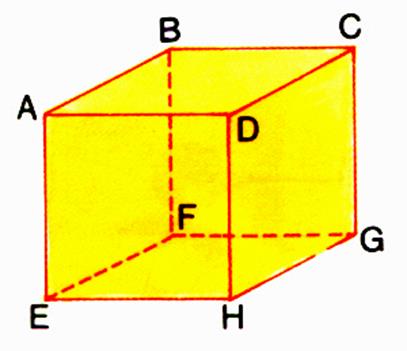
En vous aidant de la figure suivante : |
|
|
|
citer : -
deux arêtes parallèles :…………………………………. -
deux arêtes perpendiculaires :…………………………… -
deux faces parallèles : …………………………………… - deux faces
perpendiculaires : …………………………….. |
|
|
|
|
|
|
|
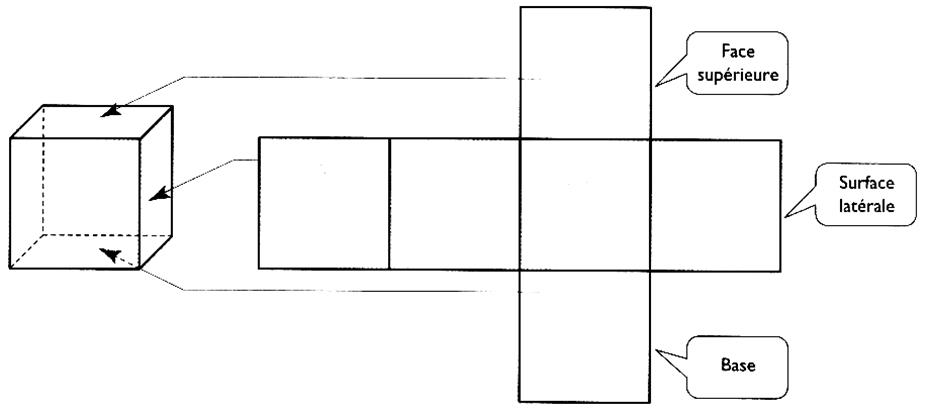
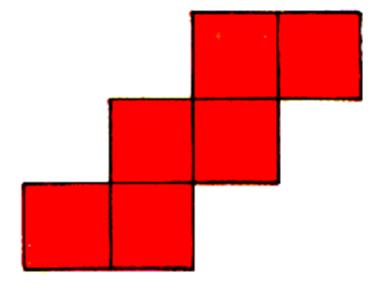
Développement du cube : |
|
|
|
|
|
|
|
|
|
|
|
Classe de 5éme : Aire de la surface latérale : Soit : l’aire d’un carré égal : L’aire de la surface latérale est égale à quatre
fois l’aire d’un carré soit : A =
4 ( Soit la formule : A
= 4 a² |
|
|
|
Vous pouvez en trouver d’autres ! |
|
|
|
|
|
|
|
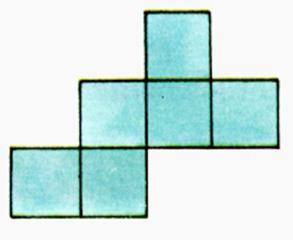
exemple 1
|
|
|
|
exemple
2 |
|
|
|
|
|
|
|
|
|
|
|
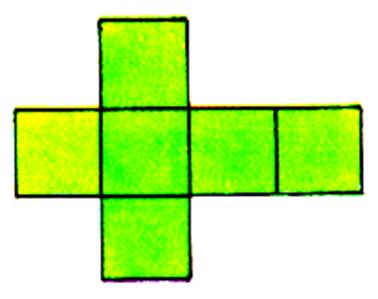
exemple
3 |
|
|
|
|
|
|
|
Attention ne pas confondre « aire totale des faces »
et « aire latérale » |
|
|
|
|
|
|
|
TRAVAUX AUTO FORMATIFS. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
CONTROLE : Donner la
définition d’un cube : 1
)
Tracer le développer d’un carré
2°) Construire un cube de carton semblable
au modèle ci
dessous.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|