|
|
|
|
|
|
|
Géométrie : le rectangle |
|
ENVIRONNEMENT du dossier:
|
2°) les diagonales dans le prisme . |
DOSSIER « géométrie » :
Cours : L e développement du
PARALLELLEPIPEDE RECTANGLE ( pavé)
|
TEST |
COURS |
|
COURS
TRAVAUX PRATIQUES
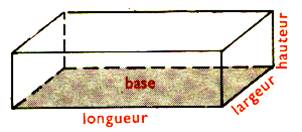
Observons l’emballage d’une
lessive :
Nous avons déjà vu
que le paquet de lessive occupe une certaine place . C’est un
« volume
|
|
|
SUITE :
|
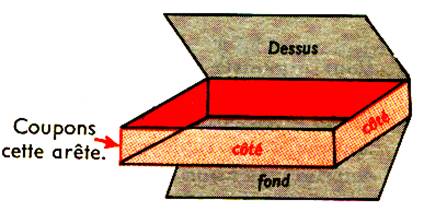
A l’aide d’un
canif , fendons le paquet suivant les
trois arêtes rouge . Nous coupons de
même la face opposée. |
|
|
Nous avons coupé
les deux le dessus et le fond sur
trois arêtes . Coupons une 7e arête
comme l’indique le croquis. |
|
|
Nous développons
et posons à plat les 6 faces.
|
La figure obtenue
s'appelle le "patron" du parallélépipède .
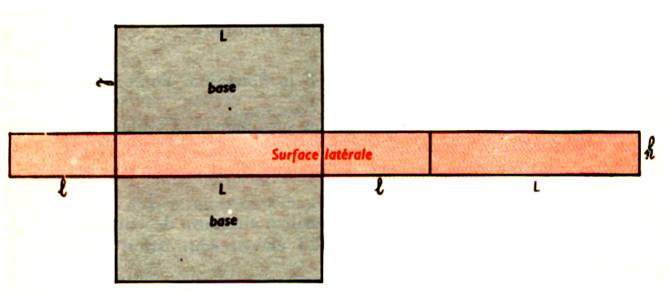
a) les
4 côtés de la boîte forment « la surface latérale » du
parallélépipède .( les murs verticaux
d’une salle de classe )
b)
Les deux autres côtés sont les bases . ( le plafond et le sol de la salle de classe )
Questions :
Quelle figure géométrique forment les
côtés étalés. ? un rectangle
A quelle dimension de ce
parallélépipède correspond la largeur de cette figure ? « h »
A quelle dimension de ce
parallélépipède correspond la longueur
de cette figure ?
(
l + L + l + L ) est représente le
périmètre de la base .
CALCULS :
Surface latérale du
parallélépipède
La surface latérale du parallélépipède
= Périmètre de base ![]() hauteur
hauteur
Surface totale du
parallélépipède :
La surface totale du
parallélépipède = Surface latérale
+ surface des deux bases.
ACTIVITES CALCULS :
1A recopier et
compléter :
|
Hauteur |
1,5 m |
55mm |
2 dm |
4 m |
2,75 m |
|
Longueur |
3m |
90 mm |
8,5 dm |
8,40 m |
0,65 |
|
Largeur |
2m |
22 mm |
4,5 dm |
|
0,50m |
|
Périmètre de base |
|
|
|
26m |
|
|
Surface latérale |
|
|
|
|
|
|
Surface de base |
|
|
|
|
|
|
Surface totale |
|
|
|
|
|
Voir le Corrigé à la
fin du cours !!!
TRAVAUX AUTO FORMATIFS.
CONTROLE :
Compléter
les phrases suivantes ( en vous aidant du cours) :
EVALUATION
ACTIVITES CALCULS :
1°) Reproduire
le tableau :
|
Hauteur |
1,5
m |
55mm |
2
dm |
4
m |
2,75
m |
|
Longueur |
3m |
90
mm |
8,5
dm |
8,40
m |
0,65 |
|
Largeur |
2m |
22
mm |
4,5
dm |
|
0,50m |
|
Périmètre de base |
|
|
|
26m |
|
|
Surface latérale |
|
|
|
|
|
|
Surface de base |
|
|
|
|
|
|
Surface totale |
|
|
|
|
|
2°) Dessiner le développement d’une boîte sans
couvercle de 4 cm de haut , 8 cm de long
et 5 cm de large .
Découper et assembler en collant sur chaque arête
un ruban adhésif .
Calculer la surface du papier utilisé .
3°) Une chambre mesure 5,10 m de long , 3,70 m de large et 2,50 m de
haut . Les ouvertures occupent une
surface de 8,40 m2 . On peint les murs de cette pièce . Quelle est
la surface à peindre ?
Le peintre donne deux couches et demande 18 € du mètre carré de chaque couche. A combien
revient la peinture de la chambre ?
4°)Une chambre mesure 5,10 m de long , 3,70 m de large et 2,50 m de
haut . On tapisse les murs de cette
pièce ; les rouleaux font 10m de long et 0,52cm de large ; Combien
faudra - t-il acheter de
rouleaux si l’on couvrait toutes les parois de cette pièce ? la plinthe
fait 10 cm de hauteur.
Combien faudra - t-il acheter de rouleaux si l’on couvrait
toutes les parois de cette pièce ? ( les
ouvertures consommeraient 2 rouleaux si on devait les recouvrir ).
1)
Calculer,
en cm², l’aire totale d’un gros dé carré de 30 cm d’arête.
2)
L’aire
totale des faces d’un cube est de 486 cm². Calculer l’aire d’une face et la mesure
de l’arête de ce cube.
3)
Papa
veut fabriquer un bac à fleurs cubique dont l’arête sera de 45 cm. Calculer le
prix du bois nécessaire à 150 € le m²
(au centime par excès).
4)
Un
peintre repeint une arrière-cuisine (murs et plafonds) de forme cubique de 2,50
m d’arête. Calculer le prix de revient, sachant : - qu’il y a une porte
d’accès de 1,50 m² ; - qu’il faut un pot de peinture à 95 € pour 17
m² ; que le peintre passe deux couches et prend 40 € de main-d’œuvre.
5)
On
enduit jusqu’à mi-hauteur une fosse de forme cubique de 7 m d’arête, d’un
produit imperméable coûtant 35 € le m².
A combien revient l’imperméabilisation de cette fosse ?
6)
A
combien revient un aquarium ayant les dimensions suivantes : L : 0,75
m ; l : 0,40 m ; H : 0,45, si le verre est vendu 235 € le
m² et si le coût de la main-d’œuvre pour l’assemblage est estimé à 350 €
? (Au centime par excès).
7)
Papa
vernit un grand coffre à jouets de 1,20 m de longueur, 0,80 m de largeur et
0,60 m de hauteur. Combien de pots seront nécessaires s’il faut un pot pour
vernir 1,5 m² ?
8)
Un
fabricant vend des cartons de 3 tailles qui correspondent aux dimensions
suivantes : - taille 1 : L : 0,25 m ; l : 0,10
m ; H : 0,12 m ; - taille 2 : L : 0,45 m ;
l : 0,25 m ; H : 0,20 m ; - taille 3 : L : 0,80
m ; l : 0,60 m ; H : 0,40 m. Le m² de carton est vendu 4,50
F. Calculer ce que gagne le fabricant s’il vend 253 cartons de taille 1, 400
cartons de taille 2 et 167 cartons de taille 3 (au centime par excès).
°Corrigé
cours : « Reproduire le
tableau : et refaire les calculs »
|
|
|||||
|
Hauteur |
1,5 m |
55mm |
2 dm |
4 m |
2,75 m |
|
Longueur |
3m |
90 mm |
8,5 dm |
8,40 m |
0,65 |
|
Largeur |
2m |
22 mm |
4,5 dm |
4,60 |
0,50m |
|
Périmètre de base |
10 m |
224 mm |
26dm |
26m |
2,30m |
|
Surface latérale |
15 m2 |
12320mm2 |
52 dm2 |
108 m2 |
6,325m2 |
|
Surface de base |
6 m2 |
1980 mm2 |
38,25 dm2 |
38,64 m2 |
0,25 m2 |
|
Surface totale |
27 m2 |
16280 mm2 |
128,5d m2 |
185,28 m2 |
6,825 m2 |