PRE REQUIS :
|
|
Lecture : 1°) @ détermination d’un point info |
|
|
1°) |
Mesure algébrique d’un bipoint. |
|
|
2°) |
Les repères cartésiens |
|
|
3°) |
Informations et conventions |
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
1°) Etude d’une
fonction (généralités) niv .V |
Tableau |
DOSSIER:LES ETUDES
DE FONCTIONS (notions et
généralités)
|
CHAPITRES : |
|
|
q |
|
q |
|
q |
|
q |
|
q |
|
q |
|
q |
|
q |
|
q |
|
q |
En mathématique on « ETUDIE UNE
FONCTION » :
Par
définition :
Etudier une fonction, c’est voir dans quels intervalles cette
fonction est croissante, décroissante ou constante.
Lectures :
|
Objectifs suivants Objectif suivant
Objectif suivant Objectif suivant |
|
||
|
Les pré
requis : |
|||
Pré requis :
calculs numérique et
algébrique.
|
|
||
|
Pré requis : placer un point et
tracé une droite ou courbe dans
un repère cartésien . |
|
||
|
|
|||
|
Informations et conventions |
|
||
|
Lecture : premières approches sur
les notions sur la « FONCTION ». |
|
||
SUITE :
|
La
FONCTION et APPLICATION ( définition) |
|
|
La
FONCTION (Généralités sur ses
modes de représentation) |
|
|
|
|
|
|
|
|
FONCTION
MODELES (graphique) |
|
|
FONCTION
linéaire |
|
|
FONCTION affine
N°2 |
|
|
FONCTION du second degré(BEP/
bac prof.) |
|
|
|
|
|
|
1-
INTRODUCTION :
De nombreuses données numériques, c 'est à dire
« chiffrables » , évoluent en fonction d' autres données , elles -
mêmes chiffrables . Il n 'est pour s ' en convaincre que de se tourner vers
quelques - unes de nos préoccupations habituelles.
Dans la vie quotidienne :
C 'est ainsi que la majorité des hommes et femmes , soucieux aujourd ' hui de l ' harmonie de leur silhouette , savent
pertinemment que leur poids en kilogramme est fonction de la quantité de
calories consommées au cours des repas
quotidiens , mais aussi de leur mode de vie ( actif ou sédentaire )..
De la même façon
, nous savons que la taille et le poids d ' un enfant évoluent en
fonction de son âge . Toutefois , il n ' existe pas de
lien absolu entre âge et taille et poids
, car d ' autres éléments non mesurables interviennent dans le phénomène de
croissance ( taille des parents , hygiène , niveau de vie , climat ….).
Il est vrai aussi que la pression
artérielle est , chez un être
humain , fonction de son âge , de
son sexe , mais encore de sa façon de s 'alimenter ,, de la quantité de cigarettes fumées et d ' alcool
consommé chaque jour , mais également de son métier et d ' autres facteurs tels
que l ' hérédité ou le tempérament individuel.
Dans l '
industrie.
Dans un autre domaine , celui de la construction automobile , il est devenu
habituel de présenter comme argument de vente la consommation d ' essence des
voitures proposées , consommation qui évolue en fonction de la puissance du
véhicule , de la vitesse , mais aussi du style de conduite de chacun et des
conditions de circulation ( sur route , en ville , par temps sec ou humide ,
etc….. …..)
Le poids des variables
A travers chacun des
exemples précédents , on voit bien qu 'une certaine quantité ( poids , taille , pression
du sang dans les artères , consommation d'essence ) varie en fonction
d' une ou de plusieurs données (
alimentation , âge , mode de vie , vitesse ) que l' on appelle des variables .
En effet , la variation de l 'une
de ces données entraîne immédiatement une variation de la quantité
étudiée .
Pour étudier cette variation , on procède par sondages ou par
mesures successives que l' on regroupe dans un tableau. On peut aussi placer
des points dans un repère .
Pour l ' abscisse , on prendra une valeur de la
variable et , pour ordonnée , la valeur prise par la quantité étudiée pour
cette valeur de la variable. On trace ensuite une courbe passant par ces
points. Elle représente la variation de la quantité en fonction des
valeurs prises par la variable.
Le mot "fonction"
utilisé dans le cours de mathématiques pourra être plus facilement assimilé si l 'on se réfère aux
définitions suivantes que donne le "Petit Larousse illustré" :
Etre fonction de: dépendre de …
En fonction de ( locution prépositive) : en suivant les variations de ……
L 'image d ' u n nombre ( si elle existe) , par une fonction
algébrique , est un nombre qui se calcule à l 'aide des quatre opérations
usuelles.
|
@info |
2-NOTIONS
DE « VARIABLE » ET DE « FONCTION » |
|
I ) Fonction d’ une variable
Exemple 1: Prenons une barre métallique et mesurons sa longueur
à différentes températures.
Nous obtenons les résultats suivants :
|
Température. ( en
degré :°) |
0° |
20° |
30° |
40° |
50° |
|
Longueur (en m.) |
1 m |
1,000 24 |
1,00036 |
1,00048 |
1,00060 |
A chaque température correspond une longueur de la
barre bien déterminée. Nous dirons que cette longueur est « fonction »
de la température, celle - ci étant la variable.
Exemple 2 : Le 4 septembre de l’année en
cours, on a relevé à différentes heures de la journée les valeurs suivantes de
la pression atmosphérique (évaluée en millimètre de mercure).
|
Heure(h) |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
Pression. |
|
752mm |
|
|
|
|
|
A chaque heure correspond une pression bien
déterminée. Nous dirons que la pression atmosphérique est fonction du temps,
celui-ci étant la variable.
Autres exemples : De même , le volume occupé
par une certaine masse gazeuse est une
fonction de sa pression, la longueur du cercle est une fonction du rayon, la
surface et le volume d’une sphère sont des fonctions de son rayon , …..etc.
Définition. Les
exemples précédents nous conduisent à la
définition suivante :
On dit qu’une grandeur
(@) est
« FONCTION » d’une autre grandeur lorsque pour chaque valeur de la
seconde on peut déterminer la valeur correspondante de la première.
EXEMPLE ABSTRAIT.
Considérons maintenant l’expression :
y = 2 x² - 5
A chaque valeur donnée à « x » correspond
une valeur bien déterminée pour « y ».
|
Par exemple |
pour
« x » = - 2,5 |
y = 7,5 |
|
|
pour
« x » = -2 |
y = 3 |
|
|
pour
« x » = - 1 |
y = -3 |
|
|
pour
« x » = 0 |
y = -5 |
|
|
pour
« x » = 1 |
y = -3 |
|
|
pour
« x » = 2 |
y = 3 |
|
|
pour
« x » = 2,5 |
y = 7,5 |
On
remarque qu’ à une valeur de « x » correspond une valeur de
« y ».
Nous dirons que l’expression « y = 2 x²
-5 » est fonction de la variable « x ».
Plus généralement :
On dit qu’une expression « y » est
« fonction de la variable « x » » lorsque, connaissant
« x » , on peut calculer la valeur correspondante de « y ».
« x » s’appelle variable indépendante ,
« y » est la fonction.
On représente souvent une fonction d’une variable
« x » par la notation f (x) et par f (a) la valeur de cette fonction pour « x
= a » .
La
correspondance entre « x » et « y » peut être
établie :
1°) Par une relation algébrique
Ainsi , dans l’exemple précédent on écrira :
Une valeur attribuée à « x » correspond pour « y » la valeur
numérique du polynôme : 2 x² - 5 ; Les opérations à faire sont toujours
possibles.
On dit que « y » est une fonction définie
pour toutes les valeurs de « x ».
Exemple 1 :
|
Soit y = 2 x² - 5 |
La variable étant « x » alors |
f (x) = 2 x² - 5 |
|
|
pour
« x » = - 2,5 |
f (-2,5)
; y = 7,5 |
|
|
pour
« x » = -2 |
f (-2)
; y = 3 |
|
|
pour
« x » = - 1 |
f (-1)
; y = -3 |
|
|
pour
« x » = 0 |
f ( 0 )
; y = -5 |
|
|
pour
« x » = 1 |
f ( 1 )
; y = -3 |
|
|
pour
« x » = 2 |
f ( 2)
; y = 3 |
|
|
pour
« x » = 2,5 |
f (2,5)
; y = 7,5 |
Exemple 2 :
y = 3 x² - 5
x +1 . A une valeur attribuée à
« x » correspond pour
« y » la valeur numérique su polynôme 3 x² - 5 x +1
Exemple 3 :
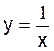est une fonction définie pour
toutes les valeurs de « x », sauf x =0 qui annule le dénominateur.
Exemple 4 : 
est une fonction
définie pour toutes les valeurs de « x » inférieures ou égale à 5.
2°) au moyen
d’une mesure (valeur expérimentale)
Une barre de cuivre étant donnée, au nombre
« x » qui repère la température, on peut faire correspondre le nombre
« y » longueur de la barre ( en mm , par exemple)
II ) Fonction de plusieurs variables
« x » et « y » étant des lettres
susceptibles de prendre diverses valeurs numériques, on dit que « z »
est une fonction de « x » et « y » si lorsque
« x » et « y » sont donnés , il leur correspond une valeur
de « z »
Exemple 1: l’aire d’un rectangle z = x
y est fonction de la longueur
« x » et de la longueur « y ».
Exemple 2 :
|
3- INTERVALLE
|
On appelle « intervalle entre le nombre
« a » et le nombre « b » » ; que l’on note
« 
» ; ( « a » et « b » étant des
nombres quelconques) tels que « a < b » , l’ensemble de tous
les nombres compris entre le nombre
« a » et le nombre
« b ».
Remarque :
sur l’intervalle des valeurs qui définissent
la fonction et les valeurs qui « ne définissent pas la
fonction. »
Il arrive que la fonction « n’existe
pas » on dit qu’elle n’est pas définie pour certaines valeurs de
« x ».Nous vous montrons deux exemples , couramment rencontrés, dans
l’étude des fonctions.
Soit la fonction
dont l’équation est y = 
. On peut calculer « y » pour n’importe qu’elle
valeur de « x » sauf pour
« x = 1 » , valeur qui annule le dénominateur. ( on ne peut
pas diviser par zéro ). Nous dirons que la fonction f(x) = . Est définie pour toutes les valeurs de « x » sauf
pour « x = 1 ».
De même, la fonction f(x) = 
n’est définie que
pour les valeurs de « x » supérieures à « 2 ». (la racine
carrée d’un nombre négatif , par définition « n’existe » pas.)
|
|
|
On dit qu’une fonction est « CROISSANTE » dans un
intervalle et ( a < b) lorsqu’en donnant à la
variable des valeurs de plus en plus
« GRANDES » de « a » à « b » , la fonction prend elle même des valeurs de plus en plus
« GRANDES ».
Si ,
dans les mêmes conditions, la fonction prend des valeurs de plus en plus
« PETITES » , on dit que la fonction est « DECROISSANTE »
dans l’intervalle
Enfin si ,
lorsque la variable croît de « a » à « b » , la fonction
conserve toujours la même valeur, on dit qu’elle est « CONSTANTE »
dans l’intervalle .
|
|
5- ETUDIER
une FONCTION. : Définition. |
|
Etudier une
fonction, c’est voir dans quels intervalles cette fonction est croissante,
décroissante ou constante.
Préambule sur
la représentation graphique d’une fonction:
A chaque étude d’une fonction de variable
« x » ; « f(x) » on fait correspondre à « x » un
calcul qui nous donne une valeur « y » telle que la valeur de f (x) = y .
Ces deux
valeurs « x » et
« y » , vont , dans le cas
d’une représentation graphique, servir à
représenter « un point particulier » dans un système d’axes (
« système »appelés couramment : repère cartésien ).
Pour
déterminer la position d’un point, on dit que l’on a besoin de ses coordonnées.
Ainsi ce système de deux droites graduées qui se coupent s’appelle
« système d’ axes de coordonnées »
|
6 -SYSTEME D’ AXES DE COORDONNEES |
|
.
AXES DE
COORDONNEES.
|
|
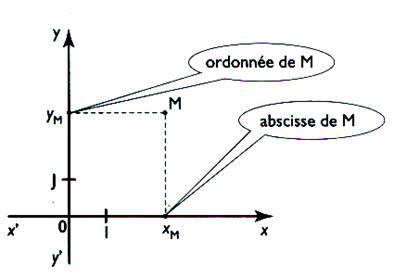
Pour repérer la position d’un point dans un plan,
on construit deux axes rectangulaires (perpendiculaires) « x ’x »
et « y’ y » et , sur ces deux axes, on prend comme origine leur point
de rencontre « O ». « x’ x » s’appelle « axe
des abscisses » ou « axe des x » et
« y’ y » est appelé « axe des ordonnées » ou « axe des y ». |
= x
s’appelle ABSCISSE du point M .
= y
s’appelle ORDONNE du point M .
x et y sont
les coordonnés du point « M ».
O est l’
ORIGINE DES COORDONNEES
Il est bien
évident que , les axes ayant été choisis, un point « M » a un système
de coordonnées et un seul, et que , réciproquement, deux nombres étant donnés ,
il existe un point et un seul qui a pour abscisse le premier et pour ordonnée
le second.
On exprime ce
résultat en disant : un point est déterminé par ses deux coordonnées.
|
|
= x s’appelle ABSCISSE du point M . = y s’appelle ORDONNE du point M . |
CAS
PARTICULIERS :
1°) Si
« M » est sur l’axe « x’ x » ; y M est en « O ». Donc ,
pour tous les points de l’axe des « x » on a « y = 0 »
2°) si « M » est sur l’axe des « y’
y », x M est en O . Donc , pour tous les points de
l’axe « y », on a : x =
0
|
|
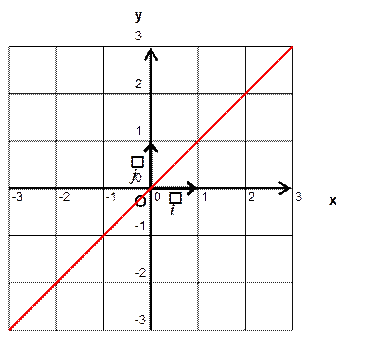
Si y = x La droite
est la bissectrice de l’angle
droit : . Pour un point M quelconque de la
droite : x M = y M Cette droite est dite aussi : première
bissectrice des axes. |
|
|
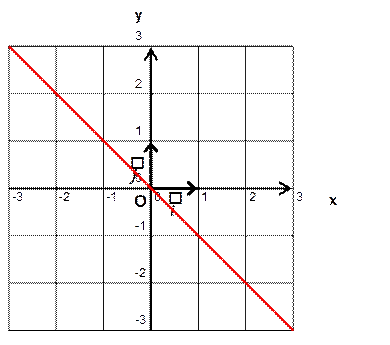
Si y = - x
La droite
est la bissectrice de l’angle
droit :. Pour un point M quelconque de la
droite : y M = - x M Cette droite est dite aussi : deuxième
bissectrice des axes. |
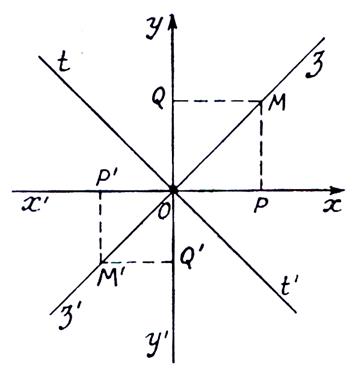
Remarques :
|
|
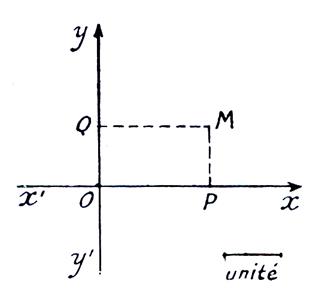
Les
droites « z z’ » et
« tt’ » sont les diagonales
du repère .
Pour tout point de « z z’ » on a
MP = MQ et MQ = PM ; donc OP = OQ %ºSi M est sur la demi - droite Oz , et sont positifs , donc = c’est à dire que « x =
y » %ºSi M’ est sur la demi -droite Oz’ , et sont négatifs et on a encore = c’est à dire « x =
y » %º Donc, tous
les points de la bissectrice « z’ z » des axes , on a
« x = y » On verra de même que pour tous les points de
« t t’ » de
l’angle : x=-y |
|
6- COORDONNEES
DU MILIEU D’ UN SEGMENT. |
|
|
|
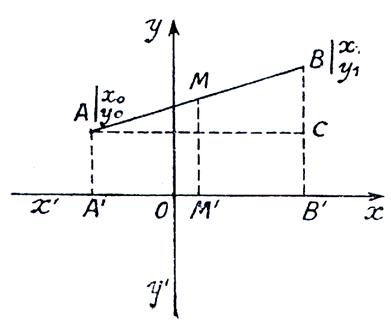
Soient A et B deux points ayant respectivement
pour coordonnées x O et y O et x1 et y1 , A’ et B’ leurs projections sur
l’axe des « x » . Soit « M » le milieu de A B ,
« x » et « y » ses
coordonnées et « M’ » sa projection sur « x ‘ x » . |
« M’ » étant le milieu de A’ B’ , son abscisse
(qui est la même que celle de M) est égale à x=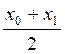 
On démontrera
de même que son ordonnée
« y » =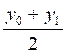 
On en conclut que les coordonnées
du point « M » sont donc :
|
|
x= |
|
y = |
|
|
7- DISTANCE
DE DEUX POINTS |
Proposons nous
de calculer la distance des deux points
« A » et « B » de la figure précédente. Pour cela ,
menons par « A » la parallèle à « x’ x » . Cette droite coupe « B B’ »en
un point « C ».
Dans le
triangle « ABC » on a :
= +
or A C =
A’ B’ et
= - = x1 - x 0
Donc =
On démontrera
de même que BC =
Donc :
|
|
AB² =( x1 - x 0 )² + ( y1 - y 0
)² |
|
|
@ info |
8 - APPLICATION : EQUATION D’UN CERCLE |
|
|
|
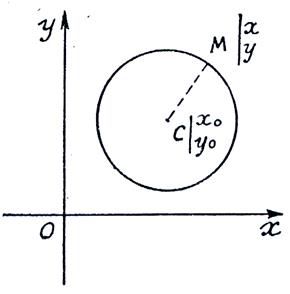
Soient deux
axes de coordonnées « O x »
et « O y » et un cercle de rayon « R » dont le centre
« C » a pour coordonnées
« x0 »
et « y0 ». |
Pour
qu’ »un point « M » de coordonnées « x ; y » soit
sur le cercle il faut et il suffit que
« CM = R » ,
R sur « x » = x M
- x C et R sur « y » = ( y M - y C)
Comme « x M = x
et xC = xO »
et « yM
= y et yC
= yO »
ce qui nous donne
, en utilisant le résultat de l’exercice précédent.
(1)
R ² = ( x - xO
)² + ( y - yO )²
Soit R =
La relation
(1) : R ² = ( x - xO
)² + ( y - yO )² s’appelle « l’équation du cercle
C », si :
1°)
Les coordonnées de tous les points de « C » vérifient cette relation,
2°)
réciproquement, tout point dont les coordonnées satisfont à cette relation est
sur « C ».
|
9 - REPRESENTAION GRAPHIQUE DE LA VARIATION D’UNE
FONCTION. |
|
Lorsqu’une
grandeur « x » est fonction
d’une autre « y » , à chaque valeur de la variable
« x » correspond une valeur
« y » de la fonction.
On dit que
« x » a pour image
« y » est on le
note : x y
· « a pour image » se symbolise par la flèche à talon :
Afin de voir
aisément comment varie la fonction lorsqu ‘on
donne à la variable différentes valeurs, on traduit les résultats en utilisant
deux axes de coordonnées « x’ x » et « y’ y »
A chaque valeur « x O »
de la variable correspond une valeur « y O = f (x0)
» de la fonction.
|
|
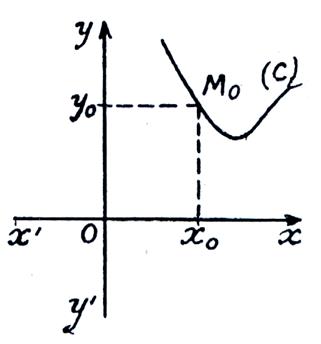
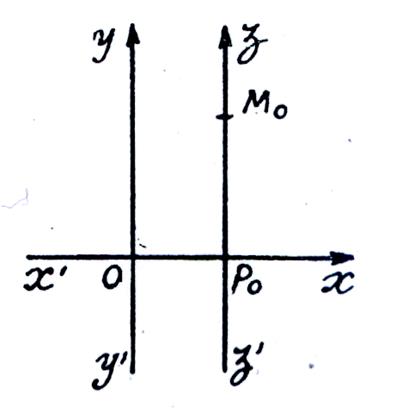
Construisons
le point « MO » qui a pour abscisse « x O » et pour ordonnée « yO ».
Lorsque « xO » varie en
prenant toutes les valeurs possibles , le point MO se
déplace ; il décrit une ligne « C » qu’on appelle
« courbe représentative » de la variation de la fonction ( ou
« graphique » de la fonction) |
Remarque sur la
procédure de construction d’un point dans le repère :
|
|
Remarquons que pour construire le point MO
on peut construire le point « PO » de l’axe des
« x » tel que = x O , puis mener par PO la parallèle « z’ z » à « y’ y » et
, ayant orienté cette droite dans le même sens que « y’ y » , prendre sur l’axe « z’ z »
ainsi obtenu le point MO
tel que = yO = f(xO). |
Dans certains cas, il est possible de démontrer que
la courbe représentative de la variation d’une fonction est une ligne étudiée
en géométrie. Dans ce cas son tracé est immédiat.
Sinon , l’étude de la variation de la fonction
permet d’en construire un tracé
« approximatif » qu’on précise en cherchant quelques points ,
notamment les points de rencontre avec les axes.
|
10 - « L’INFINI » mathématique |
@ info |
Au cours de
notre étude des fonctions,nous
emploierons souvent les
expressions : « l’infiniment grand» ; « l’infiniment petit » , ou de façon abrégée
« l’infini »
Que signifie ces mots ?
Tout d’abord il est clair qu’on peut toujours
augmenter un nombre donné, allonger une droite donnée. Considérons donc une grandeur et faisons croître sa valeur absolue ,
de telle façon qu’elle soit toujours supérieure à une quantité qu’on pourra
nous assigner , aussi grande soit telle.
Nous appellerons cette valeur, « numériquement indéfinissable » ,
l’infiniment grand et nous la représenterons par le symbole : ∞.
(ressemble à un huit couché )
De même nous définirons « l’infiniment
petit » comme une grandeur décroissante , inférieure en valeur absolue à
toute quantité donnée aussi petite soit elle et nous
la représenterons par le symbole : e
( lettre grecque appelée
« epsilon ») ;Il est à noter que l’infiniment grand et
l’infiniment petit peuvent être positifs ou négatifs. ± z.
; ± e .
Ainsi que l’ a remarqué Pascal, l’infiniment grand
et l’infiniment petit sont intimement liés
l’un à l’autre .
Considérons, par exemple, la
fonction 
en même temps que son dénominateur devient
infiniment petit , cette fraction devient « infiniment grande » , inversement elle est infiniment petite lorsque
« x » est infiniment grand.
Cette corrélation
a d’ailleurs une conséquence remarquable.
Si l’on donne a « x » deux valeurs
infiniment petites , l’une négative - e
, l’autre positive + e , et il est évident que ces deux valeurs
sont aussi voisines qu’on le veut , y devient successivement infiniment grande
et négative ; - z. ,
puis infiniment grande et positive ;
+ z. en sorte que ces deux
valeurs indéfinis se succèdent immédiatement, sans valeurs intermédiaires.