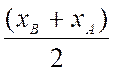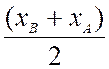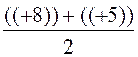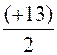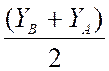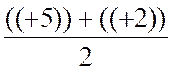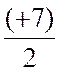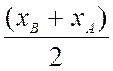Pré requis:

Projections orthogonales d'un segment dans un repère cartésien

Repères cartésiens

Segment de droites les opérations.

ENVIRONNEMENT du dossier:

Index warmaths

Objectif précédent : Milieu d’une droite

Objectif suivant : a)Centre de la symétrie centrale d’un segment. b)Liste des cours sur la fonction linéaire.

Liste des cours sur le repérage.

DOSSIER : COORDONNEES du MILIEU d'un segment dans un plan.

Info : Le milieu est la symétrie central

TEST

COURS

Devoir Contrôle

Devoir évaluation

Interdisciplinarité

Corrigé Contrôle

Corrigé évaluation

Commentaire: nous avons vu le calcul de la position du MILIEU d'un point sur une droite; on cherchait une valeur numérique.

Dans ce cours nous avons à trouver 2 valeurs numériques: une valeur représentant la position du point sur l'axe "x" , l'autre valeur représentant la position du point sur l'axe "y"

COURS:

Schéma: cas courant

Rappels sur les : Projections d’un segment dans un repère cartésien ) , le repère est dit «  cartésien ortho - normé »

y

Ay A

My

By B

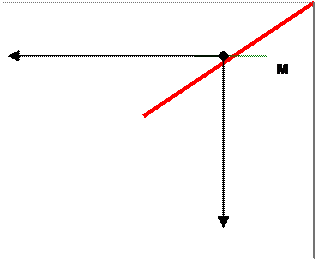
M_x

Bx Ax x

Les segments de droites AB et BA sont appelés les projetées orthogonales du segment AB .

La norme permet de graduer les axes.

Si la norme * sur et est égale « mesure » le repère est dit « normé »

*Voir [O,I] et [ O, J ]

Le point :…	à pour abscisse	à pour ordonnée	à pour coordonnées
A	xA	yA	A(xA;yA)
B	xB	yB	B(xB;yB)
M	xM	yM	M(xM;yM)

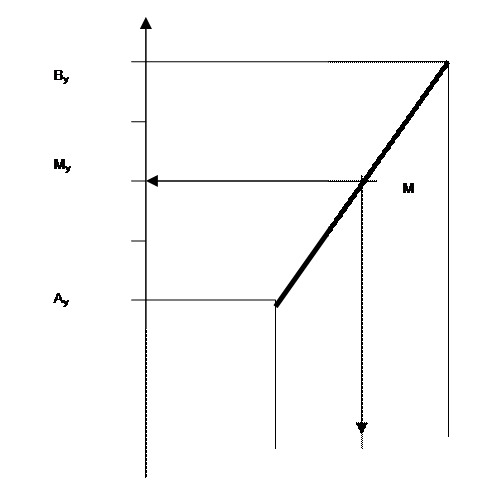
Si le Point " M " est le milieu du segment AB :

M_x est le milieu du segment A_xB_x

et

M_y est le milieu du segment A_yB_y

PROBLEME:

Quelles sont les coordonnées du milieu (M) d'un segment dans un repère cartésien Orthonormé? Sachant que A (+2;+2) et B (+5;+6)

Commentaire:

Il faut calculer la position de la projetée du point M sur l'axe des abscisses ,et calculer la position de la projetée du point M sur l'axe des ordonnées.

(l'ordre de recherche des valeurs n'a pas d'importance , ce qui est important est de respecter l'ordre des valeurs dans la conclusion , à savoir ,que par convention , la première valeur représentera toujours l'abscisse et la seconde valeur l'ordonnée): M (x_M;y_M)

I ) CALCUL de la position du point M_x ; d'abscisse x_M

Schéma:

Soit une droite graduée , un point « O » d ‘ abscisse « 0 » , un point « I » d ‘abscisse « 1 » , un point « A » d ‘abscisse « x_A » et un point « B » d ‘«  abscisse « x_B »

*

La position (x_M) du milieu ( noté M) d'un segment est égale à la somme de l'abscisse de l'extrémité (x_B )plus l'abscisse de l'origine ( x_A)du segment divisée par deux .

x_M =

Application:

Sur une droite graduée "x"; on trace un segment AB tel que A= + 5 ; et B = (+8) ; quelle est la position du point M sur la droite graduée ?

On sait que" le milieu d'un segment est égal à la somme des valeurs des extrémités" :

On peut écrire que :

x_M =

On remplace les lettres par les valeurs:

x_{M =}

x_M =

x_M =(+6,5)

Conclusion : la position du point M sur la droite graduée "x" est de (+6,5)

Vérification: prendre une graduation égale à un cm. il suffit de tracer une droite , de placer les extrémités du segment , de placer le milieu sur ce segment, et ensuite de mesurer la longueur qui sépare le point "M" de l'origine "O" de l'axe .

CALCUL de la position du point M_y ; d'abscisse y_M

Schéma:

Soit une droite graduée , un point « O » d ‘ abscisse « 0 » , un point « j » de mesure « 1 » , un point « A » nommé « y_A » et un point « B » nommé « y_B »

Les écritures :By et YB sont équivalentes , elles désignent l'ordonné du point B dans le repère cartésien. Les écritures :Ay et YA sont équivalentes , elles désignent l'ordonné du point A dans le repère cartésien.

*

Nous utiliserons la formule suivante

On sait que YA et YB sont les positions (ordonnées) des points A et B sur la droite "y"

YM =

Application:

Sur une droite graduée "y" ; on trace un segment AB tel que A= (+ 2 ) ; et B = (+5) ; quelle est l'ordonnée du point M sur?

On sait que" le milieu d'un segment est égal à la somme des valeurs des extrémités" :

On peut écrire que :

Y_{M =}

On remplace les lettres par les valeurs:

Y_{M =}

Y_{M =}

Y_M = (+3,5 )

Conclusion : la position du point M sur la droite graduée "y" est de (+3,5)

Vérification:

Il faut prendre une graduation égale à un cm. il suffit de tracer une droite , de placer les extrémités du segment , de placer le milieu sur ce segment, et ensuite de mesurer la longueur qui sépare le point "M" de l'origine "O" de l'axe .

EN RESUME:

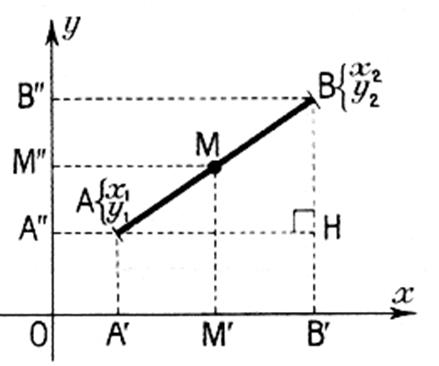
Soit M ( x ; y ) le milieu du segment AB. Ses projections M' et M" sur les axes sont les milieux respectifs de A'B' et A"B" . D'où =

Soit - = -

Alors x - x ₁ = x₂ - x ; par transformation 2x = x₁ + x₂

Donc x = 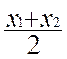; on trouverait de même y =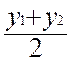

L'abscisse ( ou l'ordonnée ) du milieu d'un segment est égale à la demi- somme des abscisses ( ou des ordonnées) de ses extrémités .

Les coordonnées du milieu ( M ) d'un segment noté [AB]sont x_M et y_M avec :

xM =

yM =

REMARQUE :

	:INFO plus ++++
Le point I (x ;y) étant donné ; tout point A (xA ;yA ) a pour image dans la symétrie centrale ´ le point B tel que : Le vecteur I A = le vecteur – IB Ou le vecteur IB = le vecteur - IA

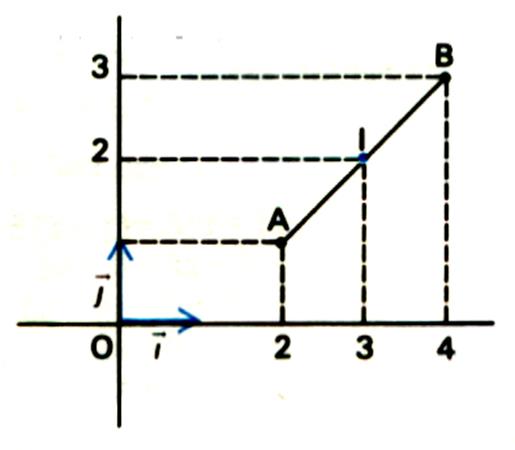
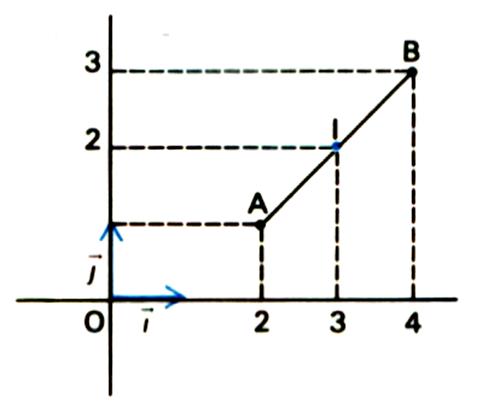
Exemple :

On considère deux points A ( +4 ; +1) et B ( +8 ;+4). Calculer la longueur de AB , les coordonnées du milieu M de AB et la longueur OM .

Calculs :

On a ² = ( 8 - 4 ) ² + ( 4- 1 ) ² = 4 ² + 3 ² = 25

Donc AB = = 5

Le milieu M de AB a pour coordonnées :

Pour x = ( 8 + 4 ) = + 6 et pour y = ( 1 + 4 ) = 2,5

Donc : OM² = 6² + 2,5 ² = 42,25 et donc OM = = 6,5

Travaux auto-formatifs.

CONTROLE :

A quoi est égal la position du milieu d'un segment dans un repère cartésien?

Donner les formules permettant de calculer la position du milieu d'un segment sur une droite graduée?

EVALUATION

1. Soit un segment AB	A(+2 ; +5 )	B ( +2 ;+7)	Coordonnées du milieu du segment AB =?
2. Soit un segment AB	A(-2 ; +5 )	B ( +2 ;-7)	Coordonnées du milieu du segment AB =?
3. Soit un segment AB	A(-2 ; -5 )	B ( -2 ;-7)	Coordonnées du milieu du segment AB =?
4. Soit un segment AB	A(+2 ; +5 )	B ( -2 ;-7)	Coordonnées du milieu du segment AB =?

INTERDISCIPLINARITE