|
Projection orthogonale d’un segment |
|
|
Pythagore |
|
|
Longueur d’un segment |
|
ENVIRONNEMENT du dossier:
|
Objectif précédent : |
Tableau |
DOSSIER :
1°) Distance de
deux points dans un repère ; dont distance
d'un point à l'origine .
2°)Calcul de la longueur d’un segment situé dans un plan .
|
TEST |
COURS |
Interdisciplinarité |
|
Rappel : Projection orthogonale d’un segment (appelé aussi repère cartésien
) ,cas courant le repère est dit
« cartésien ortho -
normé »
Les
segments de droites Ay By et
B x A x sont appelés les projetés du segment AB . La norme
permet de graduer les axes. Si la norme * sur x et y est égale « mesure » le repère
est dit « normé » *Voir
[O,I]
et [ O, J ]
![]() y
y
Ay
A

B
![]()
![]()
![]() By
By
![]()
Bx Ax x
PROCEDURE pour
obtenir la distance entre deux points dans un plan :
Pour trouver par le calcul la distance entre
les points AB , nous devons passer par les projections
sur les axes « x » et « y » .
1°) IL faut
calculer la distance des deux points projetés sur « x »
2°) IL faut
calculer la distance des deux points projetés sur « y »
les deux distances obtenues ,sont les mesures des
segments des cotés d’un triangle rectangle . (parce
que le repère est un repère cartésien orthogonal , il faut que ce repère soit « normé »).
3°) Nous en déduisons
que les deux cotés (projetée sur « x » et projetée sur « y » ) forment un angle droit , nous appliquerons le théorème
de Pythagore pour trouver la mesure du troisième segment que l’on appelle
« hypoténuse ».
Soit
un segment OE dans le plan :
CALCUL de la « distance
projetée » de deux points sur l’axe des « x »:
La distance entre
deux points est égale à la valeur absolue
de la mesure algébrique d ‘un bipoint ( d ’ origine O et d ’extrémité
E ); cette mesure algébrique est égale à
la différence de l ’ abscisse de l’extrémité ( xE )
moins l ‘ abscisse de l ’ origine du bipoint (xO).
Ce qui se traduit : ½xE
- xO ½= ½![]() ½x
½x
CALCUL de la « distance projetée » entre deux points sur l’axe des « y »:
La distance entre
deux points est égale à la valeur
absolue de la mesure algébrique d ‘un bipoint ( d ’ origine O et d ’extrémité
E ); cette mesure algébrique est égale à
la différence de l ’ abscisse de l’extrémité ( xE )
moins l ‘ abscisse de l ’ origine du bipoint (xO).
Ce qui se traduit : ½yE
- yO ½= ½![]() ½y
½y
Pour connaître la distance entre les deux points OE :on posera d'après le théorème de Pythagore ;
( 1) (½![]() ½x ) ² + (½
½x ) ² + (½![]() ½y) = ½
½y) = ½![]() ½ ²
½ ²
puisque le carré d'un nombre positif ou
négatif est un nombre positif ; on peut
aussi écrire que :
(2) ![]() x² +
x² + ![]() y²
=
y²
= ![]() ²
²
NOTA :
pour les vecteur on calculera la mesure algébrique sur les « x » et
sur les « y » afin de déterminer par le calcul le sens du vecteur . (on ne parlera pas
de valeur absolue
Voir : Composantes d’un vecteur et calcul de la NORME D’UN
VECTEUR
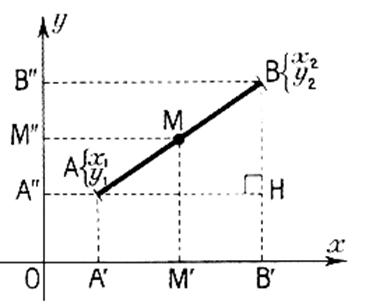
DISTANCE
de deux points A ( x1 ; y1 ) et B ( x2 ; y2)
|
Désignons par A' et B' les projections de A et B sur O
x et par A'' et B" leurs projections sur O y
. |
|
Soit H l'intersection de la droite passant par
AA" et la droite passant par BB'.
D'après Pythagore :
![]() ²
=
²
= ![]() ²
+
²
+ ![]() ² =
² = ![]() ²
+
²
+ ![]() ²
²
Or la mesure algébrique d'un vecteur porté par un axe est
égale à l'abscisse de son extrémité moins
l'abscisse de son origine . Donc
![]() = x2 - x 1 et
= x2 - x 1 et
![]() = y2 - y1
= y2 - y1
soit : ![]() ² = (x2 - x 1
) ² + (y2 - y1)²
² = (x2 - x 1
) ² + (y2 - y1)²
en particulier :
Distance d'un point à
l'origine :
la distance de l'origine O ( 0 ;0 )au point M ( x ; y ) est telle que :
![]() ² =
x² + y ²
² =
x² + y ²
soit
![]() =
=
![]() ;
;
·
![]() est toujours
positif .
est toujours
positif .
·
|
Suite
: milieu d'un segment |
ENONCE TYPE :
Soit deux points dans un plan : A (+2 ;+1 ) et B (
+7,5 ; + 5 )
Calculer
la distance entre A et B
Résolution :
I )
Calcul de la distance de la projection de AB sur l’axe des
« x »
Représentation graphique : [ xA ;
xB ]
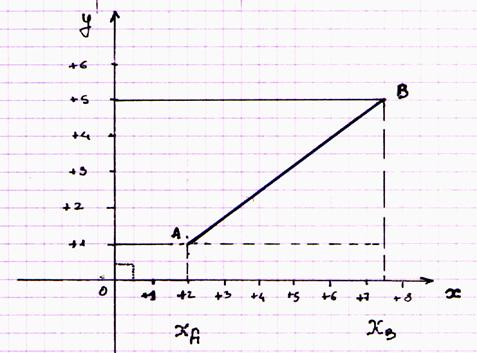
Calcul de la
distance entre xA et xB :
|
Procédure : |
Calcul de la mesure algébrique
comprise entre les deux extrémités du segment projeté des points AB sur l’axe
des « x » ; |
|
Origine du segment: |
XA = (+2) |
|
Extrémité du segment: |
XB = (+7,5) |
|
Calcul de la mesure
algébrique entre les extrémités du segment: |
XB- XA
= (+7,5) - (+2) Calcul: (+7,5) - (+2) = (+7,5) +
(-2) = (+ (7,5- 2) ) = (+5,5) |
|
Détermination de la valeur absolue du calcul
précédent : |
½(+5, 5) ½
= 5,5 |
|
Conclusion |
La distance entre A et B
sur «y » est de 5,5 |
II ) Calcul de
la distance de la projection de AB sur l’axe des « y »
Représentation graphique : [yA ;
yB ]
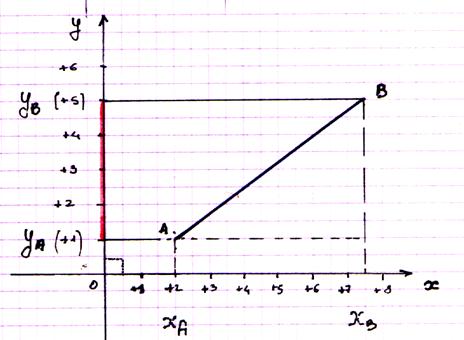
Calcul de la
distance entre yA et yB :
|
Procédure : |
Calcul de la mesure algébrique comprise entre les deux
extrémités du segment projeté des points AB sur l’axe des « y » ; |
|
Origine du segment: |
yA = ( + 1 ) |
|
Extrémité du segment: |
yB = ( + 5 ) |
|
Calcul de la mesure algébrique entre les extrémités du
segment: |
YB- yA
= (+ 5) - (+ 1) Calcul: (+ 5) - (+ 1)= (+ 5) + ( -
1) =
(+ ( 5- 1) )
= (+ 4 )
|
|
Détermination de la valeur
absolue du calcul précédent : |
½(+ 4) ½ = 4 |
|
Conclusion |
La distance entre A et B sur « y » est de 4 |
III) Calcul de la distance du
segment AB dans le plan.
D ‘ après Pythagore :
Théorème : Dans un triangle rectangle : le
« carré » de la longueur de l’hypoténuse (c’est à dire : la
longueur de l’hypoténuse multipliée par la longueur de l’hypoténuse) est égal
à la somme des « carrés » des longueurs des cotés (du triangle) formant l’angle
droit.
si l’on nomme les sommets du triangle ,
par une lettre ( A ; B ; C ) :
![]() si :
si :
AB désigne
la longueur de l’hypoténuse
AC désigne
la longueur d’un coté formant
l’angle droit
BC désigne
la longueur d’un coté formant
l’angle droit
C
On peut écrire , d’après
« Pythagore » :
AB fois AB =
AC fois AC + BC fois BC
soit : AB2 = AC 2 + BC 2
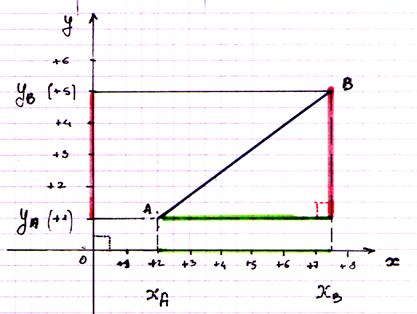
Il ne reste plus
qu’à faire l’application
numérique :
Trouver « AB » si «AC » = 5,5 et « BC » = 4 à partir de
AB2 = AC2 + BC2 ( se souvenir que ![]() =
x )
=
x )
On
pose ![]() =
= ![]()
si « a » =
30 et « b » =40 alors ![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
de
l’égalité on en tire que : le
premier membre ![]() =
AB , et le deuxième membre :
=
AB , et le deuxième membre : ![]() =
6,8 ( d’après la calculatrice
=
6,8 ( d’après la calculatrice ![]() =
6,8007353)
=
6,8007353)
on
conclut que la distance entre AB =
6 ,8
AUTRES APPLICATIONS
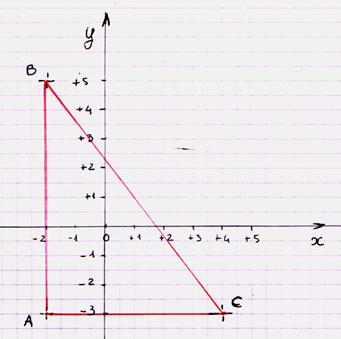
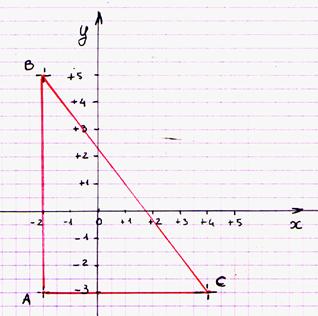
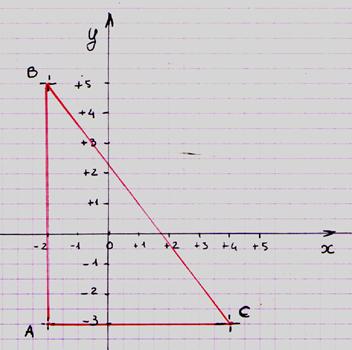
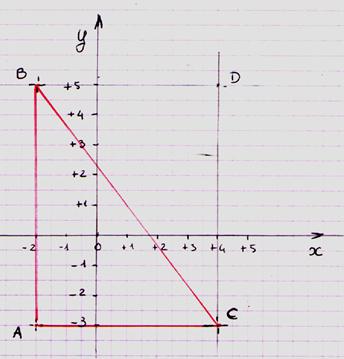
1°) Dans un repère orthonormé
( 0,![]() ,
,![]() ) ;On
place les points
A ( -2 ;-3 ) , B ( -2 ;5 ) et C ( 4 ;-3)
) ;On
place les points
A ( -2 ;-3 ) , B ( -2 ;5 ) et C ( 4 ;-3)
Question : montrez que le triangle ABC est rectangle
Résolution :
|
Remarque
:il faut que le repère soit orthogonale : ( le repère est orthonormé.) |
|
C'est le cas :
:le segment AB est parallèle à l’axe
« y » (les extrémités ont la même abscisse )
:le segment AC est
parallèle à l’axe « x » (les extrémités ont la même ordonnée )
les deux segments sont donc perpendiculaires
Il reste à montrer par le
calcul que BC est l’hypoténuse du triangle rectangle
en calculant la somme des carrés des cotés (représentés par les projetées
BD et DC)
|
|
|
Nous
avons besoin des projections de BC sur l’axe « y » et sur l’axe
« x »
La
projection de BC sur l’axe « y » est le segment DC ;
la projection de BC
sur l’axe « x » est le segment BD
TRAVAUX
AUTO FORMATIFS.
1 ) Donner la procédure permettant
d’obtenir par le calcul la longueur d’un segment (distance entre deux points )
dans un plan .
PROCEDURE pour obtenir la distance entre deux points dans un
plan :
Pour trouver par le calcul la distance entre
les points AB , nous devons passer par les projections
sur les axes « x » et « y » .
1°) IL faut
calculer la distance des deux points projetés sur « x »
2°) IL faut
calculer la distance des deux points projetés sur « y »
les deux
distances obtenues ,sont les mesures des segments des cotés d’un triangle
rectangle . (parce que le repère est un repère
cartésien orthogonal , il faut que ce repère
soit « normé »).
3°) Nous en
déduisons que les deux cotés (projetée sur « x » et projetée sur
« y » ) forment un angle droit , nous
appliquerons le théorème de Pythagore pour trouver la mesure du troisième
segment que l’on appelle « hypoténuse ».
B
I ) Soit un repère
orthonormé ( à compléter):
tracer les projections du segment
AB ; donner les coordonnées des deux points,
![]()
![]()
![]()
![]() échelle1
échelle1
Cet exercice sera repris avec Obj :
« Pythagore » ,
II ) Soit deux points dans un
plan : A (+2 ;+1 ) et
B ( +7,5 ; + 5 )
Calculer la distance entre A et B
III) Dans un repère orthonormé ( 0,![]() ,
,![]() )
)
On place les points A ( -2 ;-3 ) , B (
-2 ;5 ) et C ( 4 ;-3)
a) montrez que le triangle ABC est rectangle